自适应模拟退火算法优化离心泵水力性能设计

从离心泵能量性能计算模型中可以看出：离心泵多工况水力性能优化设计问题属于非线性、多目标求解问题，其解并不唯一。而自适应模拟退火算法（Adaptive Simulated Annea-ling，ASA）^［11-13］是在传统的模拟退火法和模拟淬火过程的基础上提出的，是一种用于解决具有多峰和非光滑性的高难度非线性优化问题。其特点是：模拟退火过程是求解目标最小值的过程，产生的解是全局最优解，且收敛速度较快。

选用ASA算法对离心泵多工况水力性能优化设计问题进行全局优化。由于离心泵多工况水力性能优化设计问题是一个最大值问题，需要将其转换成进行求解。主要求解步骤如下：

（1）算法初始化 随机产生一个初始解x₀，以x₀作为当前最优解，并计算其目标函数值。

设置初始温度T_0，j为1.0，设置初始温度变化次数k=1，并给定最大循环步数L_k。

（2）邻域搜索 首先，对当前最优解作随机扰动，通过式（2-43）、式（2-44）、式（2-45）生成新解。

式中 y^j——第j个待求参数的扰动，1≤j≤D；

u^j——介于0和1之间的随机值；

B_j——第j个待求参数可能取的最大值；

A_j——第j个待求参数可能取的最小值；

c——温度控制系数。

接着，计算新的目标函数值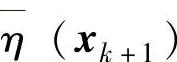，并计算目标函数值的增量（即代价函数，CostFunction）

如果Δ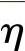＜0，则接受新产生的最优解为当前最优解；若Δ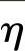＞0，则以下面的Metropolis准则来判断是否接受。

随机产生一个在［0，1］区间上均匀分布的随机数ξ，如果P＞ξ，则接受新解，否则放弃。(https://www.xing528.com)

（3）参数控制

1）退火（Annealing）：采用式（2-47）计算每次迭代的退火温度。

2）回火（Reannealing）：设置回火前接受解的次数m，即每隔m个接受解都要进行回火。

采用有限差分法计算向量x中每个变量的梯度s_j：

式中 x_opt——目前为止找到的最优解；

δ——步长；

e_j——一个维数为D的向量，第j个分量是1，其余为0。

s_j=s_max时，T_k和k需要重新设置，即

3）淬火（Quenching）：在退火过程缓慢的情况下，需要对其进行淬火处理，使其温度快速降低，即

式中 q_j——淬火因素（Quenching Factor）。

（4）算法终止判定 若连续N个新解都没有被接受，或代价函数值小于一个给定的值ε（0≤ε≤1），则输出当前解作为最优解，算法结束。