如何计算11.2公法线长度？

1.公法线长度计算公式（见表11-2）

表11-2 公法线长度计算公式

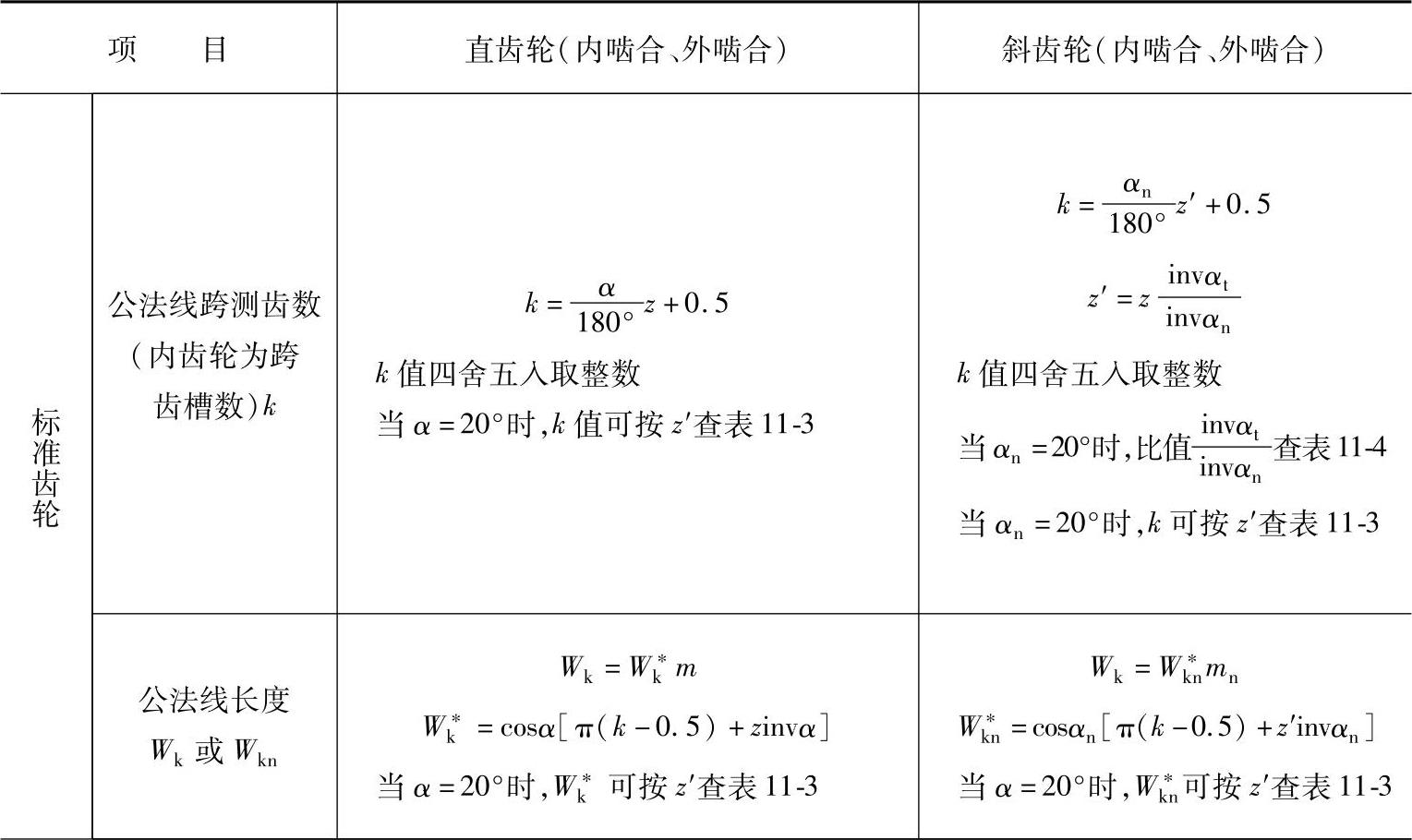
（续）

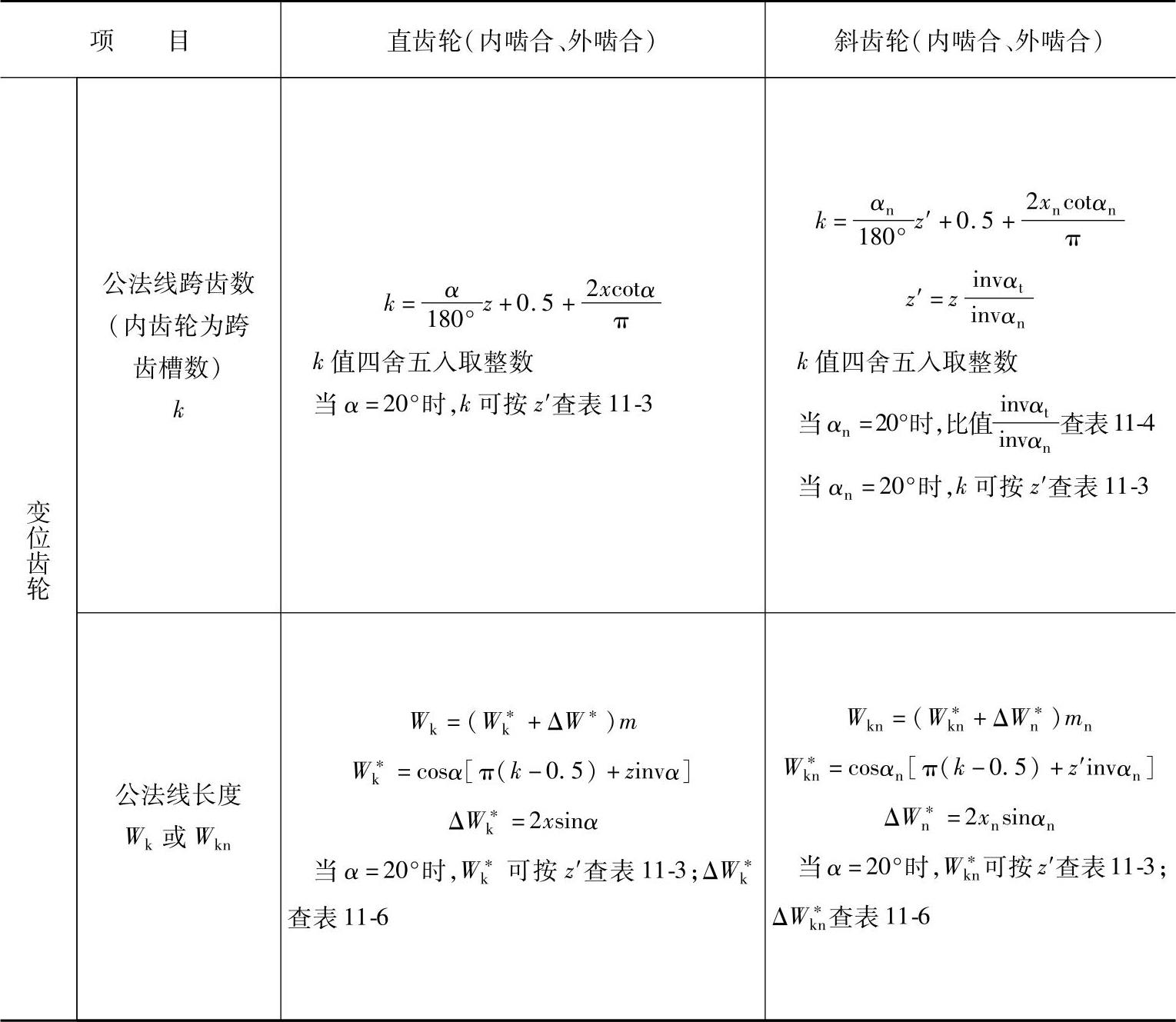
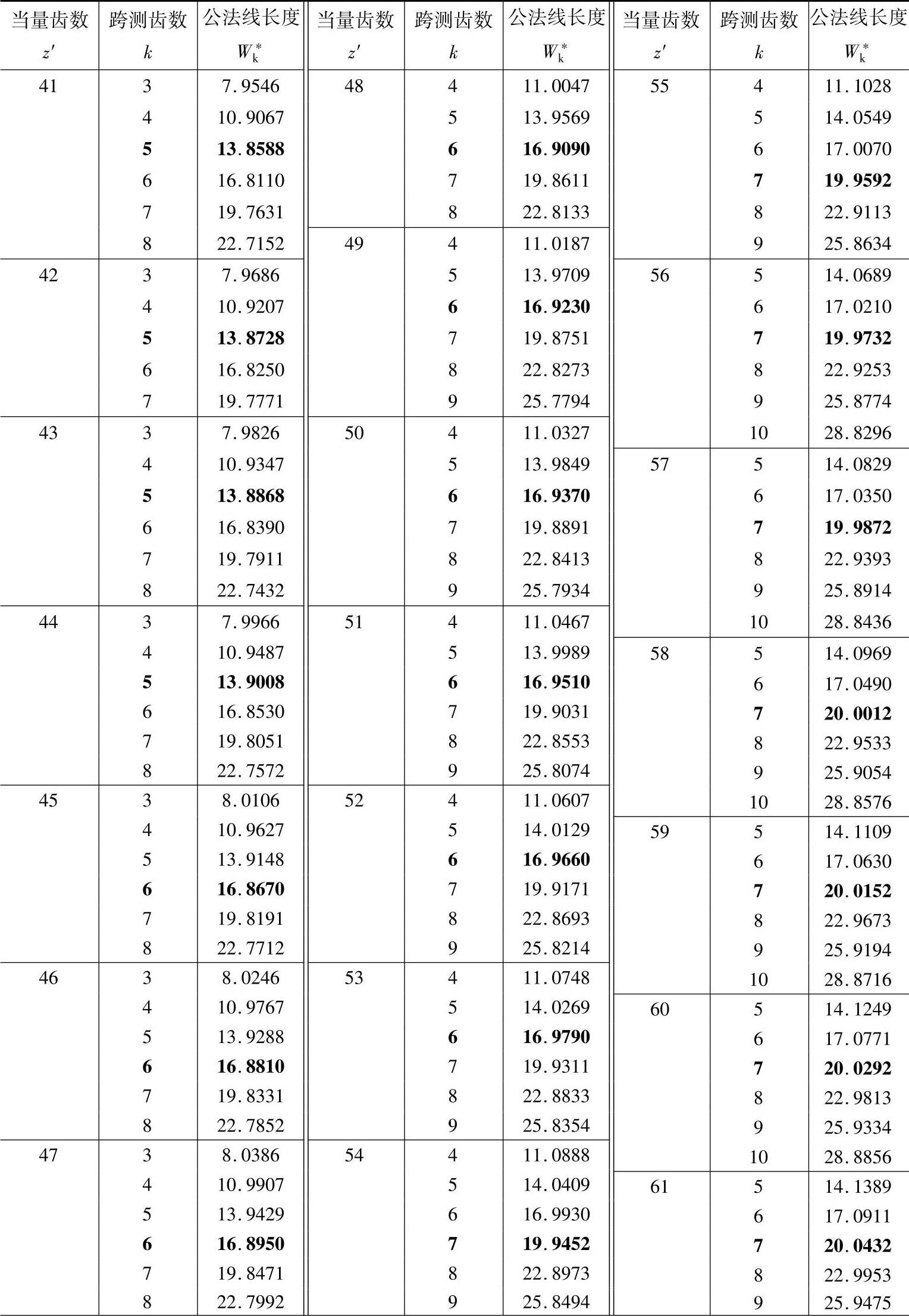
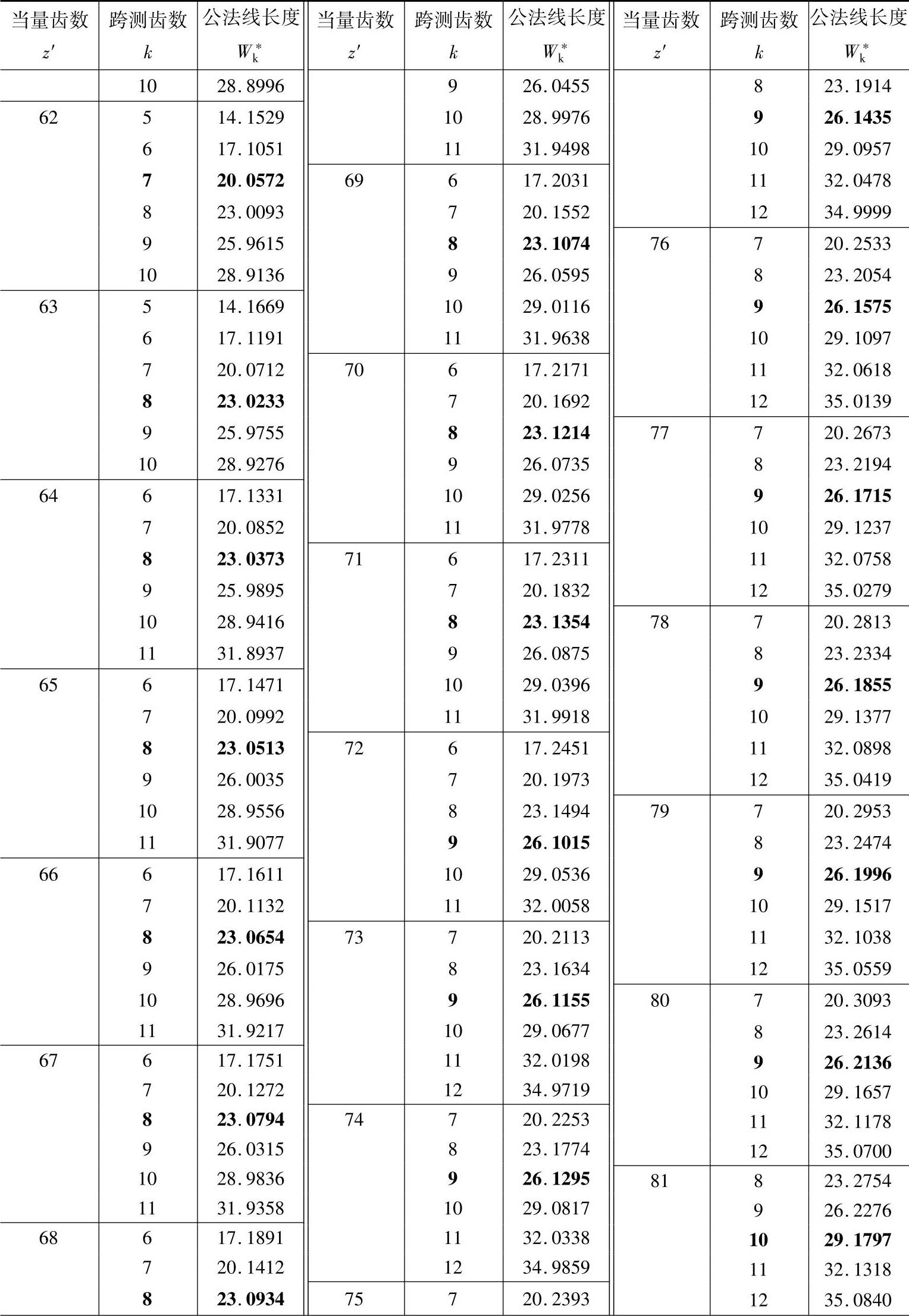
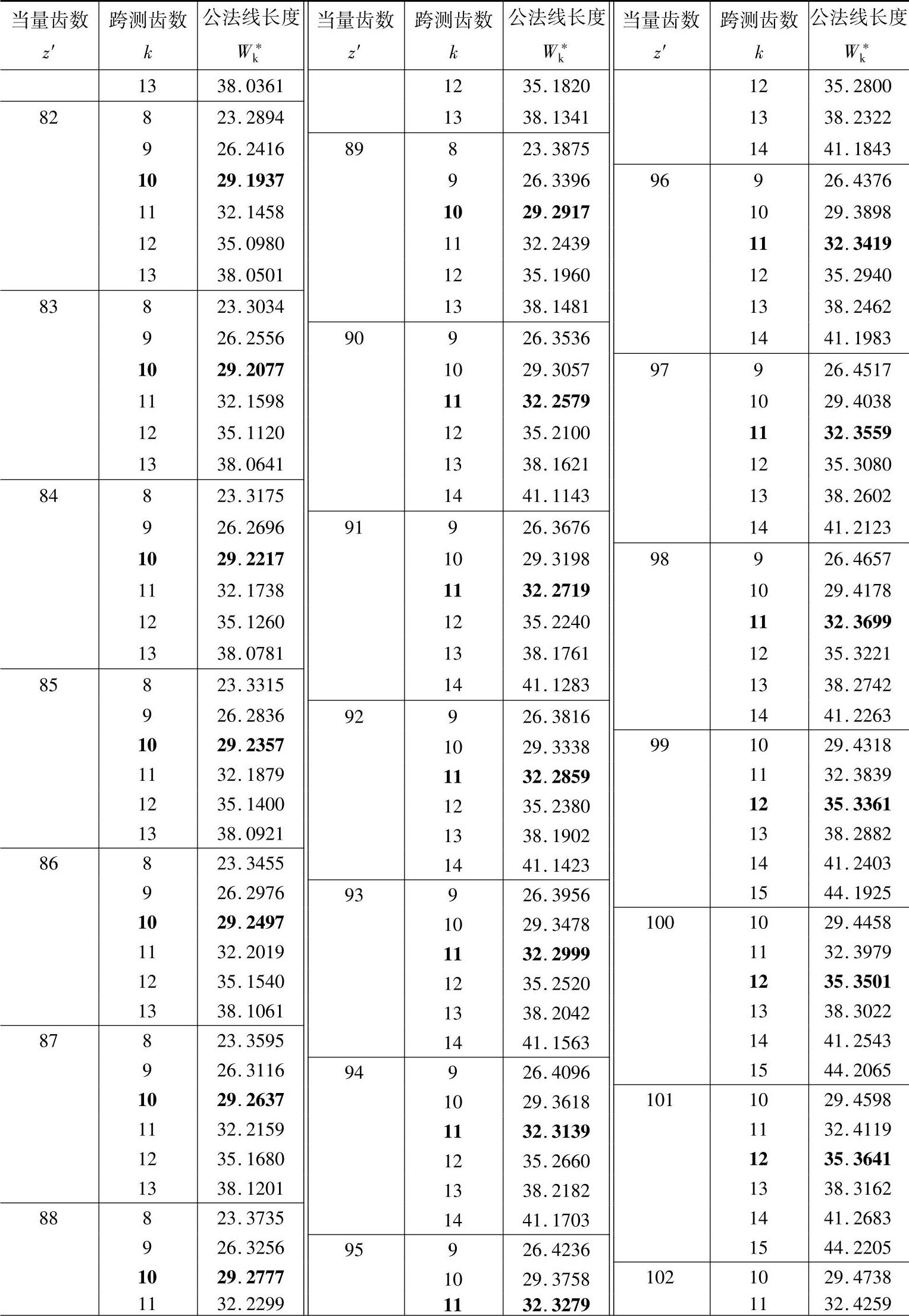
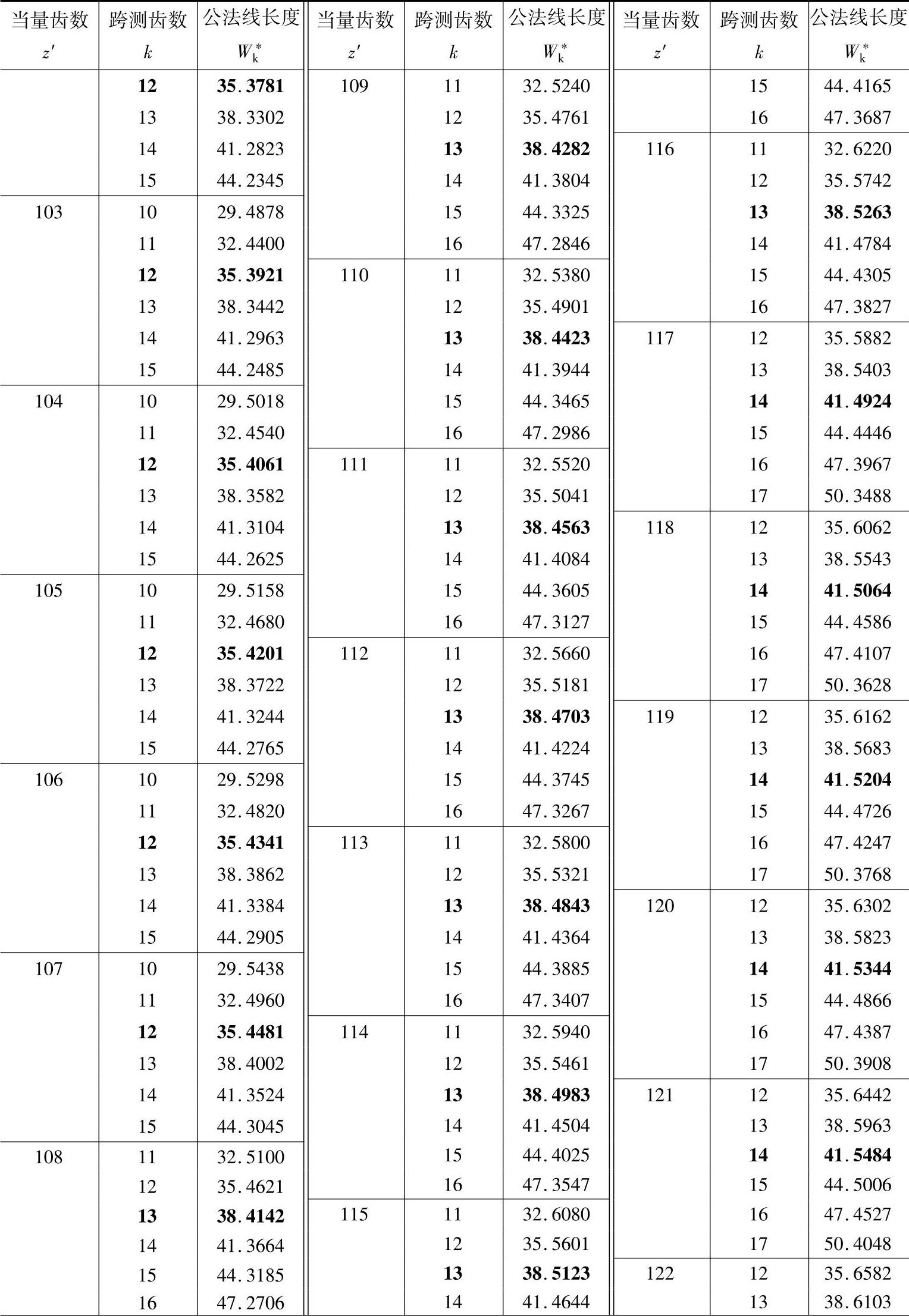
2.公法线长度计算（见表11-3）

对于斜齿轮的公法线长度计算按下例进行。

【例11-1】已知z=27、m_n=4、x_n=0.2、β=12°34′、α_n=20°，求公法线长度W_kn。

解 由表11-4查出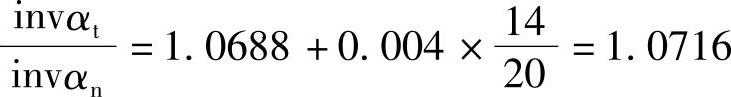，z′=1.0716×27=28.93，由表11-3查出跨测齿数k=4，由表11-3查出z′=28时的W^*_kn=10.7246mm，由表11-5查出z′=0.93时的W^*_kn=0.013mm，则

W^*_kn=10.7246mm+0.013mm=10.7376mm

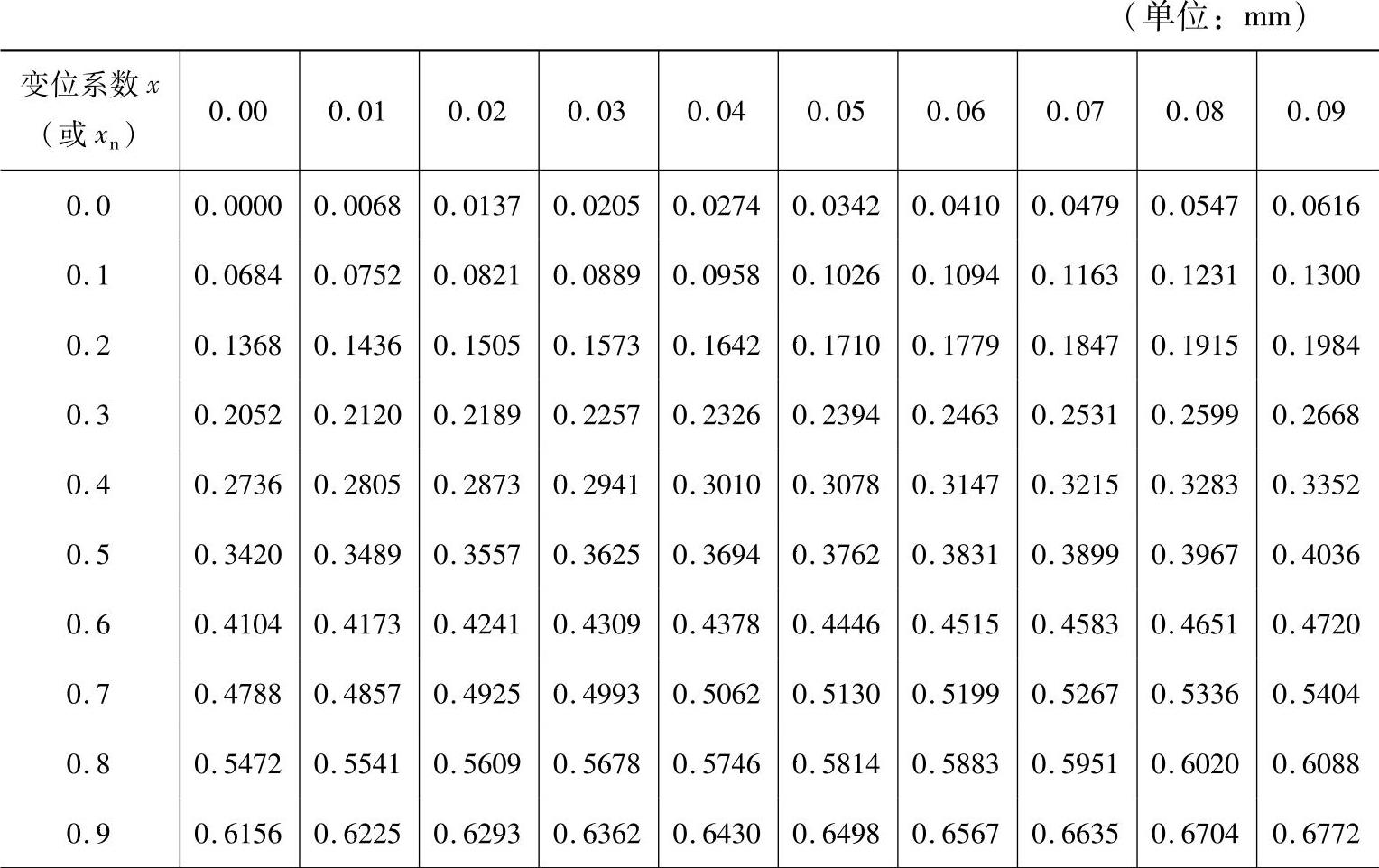
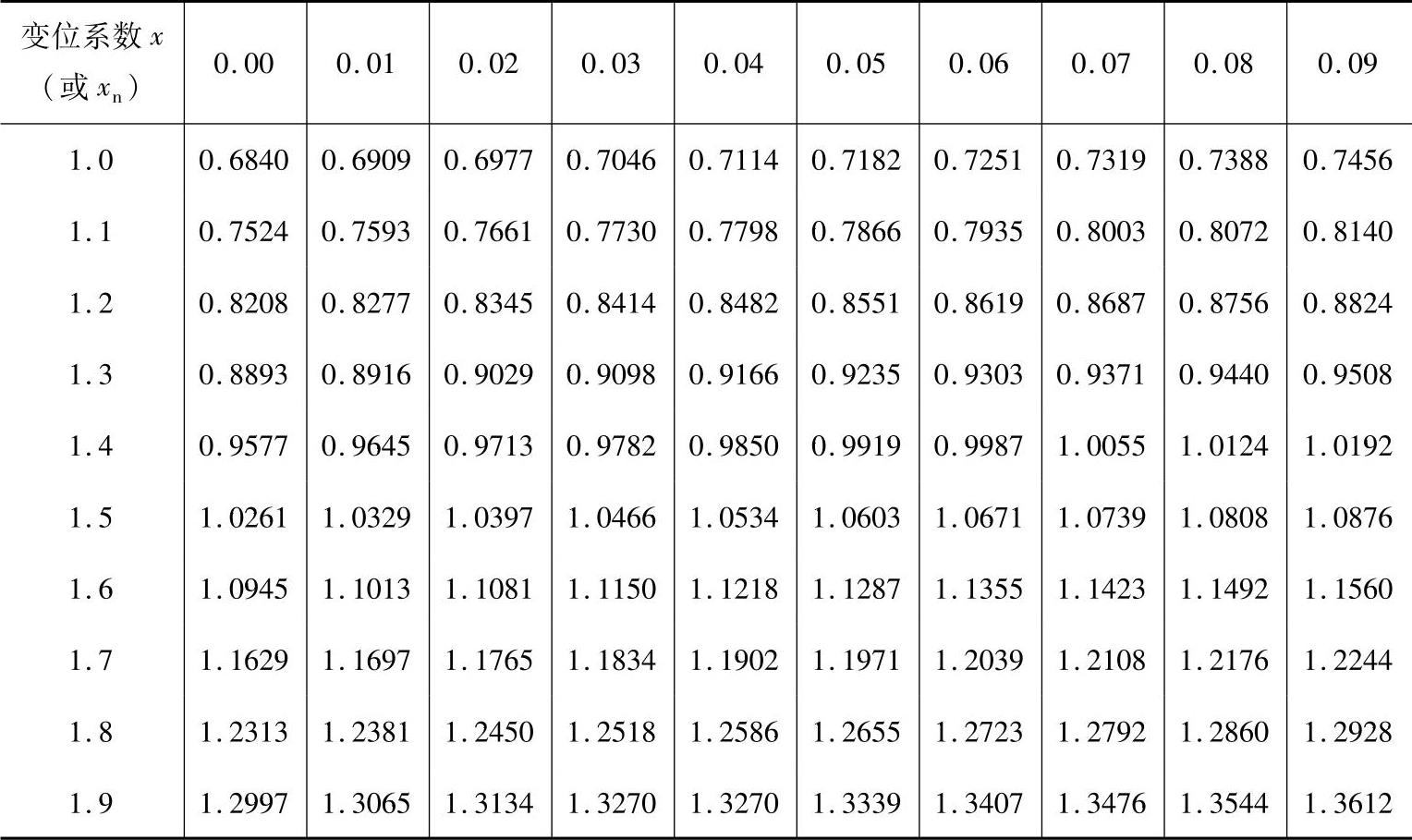
由表11-6查出ΔW^*_n=0.1368mm，则

W_kn=（10.7376+0.1368）×4mm=43.498mm

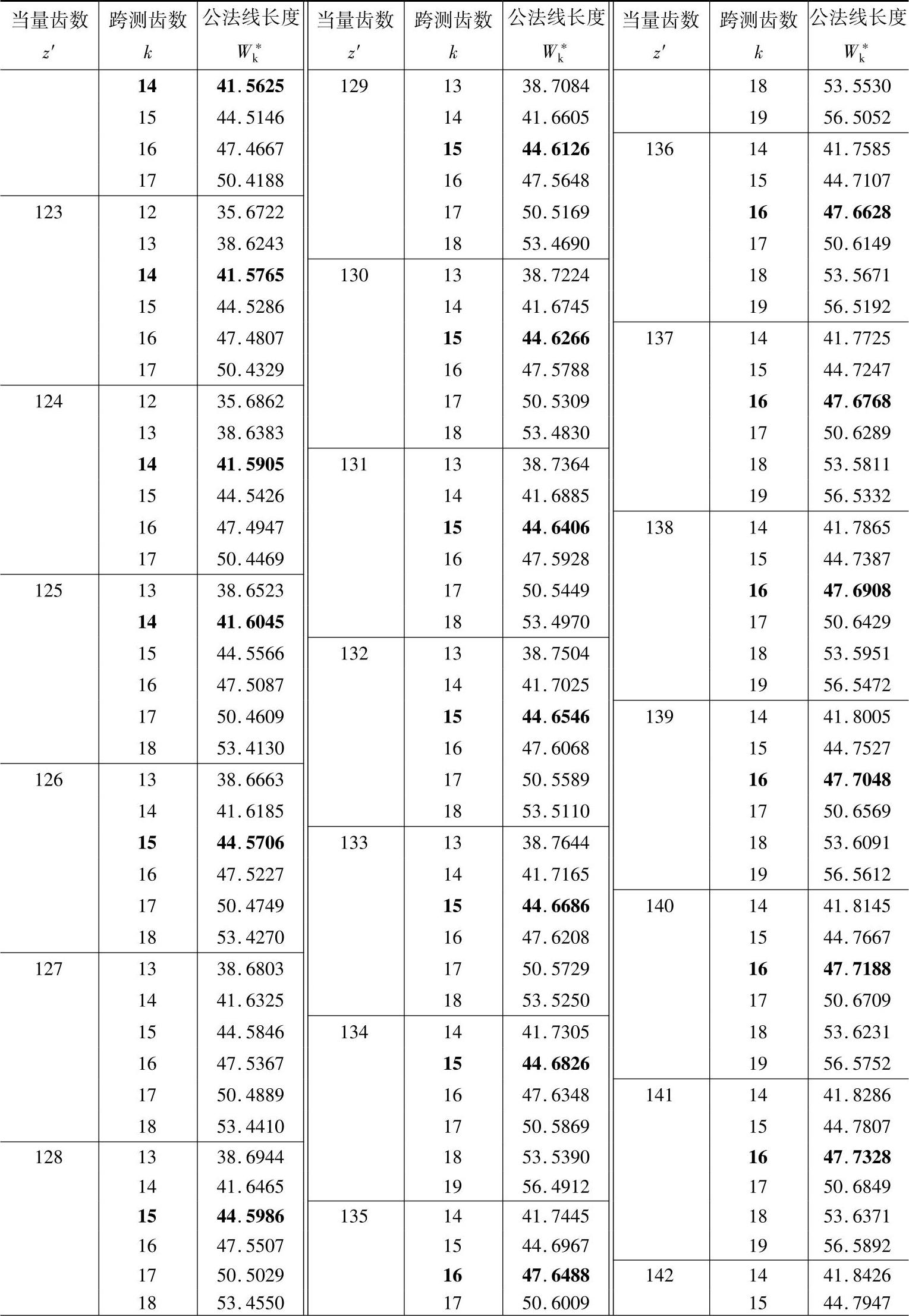
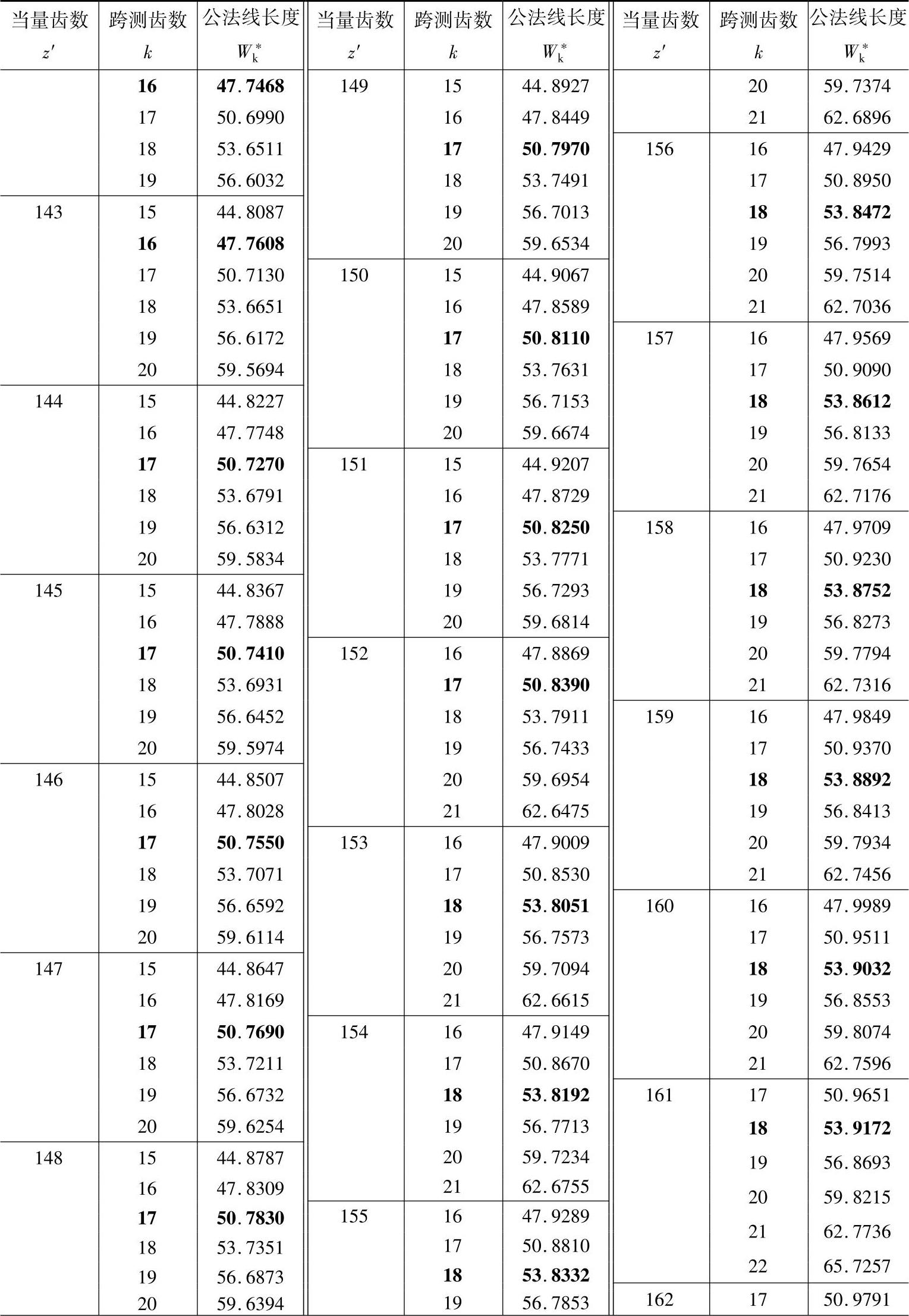
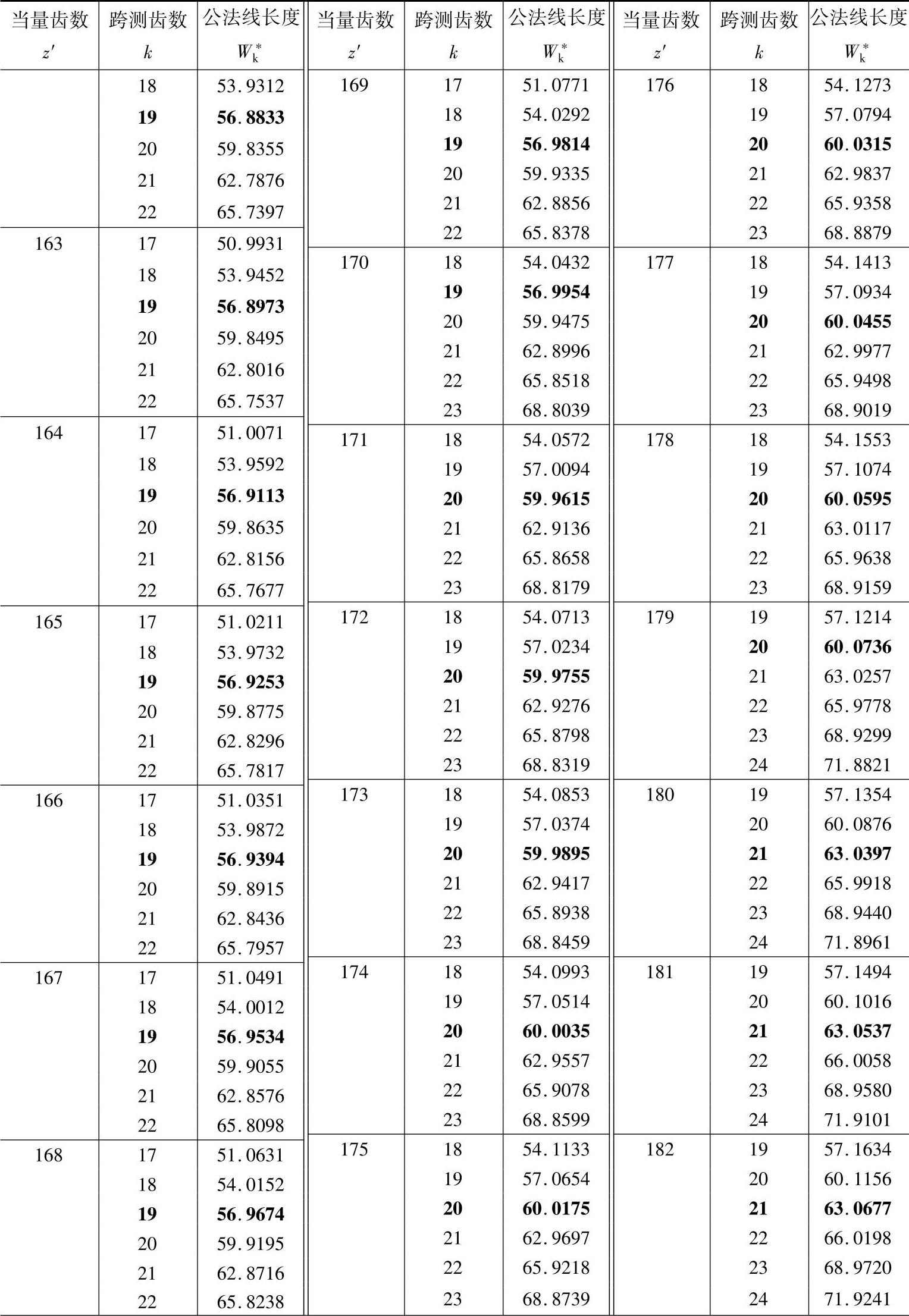
表11-3 公法线长度（m=m_n=1，α=α_n=20°） （单位：mm）

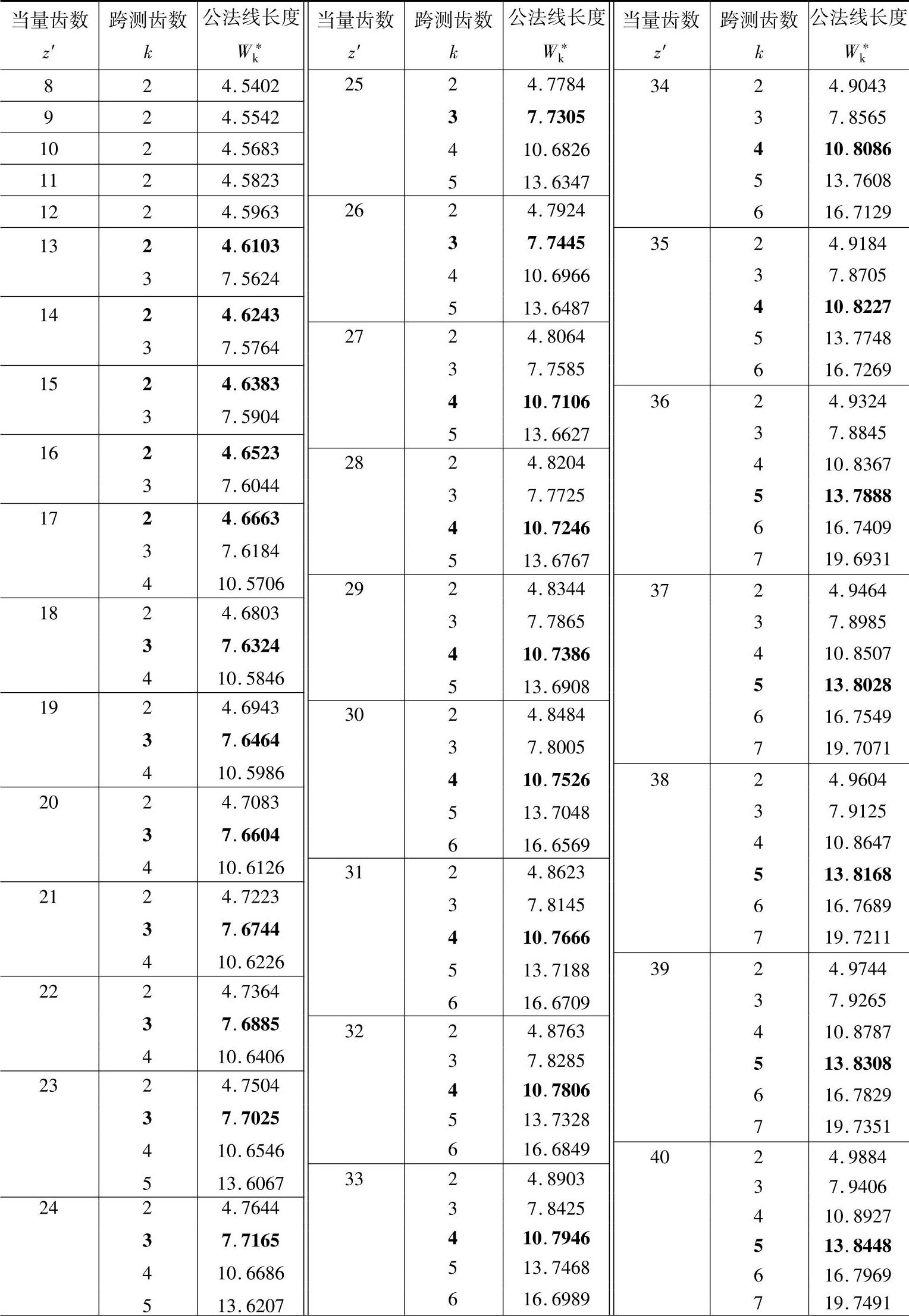
（续）

（续）

（续）

（续）

（续）

（续）

（续）

（续）

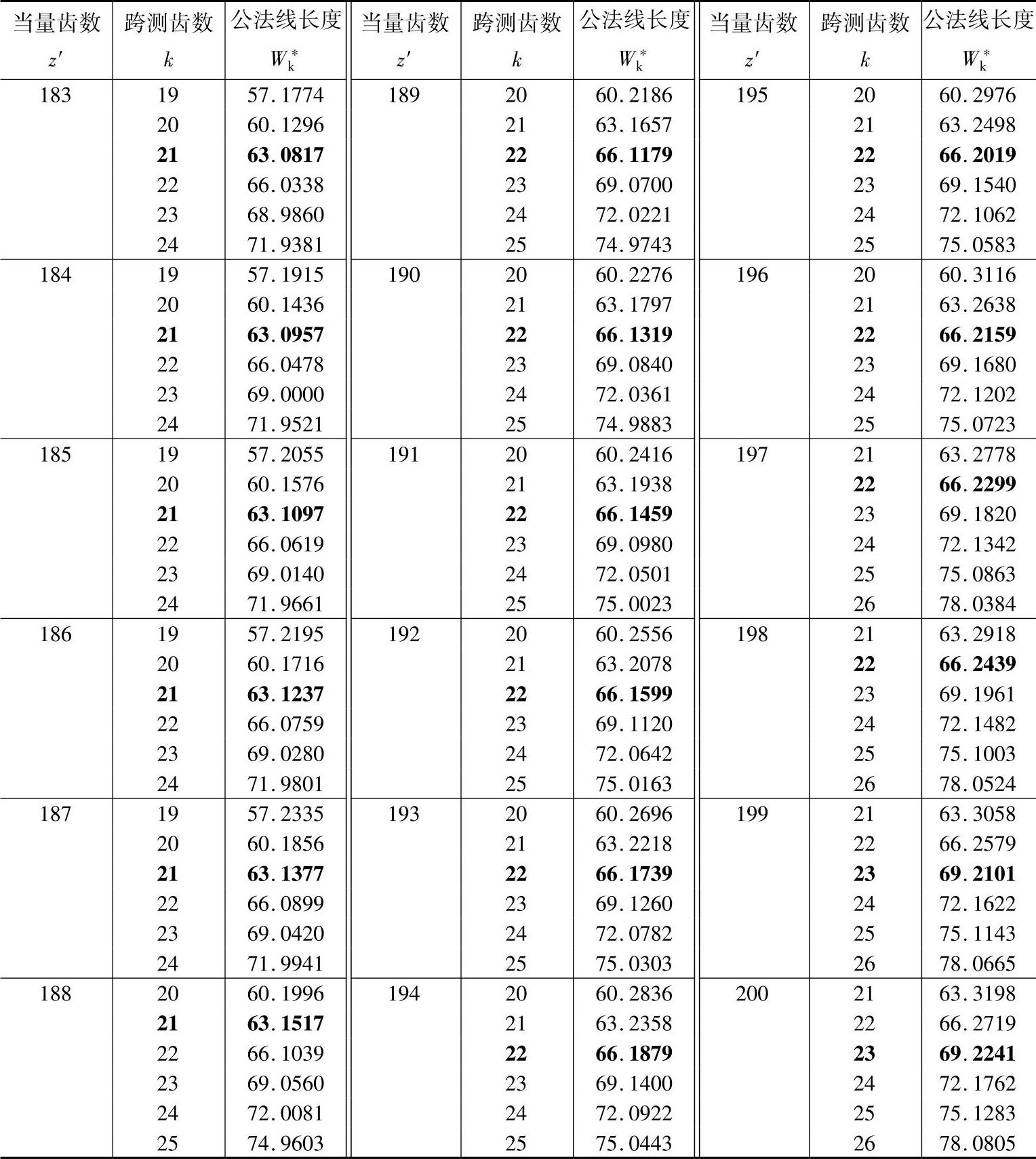
注：1.本表可用于外啮合和内啮合的直齿轮和斜齿轮。对直齿轮z′=z，对斜齿轮。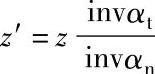

2.对内齿轮k为跨测齿槽数。黑体字是标准齿轮（x=x_n=0）的跨测齿数k和公法线长度W^*_k。

3.对于标准直齿轮，跨测齿数k和m=1时W^*_k查表中的黑体字，然后乘以模数m，使得实际的

公法线长度。所谓公法线长度就是基圆的切线与两侧异名齿廓在分度圆上交点间的实际长度，

所以黑体字是测量标准齿轮公法线的最佳位置值。

对于变位直齿轮，α=20°时的公法长度，W_k=（W^*_k+ΔW_k）m=（W^*_k+2xsinα）m=

（W^*_k+0.684x）m，其中x—变位系数，计及正负号。跨测齿数由计算确定，当x≤0.3时，K

按黑体字查用，影响不大。

4.内齿轮公法线长度计算公式与外齿轮一样，其差别是外齿轮的k为跨测齿数，内齿轮的k为跨

测齿槽数。外齿轮的上下极限偏差为负值，而内齿轮均为正值，大值为上极限偏差。

表11-4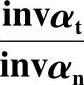值（α_n=20°）

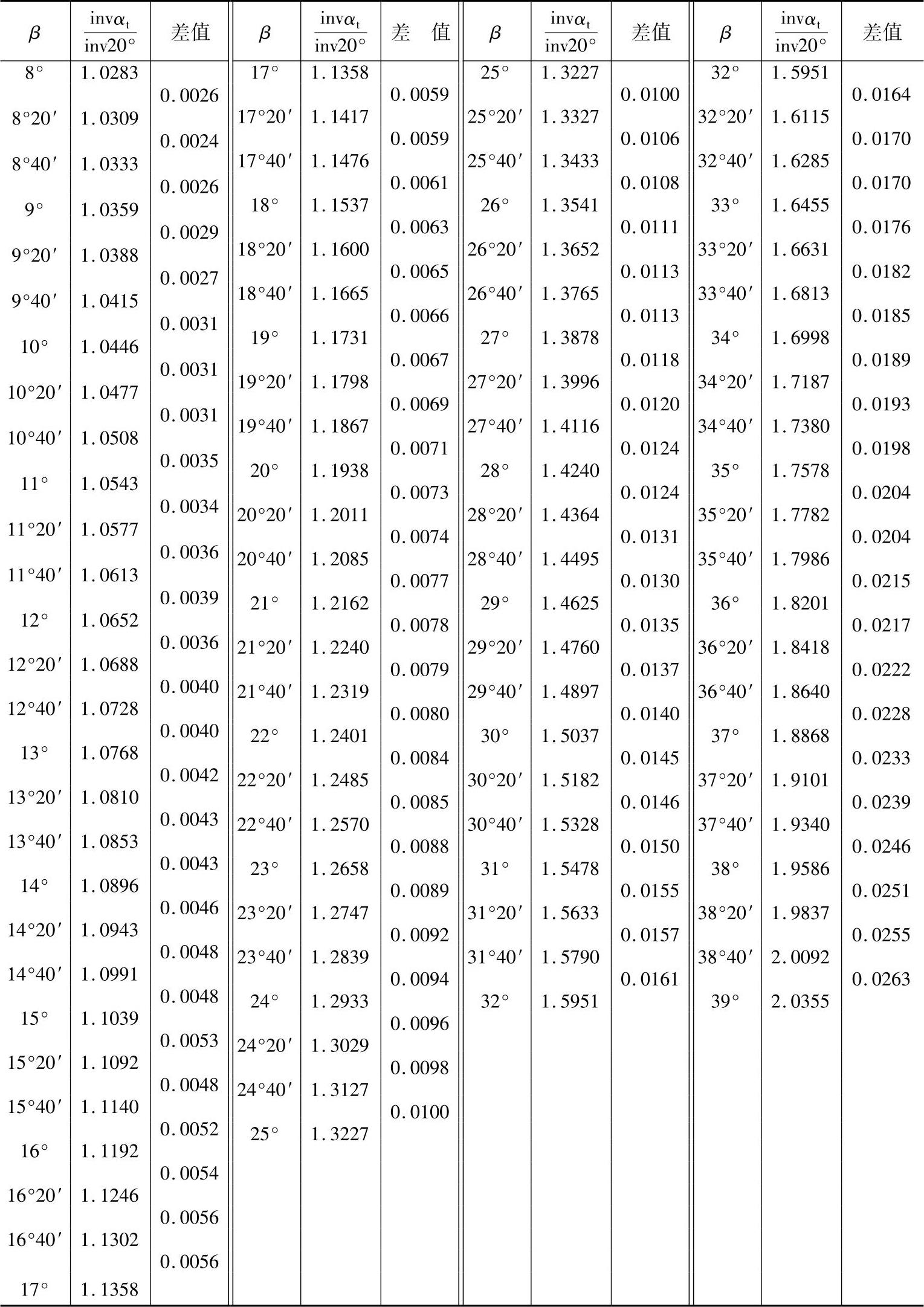
表11-5 当量齿数的小数部分的公法线长度W^*_k（m_n=1，α_n=20°）

表11-6 变位齿轮的公法线长度附加量ΔW^*（m=m_n=1，α=α_n=20°）

（续）

3.斜齿圆柱齿轮公法线长度的简易计算

斜齿轮公法线长度是在法向测量的，因此需要计算法向的公法线长度。斜齿轮端面上的形状和尺寸计算关系与直齿轮是相同的，而参数和尺寸都应是端面的，所以斜齿轮端面公法线长度W_kt的计算公式和直齿轮相似。将端面参数代入直齿轮公式，可得出：(www.xing528.com)

W_kt=m_tcosα_t[（k-0.5）π+zinvα_t]

式中 m_t——端面模数，m_t=m_n/cosβ；

α_t——端面压力角，tanα_t=tanα_n/cosβ。

斜齿轮法向公法线长度W_kn与端面公法线长度W_kt的关系，可从基圆柱展开图（见图11-1）中看出：

W_kn=W_ktcosβ_b

式中 β_b——斜齿轮基圆柱螺旋角。

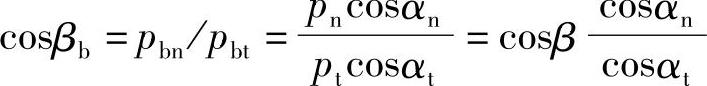
式中 p_bn——法向基节，p_bn=p_ncosα_n；

p_bt——端面基节，p_bt=p_tcosα_t；

p_n——法向齿距；

p_t——端面齿距；

β——斜齿轮分度圆柱螺旋角。

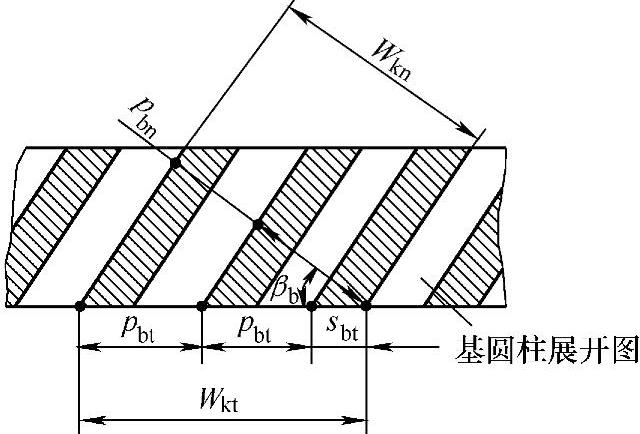
图11-1 斜齿轮公法线长度Wkn

斜齿圆柱齿轮公法线长度简化计算，并计及变位系数的影响，将上式化简，得

W_kn=m_ncosα_n[（k-0.5）π+zinvα_t+2x_ntanα_n]=m_n[K₁+zK₂+2x_nsinα_n]

式中 K₁——计算系数，见表11-7，K₁=π（k-0.5）cosα_n；

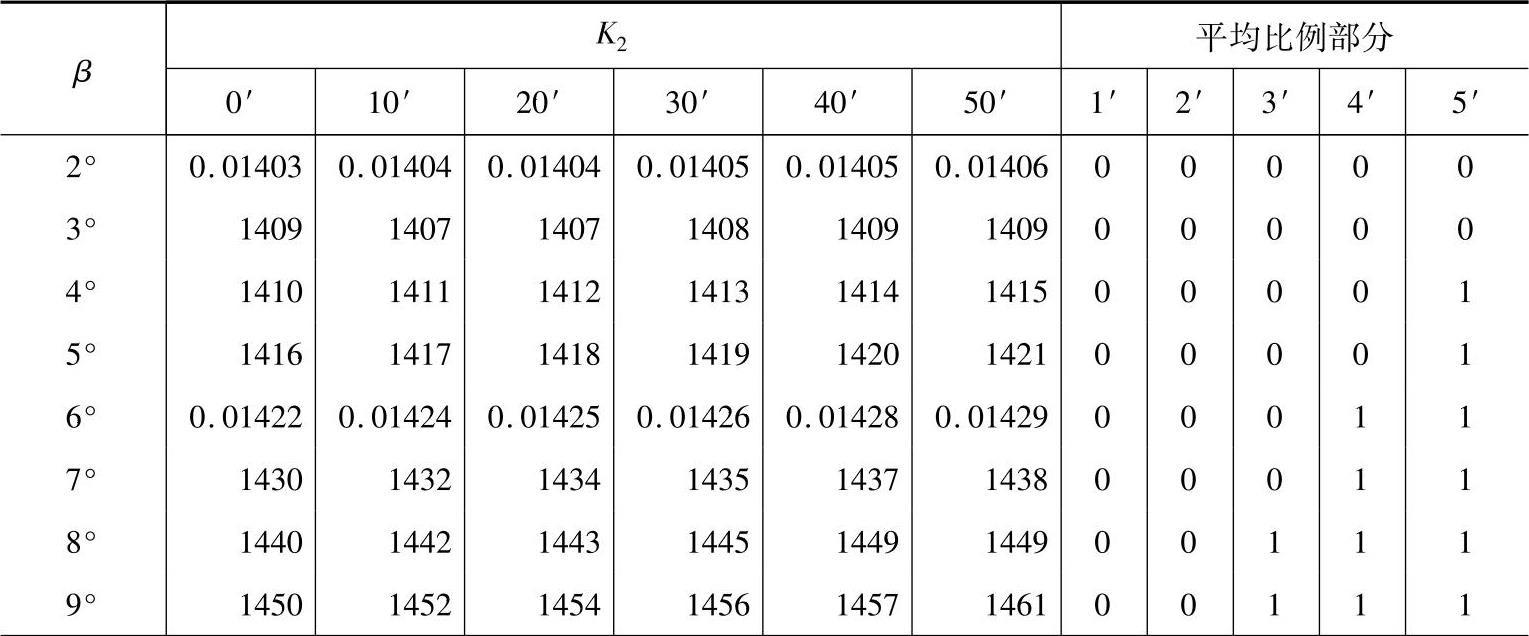
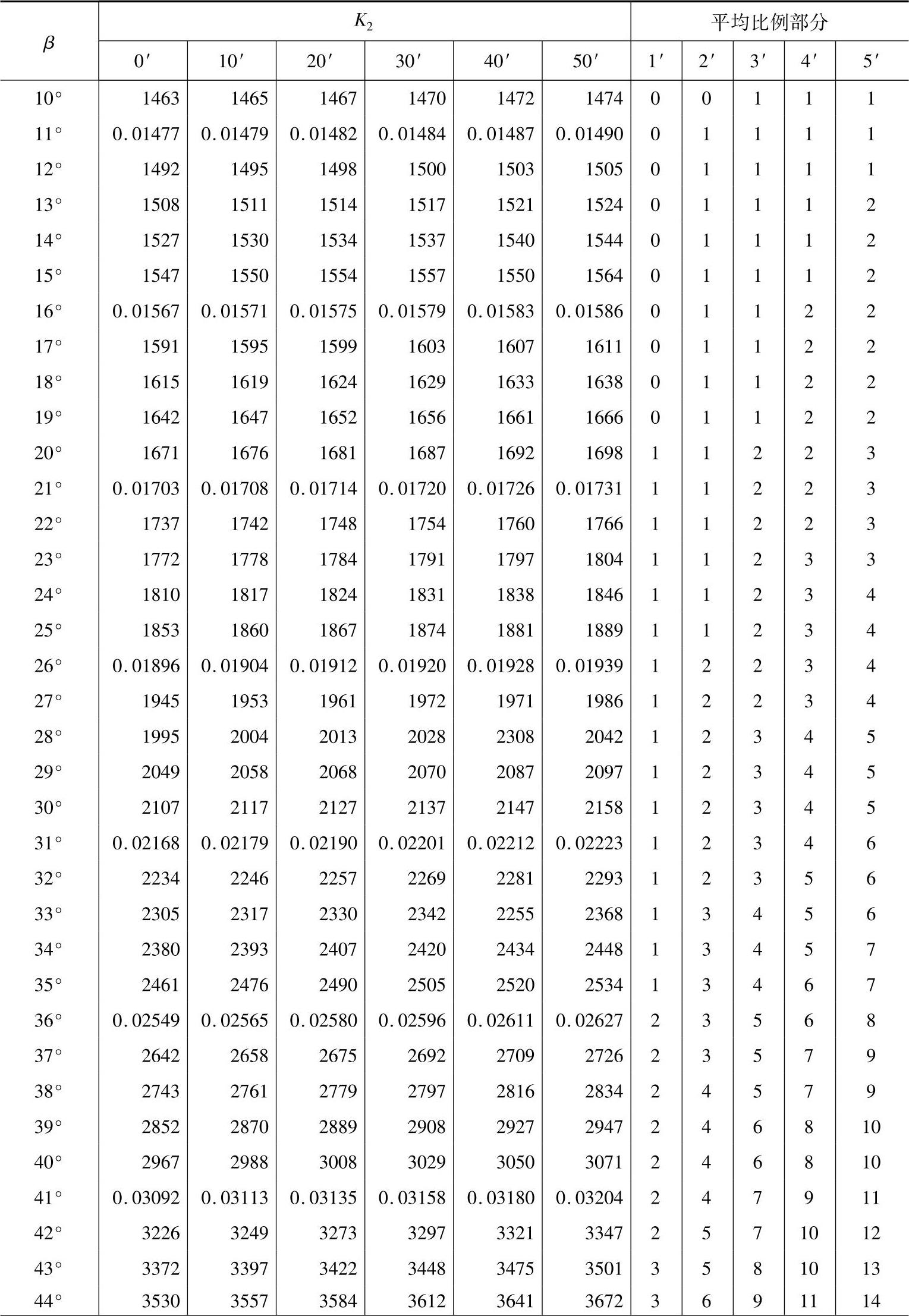
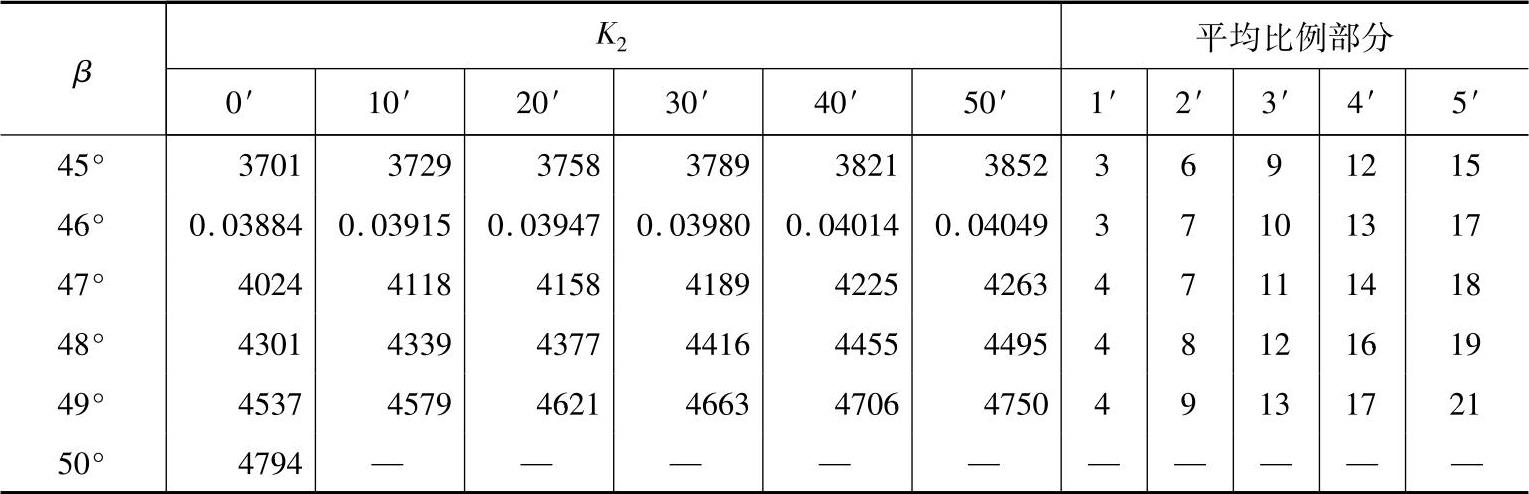
K₂——计算系数，见表11-8，K₂=invα_tcosα_n。

当α_n=20°时，2x_nsinα_n=2x_nsin20°=0.684x_n。

表11-7 K₁值

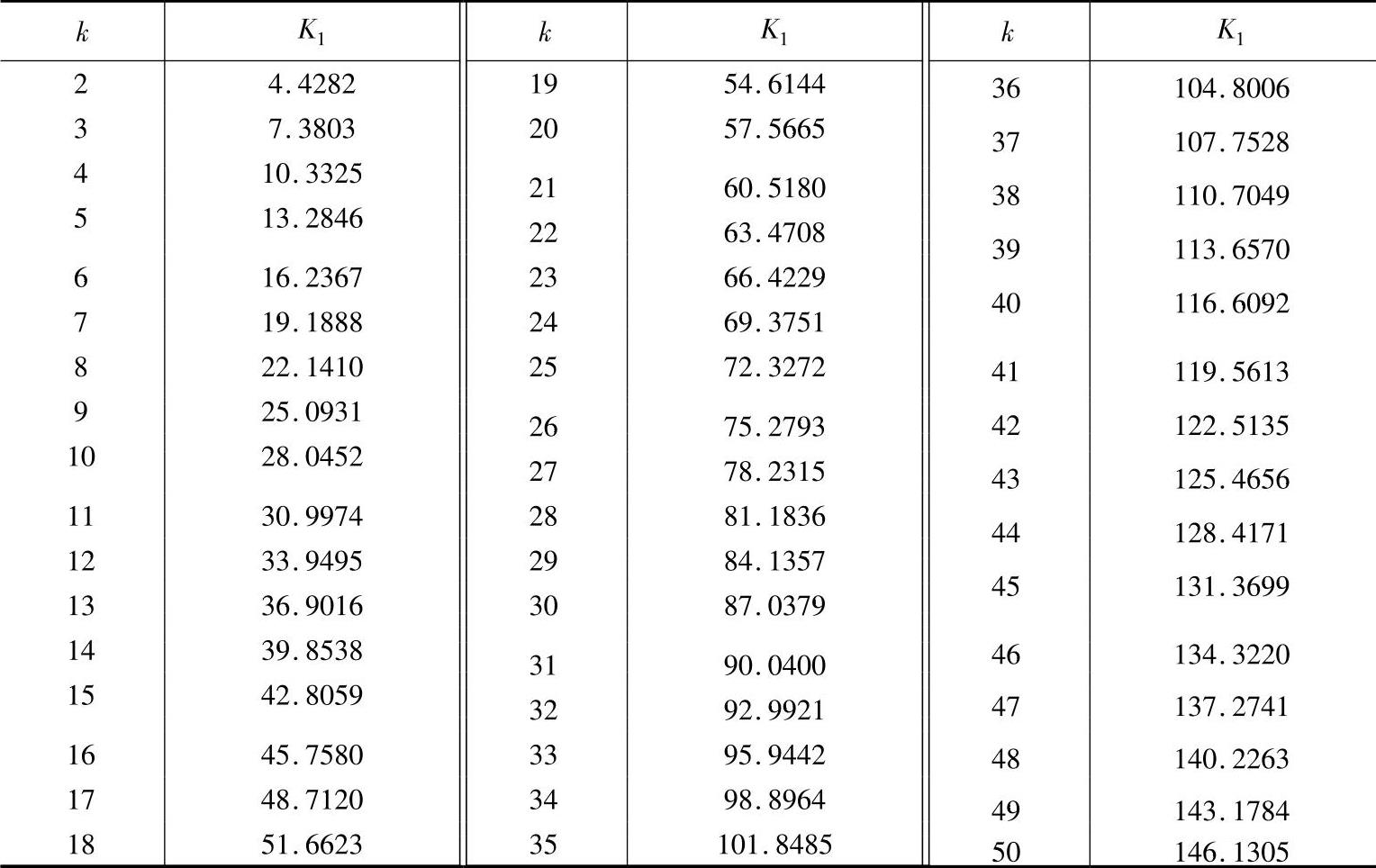
表11-8 K₂值

（续）

（续）

【例11-2】已知一斜齿圆柱齿轮的法向模数m_n=4mm，压力角α_n=20°，齿数z=74，变位系数x_n=-0.2，分度圆螺旋角β=21°8′，试确定公法线长度W_kn。

解 1.计算法

W_kn=m_ncosα_n[（k-0.5）π+zinvα_t+2x_ntanα_n]

1）cosα_n=cos20°=0.93969

2）k=0.111z′+0.5

因z′=z/cos³β=74/cos³21°8′=74/（0.93274）³=91.19

取z′=91，则

k=0.111×91+0.5=10.6

取k=11

3）invαt

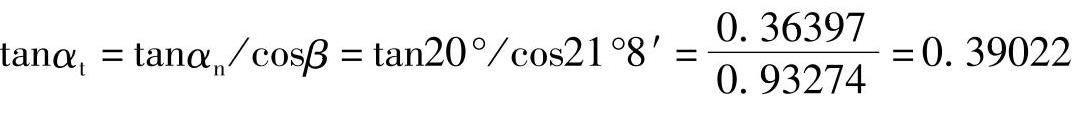
查渐开线函数表α_t=21°19′，得

invα_t=inv21°19′=21°19′=0.01817

4）代入公式

W_kn=4mm×0.93969[（11-0.5）×3.1416+74×0.01817-0.684×0.2]=128.493mm

2.简化算法

查线图11-2得k=11，由表11-7，得K₁=30.9974。

根据β=21°8′，由表11-8，得K₂=0.017076，则

W_kn=m_n（K₁+zK₂+2x_nsinα_n）=4（30.9974+74×0.017076-0.684×0.2）mm=128.497mm

两种算法得到结果相差无几，但用简化算法计算简便，不易出差错。

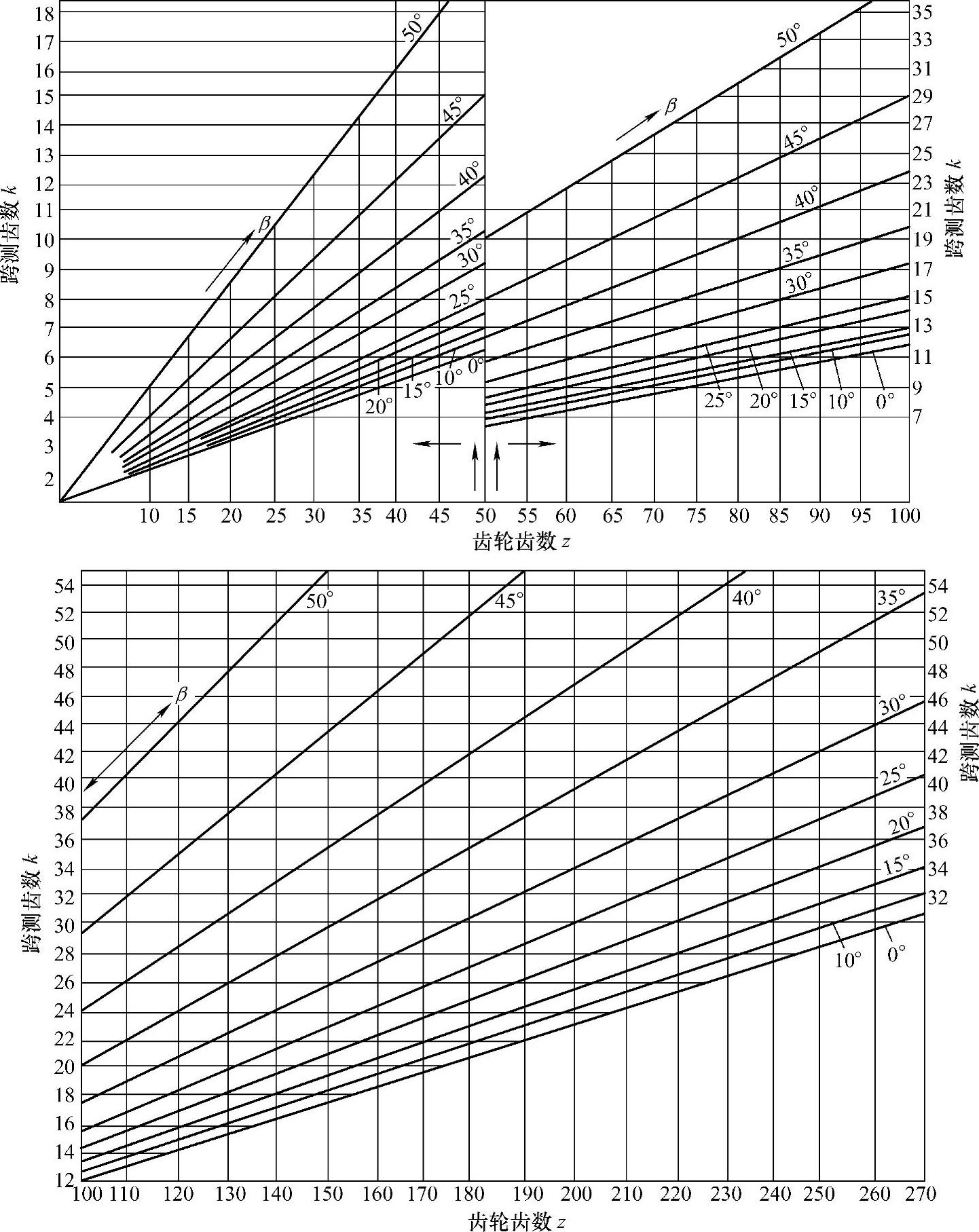
图11-2 跨测齿数k的确定