斜齿轮传动的特点与应用

1）一对斜齿轮相啮合时，以一个齿轮齿顶上的一点与另一齿轮的齿根相啮合，然后接触线逐渐增大，又逐渐缩至一点，如图7-13所示，最后脱离啮合。与直齿轮相比，其冲击和噪声都较小，传动较平稳。

2）斜齿轮的接触线是斜的，又由于重合度较大，斜齿轮的接触线总长度较大，故齿面的单位压力较小，因此，斜齿轮的承载能力比直齿轮有所提高。

3）斜齿轮不产生根切的最少齿数比直齿轮的少。

4）由于斜齿轮的轮齿是斜的，位于同一圆柱面的齿廓上的各点不同时参与啮合，这样可以分散制造误差对传动的影响。

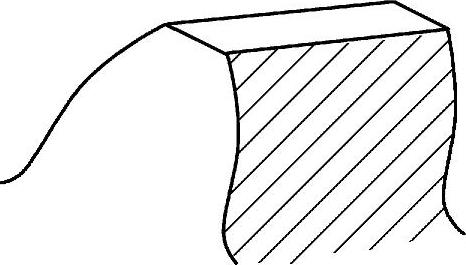
图7-13 斜齿轮的接触线

5）由于斜齿轮的轮齿是斜的，将产生轴向力，且增加了摩擦损失，降低了传动效率。

【例7-1】试设计一对斜齿轮，设z₁=8，z₂=50，m_n=2，α_n=20°，h^*_an=1，c^*_n=0.25，齿宽b=20mm。为避免根切，取较大的螺旋角β₁=-β₂=30°。

解（1）求端面参数 端面模数m_t=m_n/cosβ=2mm/cos30°=2.3094mm

端面分度圆压力角α_t=atctan（tanα_n/cosβ）=arctan（tan20°/cos30°）=22.79588°

端面齿顶高系数和顶隙系数

h^*_at=h^*_ancosβ=1×cos30°=0.8660254

c^*_t=c^*_ncosβ=0.25×cos30°=0.2165064

标准斜齿轮避免根切的最少齿数

z_min=2h^*_at/sin²α_t=2×0.8660254/sin²22.79588°=11.538

齿轮1避免根切的最小变位系数xt1min

取x_t1=0.31，x_t2=0。

端面啮合角α_t′

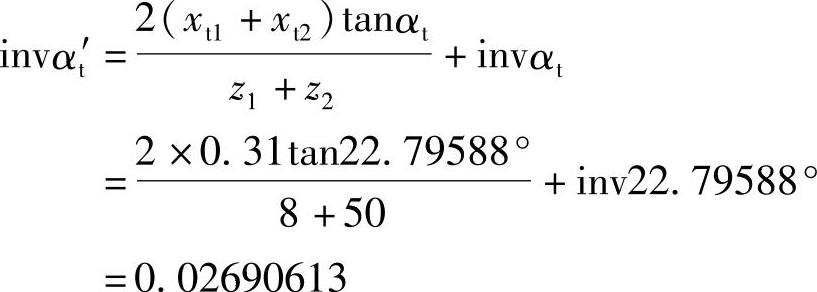
查渐开线函数表得α_t′=24.15963°中心距a′

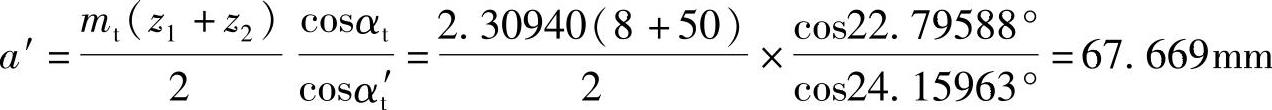
端面中心距变动系数yt

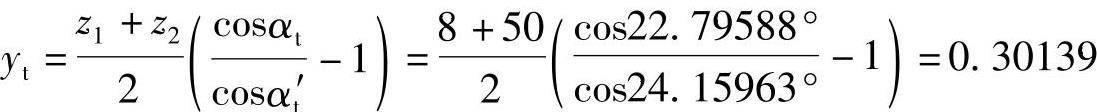(www.xing528.com)

齿顶高变动系数Δy_t

Δy_t=xΣt-y_t=x_t1+x_t2-y_t=0.31-0.30139=0.00861

两齿轮的分度圆直径

d₁=m_tz₁=2.3094×8mm=18.475mm

d₂=m_tz₂=2.3094×50mm=115.470mm

两齿轮的顶圆直径

d_a1=m_t（z₁+2h_a*t+2x_t1-2Δy_t）=2.3094（8+2×0.8660254+2×0.31-2×0.00861）mm=23.867mm

d_a2=m_t（z₂+2h_a*t+2x_t2-2Δy_t）=2.3094（50+2×0.8660254+0+2×0.00861）mm=119.43mm

两齿轮的基圆直径

d_b1=d₁cosα_t=18.475cos22.79588°mm=17.032mm

d_b2=d₂cosα_t=115.470cos22.79588°mm=106.450mm

（2）校核小齿轮的齿顶厚 齿轮1的齿顶压力角

齿顶厚大于0.4m_t，故可用。

（3）校验重合度 齿轮2的齿顶压力角

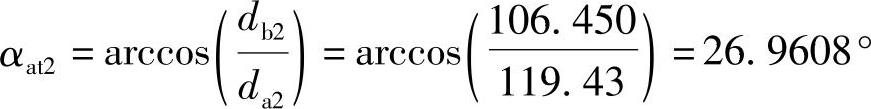
则端面重合度为

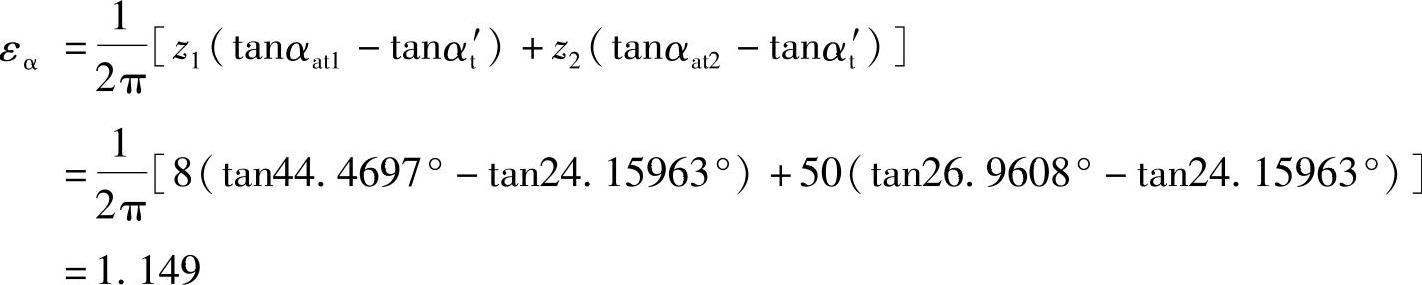
纵向重合度

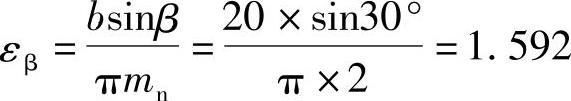
总重合度

ε_γ=ε_α+ε_β=1.149+1.592=2.741

本例也可用法向参数进行计算或用线图法进行计算，更简便。