斜齿轮法向齿廓优化技巧

由斜齿轮齿面的形成原理可知，斜齿轮端面是渐开线齿形。由于斜齿轮的轮齿与轴线呈一螺旋角β，所以斜齿轮的法向齿廓不是渐开线齿形。精确计算法向齿廓是较复杂的，在上节中提到，成形刀具加工斜齿轮时，即使在法向，被加工齿轮的齿形也与刀具的齿形不同，为了在端面得到准确的齿形，需要用精确的方法来计算成形刀具的齿廓。现以指状铣刀为例，说明刀具齿形与被加工斜齿轮法向齿廓间的关系。

用指状铣刀加工齿轮时，如图7-11所示，铣刀的轴线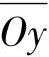和齿轮的轴线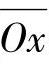相交而且垂直。通过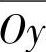轴作平面P—P垂直于齿轮的轴线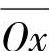，在此平面内，齿间的截面齿形对称于轴线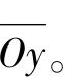

加工时，刀具绕本身轴线Oy旋转，以产生切削运动，同时，齿轮也绕本身轴线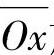旋转并沿轴向移动，两者的配合，便得到螺旋运动。但由于斜齿轮的齿槽为螺旋形，所以铣刀齿形与在剖面P—P中齿轮齿槽的截面齿形是不同的，其与齿槽的法向截面齿形也不相同。当量齿轮的齿槽两侧都是渐开线螺旋面，铣刀的齿形应是：其绕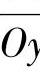y轴旋转而得到回转表面，此表面应与齿槽两渐开线螺旋面相切，如图7-11中的Q—Q截面。作平面Q—Q平行于坐标平面xOz，此Q—Q平面与齿槽两侧渐开线螺旋面相交得到两条对称于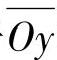轴的曲线aa。Q—Q平面与铣刀齿形的回转表面相截得一圆，此圆应和两曲线aa相切于两对称点M，此圆半径为R₀，Q—Q平面与xOz平面间的距离为y₀，当高度y₀改变时，aa曲线及半径R₀的圆也随之改变，但仍需相加。这样，在各不同高度y₀中的R₀值和相应的y₀就决定了指状铣刀的齿形。在Q—Q剖面中的aa曲线，是已知的渐开线螺旋面和平面Q—Q的交线。

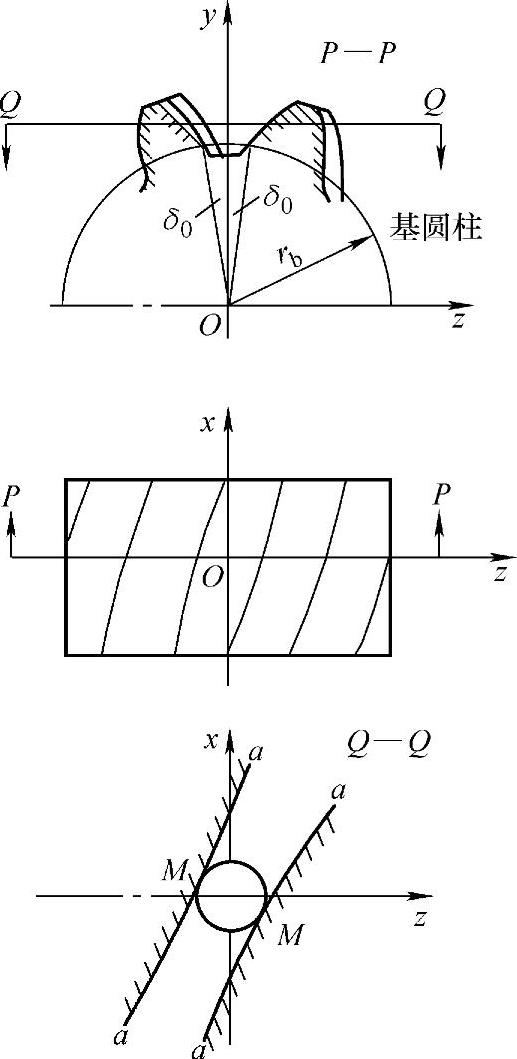
图7-11 铣刀加工斜齿轮的情况

综合上述，为了确定y₀及R₀，用某一y₀值的与铣刀轴线垂直的平面Q—Q截齿廓时，得到在这截面中斜齿轮齿面曲线的方程，用y=y₀=常数，代入渐开线螺旋面的公式，即aa曲线方程。在此截面中铣刀的半径R₀应与aa曲线相切，切点M应同时在aa曲线上，满足aa的方程。经过计算，便可得到指状铣刀齿形上各点的坐标为

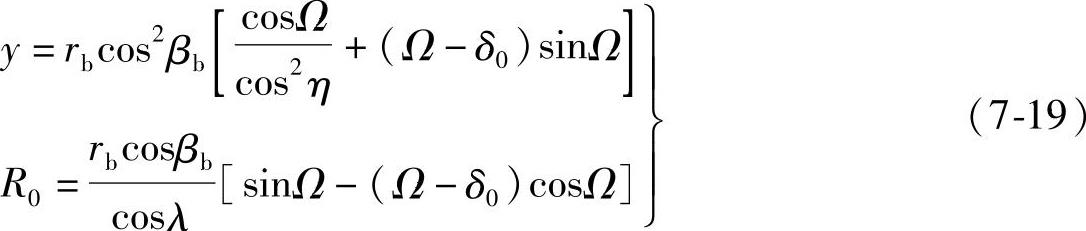
式中 Ω=φ+δ₀

φ——端面渐开线上某点的展开角，φ=θ+α；

δ₀——基圆上半齿槽所对中心角。

为了简化计算，令

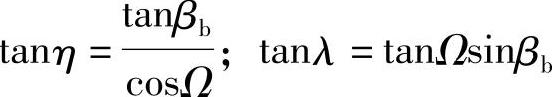
故式（7-19）中的η、λ可由上式求出。

根据式（7-19），给以不同的y值便可求得指状铣刀的精确齿形。(www.xing528.com)

通常，采用近似方法来计算法向齿廓。

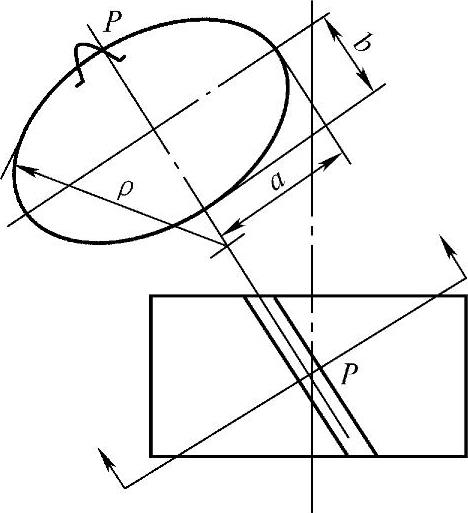
图7-12 斜齿轮近似法向齿廓

如图7-12所示，沿斜齿轮轮齿法线方向将齿切开，得一椭圆形剖面。在此剖面上，节点P附近的齿形可以认为是斜齿轮的法向齿廓，在椭圆其他地方，由于截面不垂直于螺旋线，故切出来的齿形不是法向齿廓。此斜齿轮的法向齿廓不是渐开线，但可近似看作渐开线齿形。其模数m_n、压力角α_n是标准的，椭圆在节点处的曲率半径为ρ，设以此法向齿廓为齿形的齿轮分度圆半径为r_v，且r_v=ρ。这就是说模数为m_n、压力角为α_n、分度圆半径为rv的一个直齿齿轮的齿形与此斜齿轮的法向齿廓是相似的。这个直齿齿轮称为当量齿轮，其齿数称当量齿轮的齿数。根据几何关系可知

式中 b——椭圆短轴，b=r，其中r为斜齿轮分度圆半径，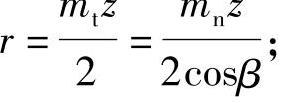

a——椭圆长轴，a=r/cosβ；

r_v——当量齿轮的分度圆半径，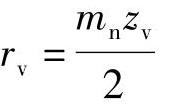

将以上各部分代入式（7-20）后，得

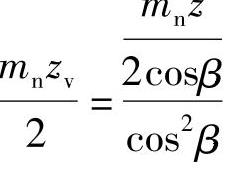
最后得

z_v=z/cos³β （7-21）

齿数z_v为齿数为z的斜齿轮的当量齿数。其意义为，以斜齿轮法向参数m_n、α_n和当量齿数z_v为参数的直齿圆柱齿轮的齿形，与该斜齿轮的法向齿廓是相似的。利用此当量齿数可在计算齿轮强度时求其法向齿廓；另外用成形法加工斜齿轮时，用标准盘形铣刀或指状齿轮铣刀，铣刀刀号数应按式（7-21）算出的当量齿数来选。