斜齿轮传动的几何计算方法优化

由斜齿轮齿面的形成可知，斜齿轮在端面上具有渐开线齿形，但由于斜齿轮的轮齿是螺旋形的，故在垂直于轮齿螺旋线方向，即法平面上，其齿形与端面上是不同的。

斜齿轮加工也有成形法和展成法两种。成形法加工时，使用的刀具有盘形铣刀、指状铣刀及成形齿轮切割刀盘等。用成形法加工斜齿轮时，铣刀装在齿的法向。由于刀具和齿轮有相对的螺旋走刀运动，即刀具与齿轮实际上是处于展成运动之中，故切削出齿轮，即使在法向截面中，也与刀具的齿形不同，在端面中其齿形相差更大，故成形法只能用于加工精度较低的斜齿轮。若要制造精确的斜齿轮可用展成法，展成法使用的刀具有插齿刀和滚刀。加工斜齿轮的插齿刀是斜齿的，加工时刀具要实现螺旋，插齿机要有带螺旋槽的滑枕，从而使插齿机复杂化，同时降低加工精度。近年来，由于数控插齿机的出现，可不用滑枕即能加工任意螺旋角β的斜齿轮。通常β≤30°，为了便于在数控磨齿机上磨内斜齿轮，一般要求β≤25°。

用滚刀加工齿轮的原理，相当于一对交错轴斜齿轮的啮合原理（旧称螺旋齿轮）。一对正确啮合的交错轴斜齿轮，其轮齿必须能与一个空间齿条（原始齿廓）正确啮合。为此，这两个齿轮在同一齿条的法向截面n—n中必须有相同的齿距和压力角（见图7-6）：用滚刀加工齿轮时，也应该满足这个条件，将滚刀看成一个齿数很少的斜齿轮，即被加工齿轮在法向截面应具有和刀具相同参数，如模数、压力角等，这些参数都是标准值。但斜齿轮的端面是渐开线的，其几何尺寸的计算按照端面参数进行计算，所以应进行法向参数与端面参数的换算，即将法向参数m_n、α_n、h^*_an、c^*_n换算成端面参数m_t、α_t、h^*_at、c^*_t。

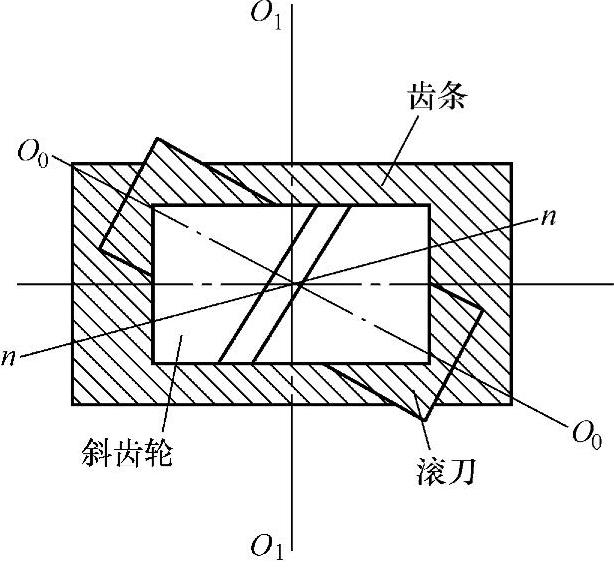
图7-6 斜齿轮加工原理

通常法向参数为标准参数，m_n、α_n、h^*_an、c^*_n，斜齿轮分度圆螺旋角β，p_n为斜齿轮分度圆法向齿距，p_t为端面齿距。由图7-6可知

p_n=p_tcosβ （7-8）

而p_n=πm_n，p_t=πm_t，代入上式后可得

m_n=m_tcosβ或m_t=m_n/cosβ （7-9）

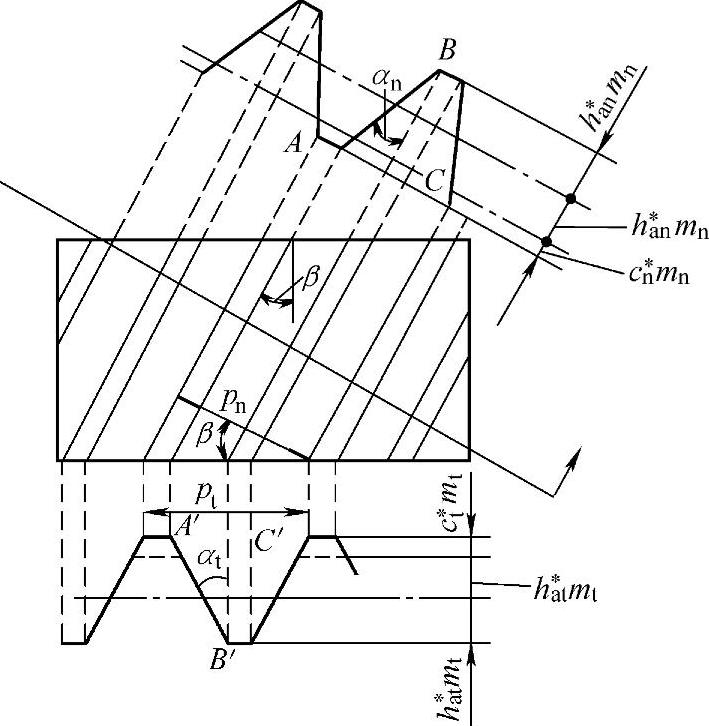
图7-7 斜齿轮的端面法向参数

齿轮轮齿的高度不论在法向或端面，都是相等的，即

h^*_anm_n=h^*_atm_t

c^*_nm_n=c^*_tm_t

由此可得h^*_ancosβ=h^*_at （7-10）

c^*_ncosβ=c^*_t （7-11）

由图7-7可求出法向压力角与端面压力角的换算关系为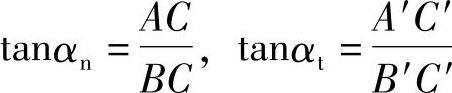

因为齿高是相等的，则BC=B′C′，而

AC/A′C′=cosβ

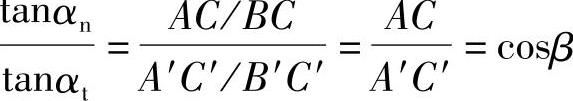
则

因而端面参数与法向参数间的换算关系为

m_t=m_n/cosβ

tanα_t=tanα_n/cosβ

h^*_at=h^*_ancosβ

c^*_t=c^*_ncosβ

斜齿轮不产生根切现象的最少齿数可根据直齿轮的最少齿数公式而得，即

式中 h^*_at、α_t——端面齿顶高系数及端面压力角。

一对α=20°、h^*_a=1的直齿轮不产生根切的最少齿数z_min=17；而一对α=20°、h^*_an=1、β=30°的斜齿轮，其不产生根切的最少齿数为

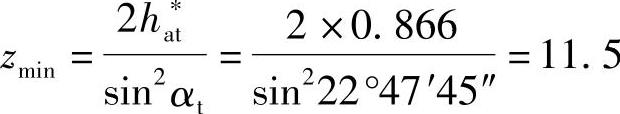
由此可知，标准斜齿轮的最少齿数比直齿轮的少，如增大螺旋角，可使斜齿轮的最少齿数更加减少而不产生根切现象。

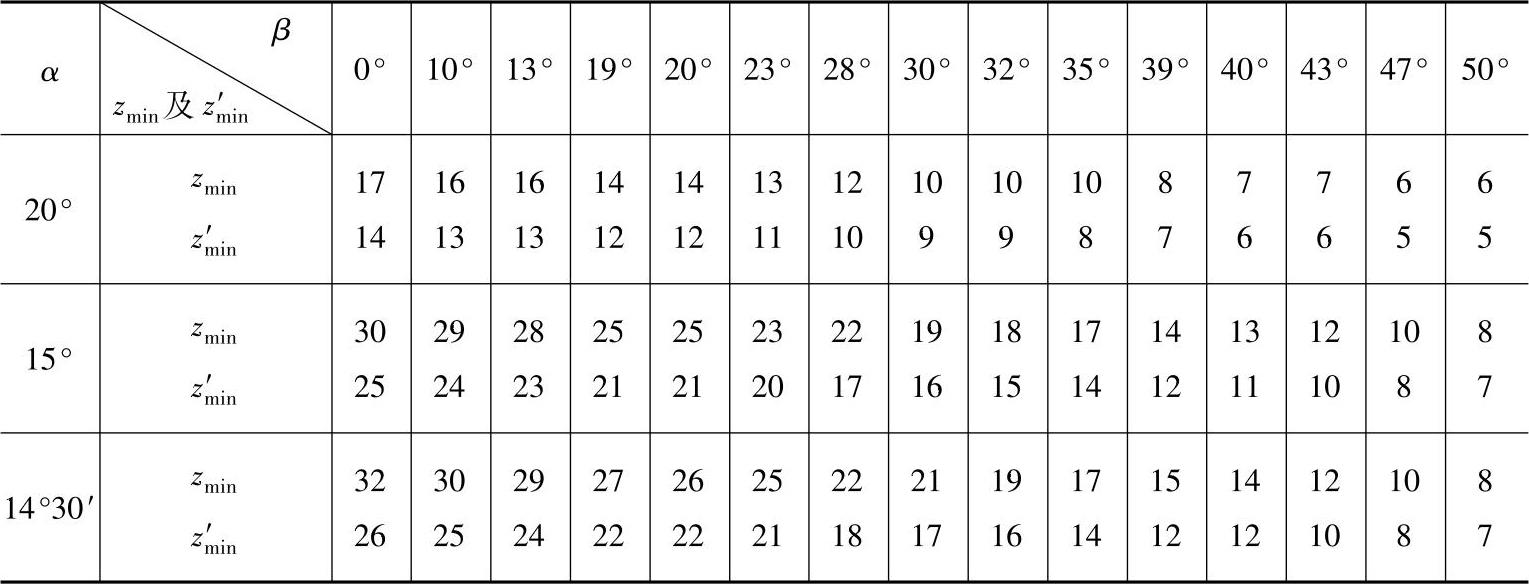
斜齿轮不产生根切和产生微量根切的最少齿数z_min及z_m′_in如表7-1所列。

表7-1 斜齿轮的最少齿数z_min及z_m′_in（h^*_an=1）

一对斜齿轮传动是在两个相互平行轴之间进行的，因此一对斜齿轮传动的正确啮合条件是：两齿轮法向的基圆齿距相等p_bn1=p_bn2，两齿轮的分度圆螺旋角大小相等而方向相反；对于内啮合传动，则分度圆螺旋角大小相等、方向相同。

斜齿轮也可进行变位，其法向变位系数x_n，端面变位系数x_t，由于变位距离不论在法向或端面都是相等的，因此有

x_nm_n=x_tm_t

由此可得端面、法向变位系数的关系为

x_t=x_ncosβ （7-14）

一对斜齿轮传动，也可采用高度变位及角度变位。若采用角度变位中正传动时，啮合角增大，有利于增大轮齿的曲率半径及齿根厚度，但其重合度减小，又使承载能力降低，因而采用变位不一定会带来好处。另外在配凑中心距的问题上，因斜齿轮传动可用改变螺旋角的办法来改变中心距，因此不一定要用变位齿轮。所以斜齿轮传动一般常用标准齿轮传动，有时为了使两齿轮等弯曲强度，或减小滑动率，也可以采用高度变位。

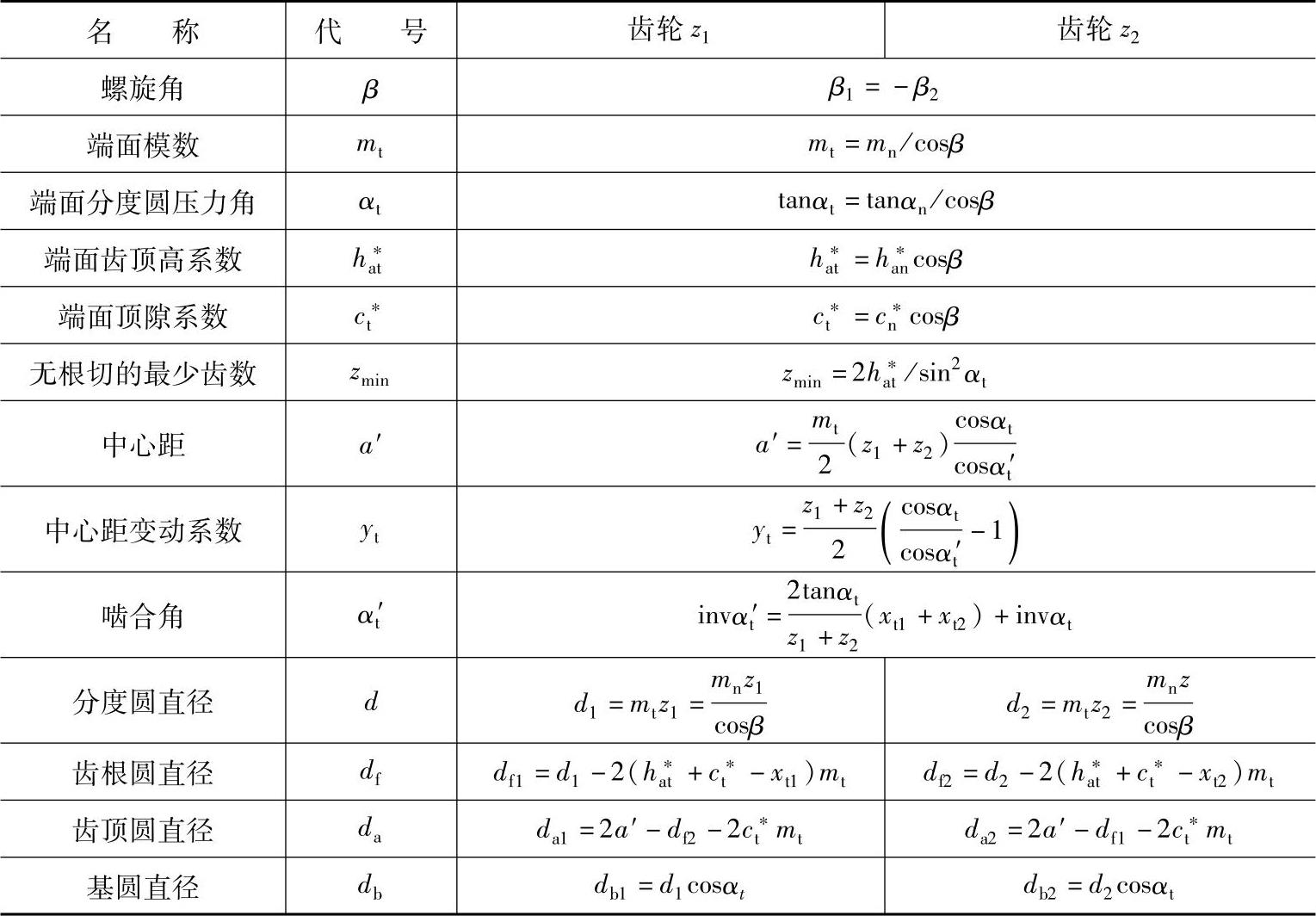
1）斜齿轮传动的几何计算公式，如表7-2所列。(www.xing528.com)

表7-2 斜齿轮传动的几何计算公式

2）斜齿轮的公法线长度计算。作斜齿轮基圆柱的切平面，如图7-8所示。按斜齿轮的形成原理可知，该平面与斜齿轮的两异侧齿面的交线为两条平行的斜直线，同时，它又是斜齿轮齿面的法平面。

斜齿轮的公法线长度W_kn就是这两条平行线间的最短距离。在基圆柱切平面中，齿廓1、2的两端面齿廓间的距离就是端面公法线长度W_kt。端面公法线长度计算公式可借用直齿轮的公式，只需将参数改为端面参数便可。

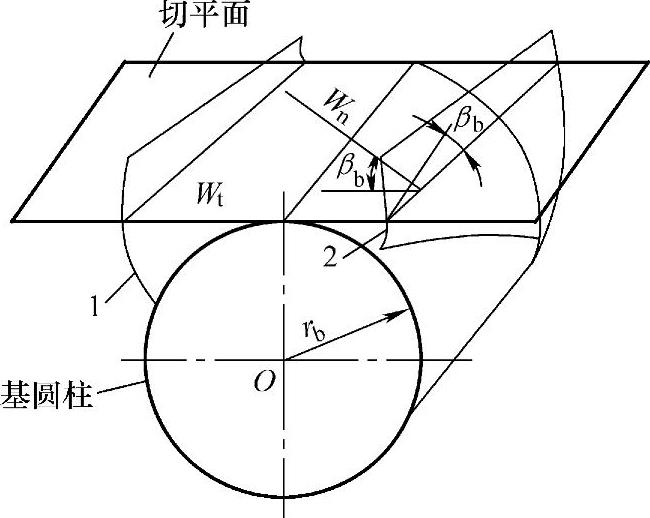
图7-8 斜齿轮的公法线

W_kt=m_tcosα_t[（k-0.5）π+zinvα_t]+2x_tm_tsinα_t （7-15）

式中 z——斜齿轮齿数；

W_k——跨K齿时的端面公法线长度。

由于W_kn=W_ktcosβ_b （7-16）

而

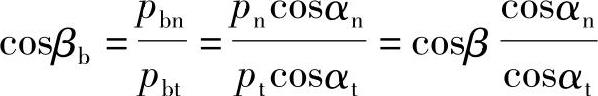
将式（7-15）及cosβ_b代入式（7-16），可得斜齿轮公法线长度为

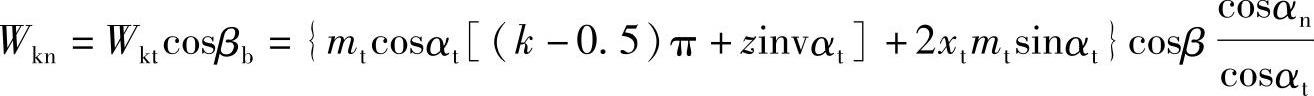
经整理得

W_kn=m_ncosα_n[（k-0.5）π+zinvα_t]+2x_nm_nsinα_n

上式可写成

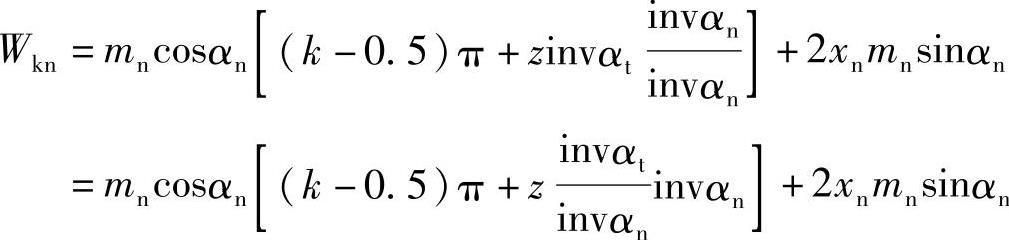
令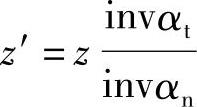，z′称为假想齿数，代入上式得斜齿轮公法线长度计算公式为

W_kn=m_ncosα_n[（k-0.5）π+z′invα_n]+2x_nm_nsinα_n （7-17）

测量斜齿轮公法线长度时，跨测齿数k的计算公式与直齿轮公式相同，只是式中的齿数应以假想齿数z′代入。

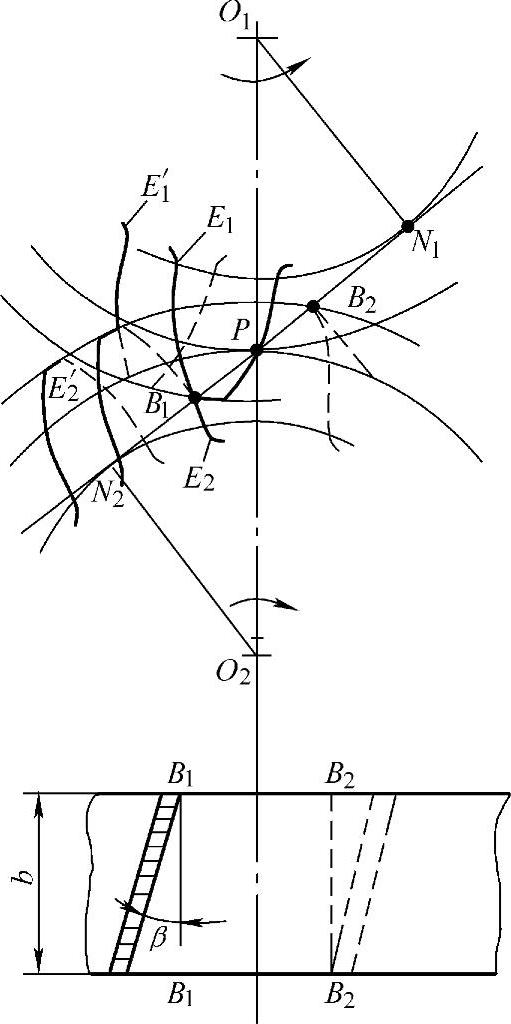
图7-9 斜齿轮的重合度

3）斜齿轮的重合度计算。斜齿轮的螺旋角β，齿宽为b。图7-9中所示，设直线B₁B₁、B₂B₂分别表示在啮合平面内，轮齿进入啮合与脱离啮合时的位置。当斜齿轮的前端面齿廓E₁、E₂进入啮合到达B₁点和脱离啮合到达B₂点时，其啮合情况与一对直齿轮完全相同，但由于斜齿轮轮齿是斜的，所以整个齿宽不是同时全部进入啮合的，而是先由轮齿的一个端面进入啮合，随着轮齿的转动，沿齿宽方向逐渐进入啮合，直到全部齿宽都进入啮合，即E₁′、E₂′到达B₁点。脱离啮合时的情况也与此相似，当轮齿的第一个端面齿廓E₁、E₂到达B₂点时，开始脱离啮合，但这时沿齿宽的其他部分仍在啮合中，直到沿齿宽的最后一个端面，即齿廓E₁′、E₂′到达B₂点时，这个轮齿才算全部退出啮合。由此可知，斜齿轮的实际啮合区比直齿轮的增大了。由图7-9可知，增加了btanβ的距离，故斜齿轮的重合度应为两部分组成，其总重合度为

ε_γ=ε_α+ε_β （7-18）

式中 ε_α——端面重合度，可利用直齿轮的公式

计算，以斜齿轮的端面参数代入；

ε_β——增加部分，称为纵向重合度ε_β。

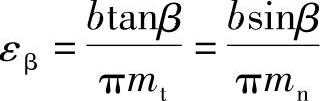
由上式可知，斜齿轮的重合度随斜齿轮分度圆螺旋角β及齿宽b的增大而增加，在理论上螺旋角β和齿宽b都没有限制，所以斜齿轮的重合度可以达到很大的数值，如有些设备中的斜齿轮传动，其重合度ε_γ可达10以上。但随着螺旋角的增大，传动时引起的轴向力也相应增大，通常斜齿轮分度圆的螺旋角取为

斜齿轮传动 β=8°～17°

人字齿轮传动 β=25°～40°

此外，斜齿轮的齿宽b也不能只从增大重合度方面考虑，还应根据制造、安装以及传动的配置、是否悬臂等因素来确定。为了保证有足够的附加重合度，一般使齿宽满足下式

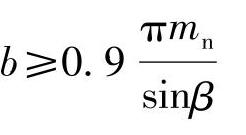
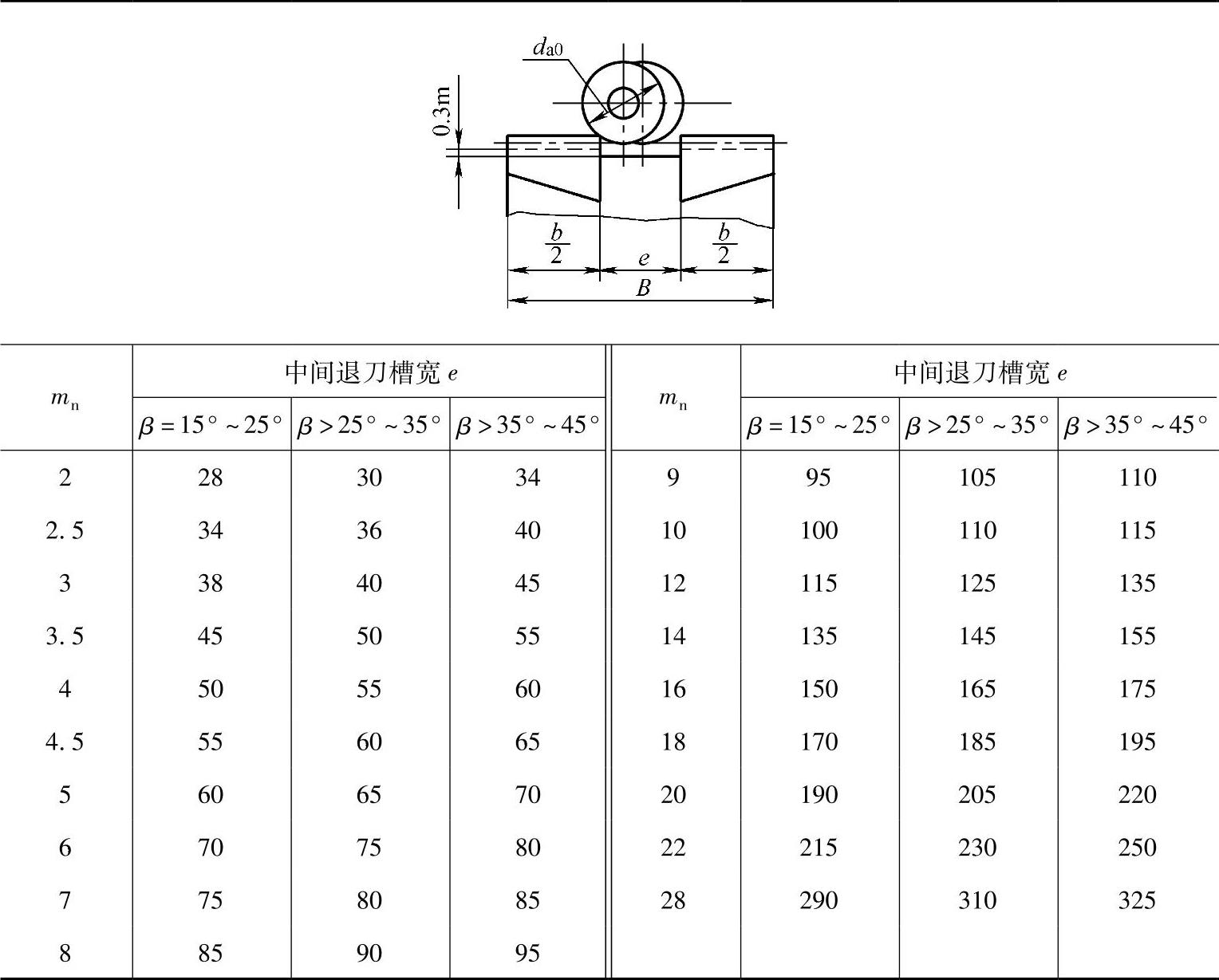
用标准滚刀加工人字齿轮的中间退刀槽的尺寸见表7-3。

表7-3 标准滚刀加工人字齿齿轮的中间退刀槽尺寸 （单位：mm）

4）螺旋方向的确定（见图7-10）。通常，在平行轴两级以上传动的减速器中，螺旋角的旋向影响到轴向力的大小和方向，也影响径向轴承支反力的大小和方向。因此，斜齿轮圆柱齿轮螺旋角的旋向与齿轮轴及箱体的强度、刚度设计、轴承的选择有密切关系，在减速器设计中，是一个极为重要的问题。

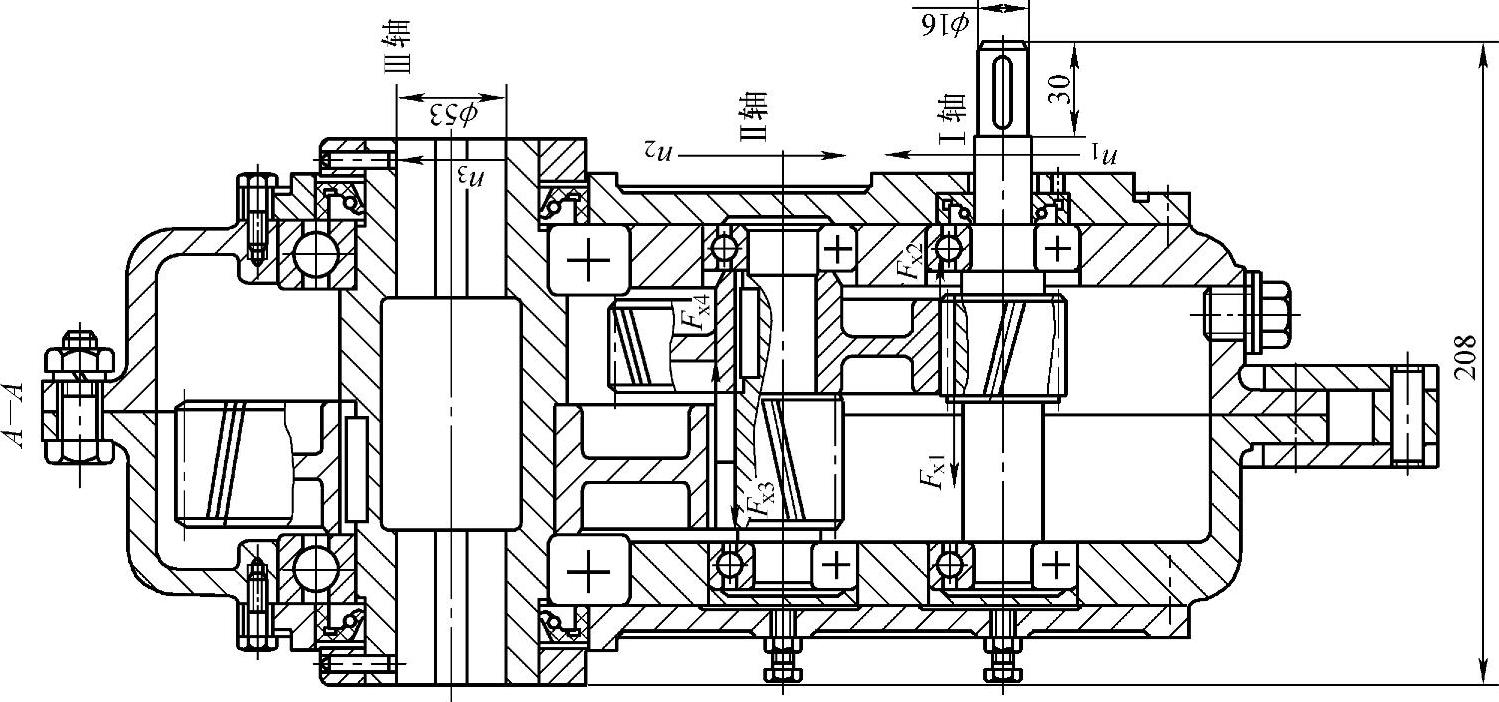
图7-10 斜齿轮减速器轴向力方向的确定

作用在齿轮轴上轴向力的方向可采用“主动轮的左右手定则”来判断。主动轮为右旋时，当紧握右手四指表示主动轮的旋转方向，则与四指垂直的姆指指向就是主动轮上的轴向力方向；主动轮为左旋时，采用左手定则来判断。主动轮轴向力方向确定后，从动轮上的轴向力方向与其大小相等，方向相反。为此，在平行轴传动的减速器设计中，其中间轴上两齿轮旋向相同，使其轴向力相互抵消一部分。在人字齿齿轮传动中，其轴向力相互抵消，可采用较大的螺旋角，为了保证正确啮合，通常将大齿轮固定，而使小人字齿齿轮轴向游动。