斜齿轮的形成原理介绍

1.斜齿轮齿面的形成

设有一平面与基圆柱相切，平面上有一条与基圆柱轴线方向呈β_b角的直线BB，当这一平面或称发生面在基圆柱上作纯滚动时，直线B所绘出的曲面就是渐开线螺旋面，如图7-1所示。则线上任一点都绘出渐开线，这些渐开线合并起来，就成了斜齿轮的齿面，即由绘出的渐开线螺旋面。此渐开线螺旋面与任何一个以OO为轴线的圆柱面的交线都是螺旋线，但在不同的圆柱面上其螺旋角是不同的，直径越大，螺旋角也越大，由图7-2可知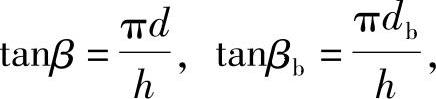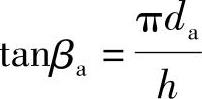，，其中h为导程。

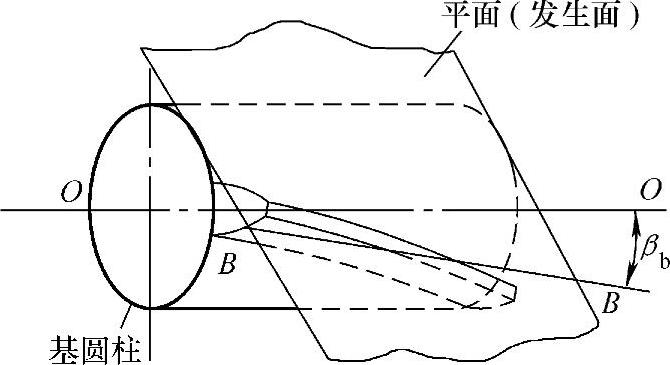
图7-1 斜齿轮齿面的形成

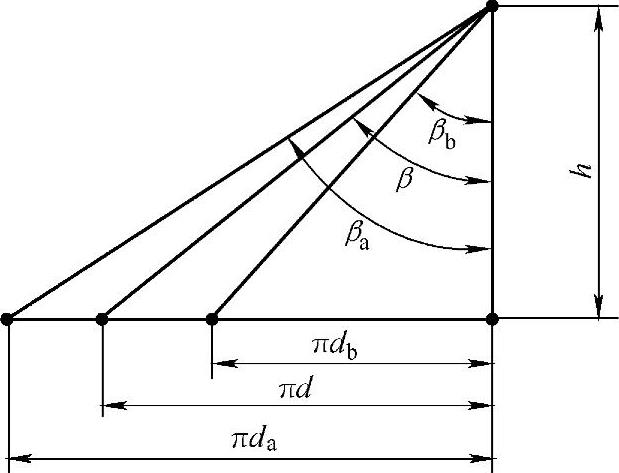
图7-2 斜齿轮的螺旋角

2.渐开线螺旋面的方程式

图7-3中，已知xOy上的一条渐开线KK，当渐开线上的每一点都绕z轴作相同的螺旋运动时，即一方面绕z轴等速转动，同时沿z轴作等速直线运动，就形成一个渐开线螺旋面，即为斜齿轮的齿面。

渐开线上任一点B在xOy平面直角坐标系中的坐标，由图7-4可求得

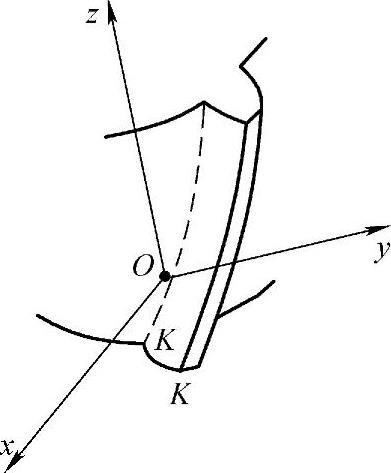
图7-3 渐开线螺旋面

图7-4 渐开线在平面中的坐标

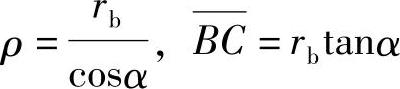
由渐开线的形成及其性质可知，于是可得

式中 r_b——基圆半径。

在求渐开线的直角坐标参数方程时，用∠AOC=φ作参数，φ=α+θ，于是φ=tanα，B点在xOy平面中的直角坐标（x，y）可由下式求得

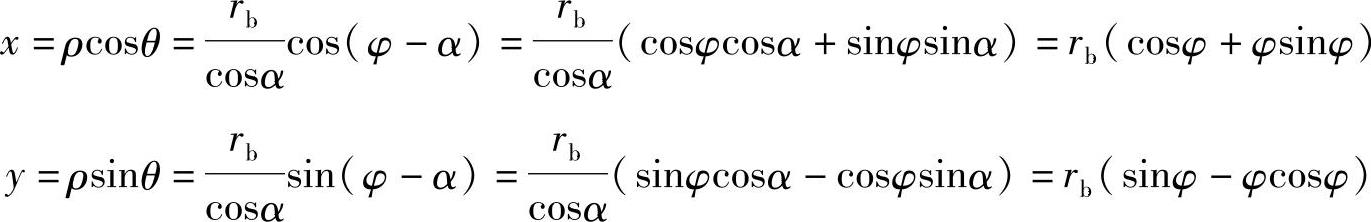
于是渐开线在平面直角坐标系中的方程为

如在空间坐标O_xyz中，上述渐开线的方程可写为(www.xing528.com)

如对应于某一φ=φ₀值的点，则该点在上述渐开线上的方程为

若要得出渐开线螺旋面的方程，必须写出过渐开线上任一点的螺旋线方程，为此先写出过空间任意点的螺旋线方程。设M（x₀、y₀、z₀）是空间坐标Oxyz中任意一点，当其绕z轴作螺旋运动时，其轨迹是一条螺旋线（见图7-5）。过点M（x₀、y₀、z₀）作z轴的垂直平面，其与z轴的交点为O₁，以O₁M为x₁轴正向，以z轴为z₁轴，得一直角坐标系O₁x₁y₁z₁，在此坐标系中，过M点的螺旋线方程为

式中 h——导程；

μ——参数，并假设是右旋螺旋线。

将坐标系O₁x₁y₁z₁与O_xyz进行坐标变换，并经过推导，可得螺旋线在Oxyz中的方程为

图7-5 螺旋线

将渐开线方程式（7-4）代入螺旋线方程式（7-5），即可得到一条通过渐开线上一点的螺旋线的方程，即

μ是方程的参数，对应于μ的一个数值，就有螺旋线上的一个点，对应于不同的φ值，渐开线上有不同的点，就有不同的螺旋线。由这些螺旋线组合起来就形成渐开线螺旋面。代入式（7-6）后，可以得到渐开线螺旋面的方程式，即

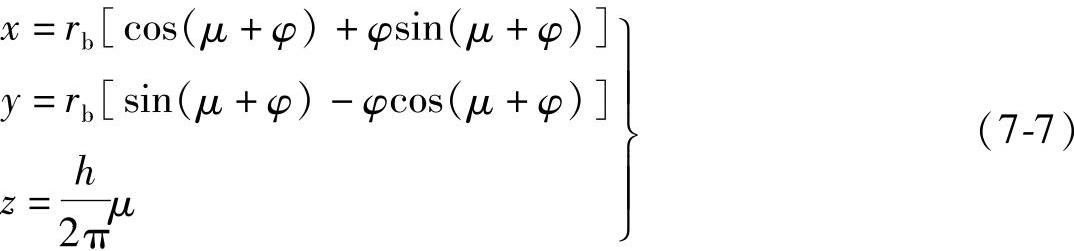
式中 μ、φ——参数。

如果φ=常数，则表示曲面上不同的螺旋线，这些螺旋线的导程h是相同的，但螺旋角不同，其螺旋角为

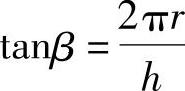
其中r为螺旋线的点到z轴的距离，r越大，螺旋角β也越大。

如果μ=常数，则表示不同位置的渐开线。所以渐开线螺旋面又可以看成是沿一条螺旋排列的渐开线形成的曲面。