外啮合圆柱齿轮变位系数的选择方法优化

1.利用线图选择变位系数

图6-2是用于齿条型刀具加工外齿轮的变位系数选择线图，是由哈尔滨工业大学提出的变位系数选择方法，该方法优于目前所用的其他种类的线图法。该线图用于小齿轮齿数z₁≥12。其右侧部分线图的横坐标表示一对啮合齿轮的齿数和z_Σ，纵坐标表示总变位系数xΣ，图中阴影线以内为许用区，许用区内各射线为同一啮合角（如19°，20°，…，24°，25°等）时总变位系数x_Σ与齿数和z_Σ的函数关系。应用时，可根据所设计的一对齿轮的齿数和z_Σ的大小及其他具体要求，在该线图的许用区内选择总变位系数x_Σ。对于同一z_Σ，当所选的xΣ越大（即啮合角α′越大）时，其传动的重合度ε就越小（即越接近于ε=1.2）。

在确定总变位系数x_Σ之后，再按照该线图左侧的五条斜线分配变位系数x₁和x₂。该部分线图的纵坐标仍表示总变位系数x_Σ，而其横坐标则表示小齿轮z₁的变位系数x₁（从坐标原点向左x₁为正值，反之x₁为负值）。根据x_Σ及齿数比u=（z₂/z₁），即可确定x₁，从而得x₂=x_Σ-x₁。

按此线图选取并分配变位系数，可以保证：

1）齿轮加工时不根切（在根切限制线上选取x_Σ，也能保证齿廓工作段不根切）。

2）齿顶厚s_a>0.4m（个别情况下s_s<0.4m但大于0.25m）。

3）重合度ε≥1.2（在线图上方边界线上选取x_Σ，也只有少数情况ε=1.1～1.2）。

4）齿轮啮合不干涉。

5）两齿轮最大滑动率接近或相等（η₁≈η₂）。

6）在模数限制线（图中m=6.5，m=7，…，m=10等线）下方选取变位系数时，用标准滚刀加工该模数的齿轮不会产生不完全切削现象。该模数限制线是按齿轮刀具GB/T 6083—2001规定的滚刀长度计算的，若使用旧厂标的滚刀时，可按下式核算滚刀螺纹部分长度l是否够用。

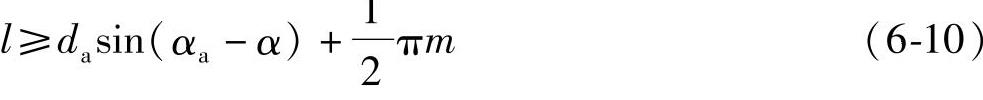
式中 d_a——被加工齿轮的齿顶圆直径；

α_a——被加工齿轮的齿顶压力角；

α——被加工齿轮的分度圆压力角。

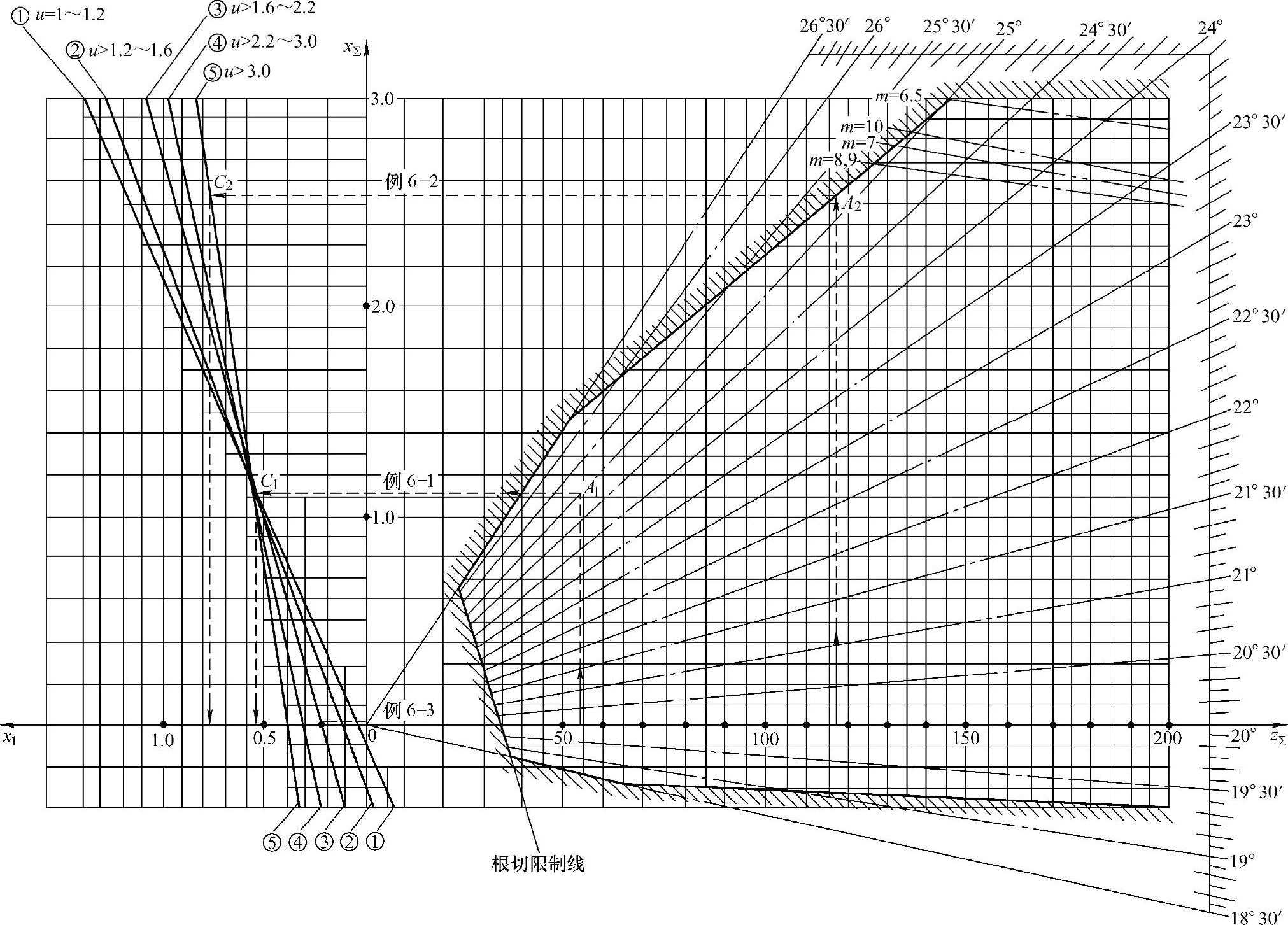
图6-2 选择变位系数线图（h^*_a=1，α=20°）

【例6-1】已知某机床变速器中的一对齿轮，z₁=21，z₂=33，m=2.5mm，α=20°，h^*_a=1，中心距a′=70mm，试确定变位系数。

解 1）根据给定的中心距a′求啮合角α′。

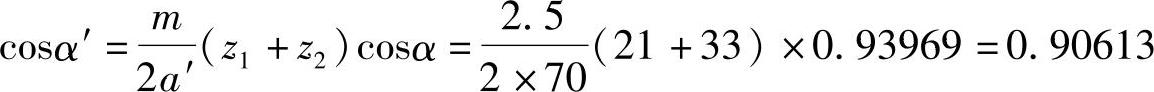
故 α′=25°1′25″

2）在图6-2中，由（0，0）点按α′=25°1′25″作射线，与z_Σ=z₁+z₂=21+33=54处向上引的垂线相交于A₁点，A₁点的纵坐标值即为所求的总变位系数x_Σ（见图中例6-1，x_Σ=1.125），A₁点在线图的许用区内，故可用。

也可以根据求得的α′按无侧隙啮合方程式，算得x_Σ，如图6-2中例题。

3）根据齿数比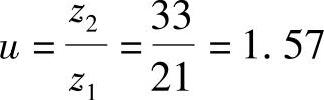，故应按线图左侧的斜线②分配变位系数x₁。自A₁点作水平线与斜线②交于C₁点，C₁点的横坐标x₁即为所求的x₁值，图中的x₁=0.55。故x₂=x_Σ-x₁=1.125-0.55=0.575。

【例6-2】一对齿轮的齿数z₁=17，z₂=100，α=20°，h^*_a=1，要求尽可能地提高接触强度，试选择变位系数。

解 为提高接触强度，应按最大啮合角选取总变位系数x_Σ。在图6-2中，自z_Σ=z₁+z₂=17+100=117处向上引垂线，与线图的上边界交于A₂点，A₂点处的啮合角值，即为z_Σ=117时的最大许用啮合角。

A₂点的纵坐标值即为所求的总变位系数x_Σ=2.54（若需圆整中心距，可以适当调整总变位系数）。

由于齿数比u=z₂/z₁=100/17=5.9>3.0，故应按斜线⑤分配变位系数。自A₂点作水平线与斜线⑤交于C₂点，则C₂点的横坐标值即为x₁，得x₁=0.77。故x₂=x_Σ-x₁=2.54-0.77=1.77。

【例6-3】已知齿轮的齿数z₁=15，z₂=28，α=20°，h^*_a=1，试确定高度变位系数。

解 高度变位时，啮合角α′=α=20°，总变位系数x_Σ=x₁+x₂=0，变位系数x₁可按齿数比u的大小，由图6-2左侧的五条斜线与x_Σ=0的水平线（即横坐标轴）的交点来确定。

齿数比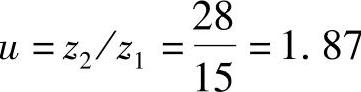，故应按斜线③与横坐标轴的交点来确定x₁，得

x₁=0.23

故 x₂=x_Σ-x₁=0-0.23=-0.23

对于α=25°，h^*_a=1的变位系数选择，按线图6-3进行。

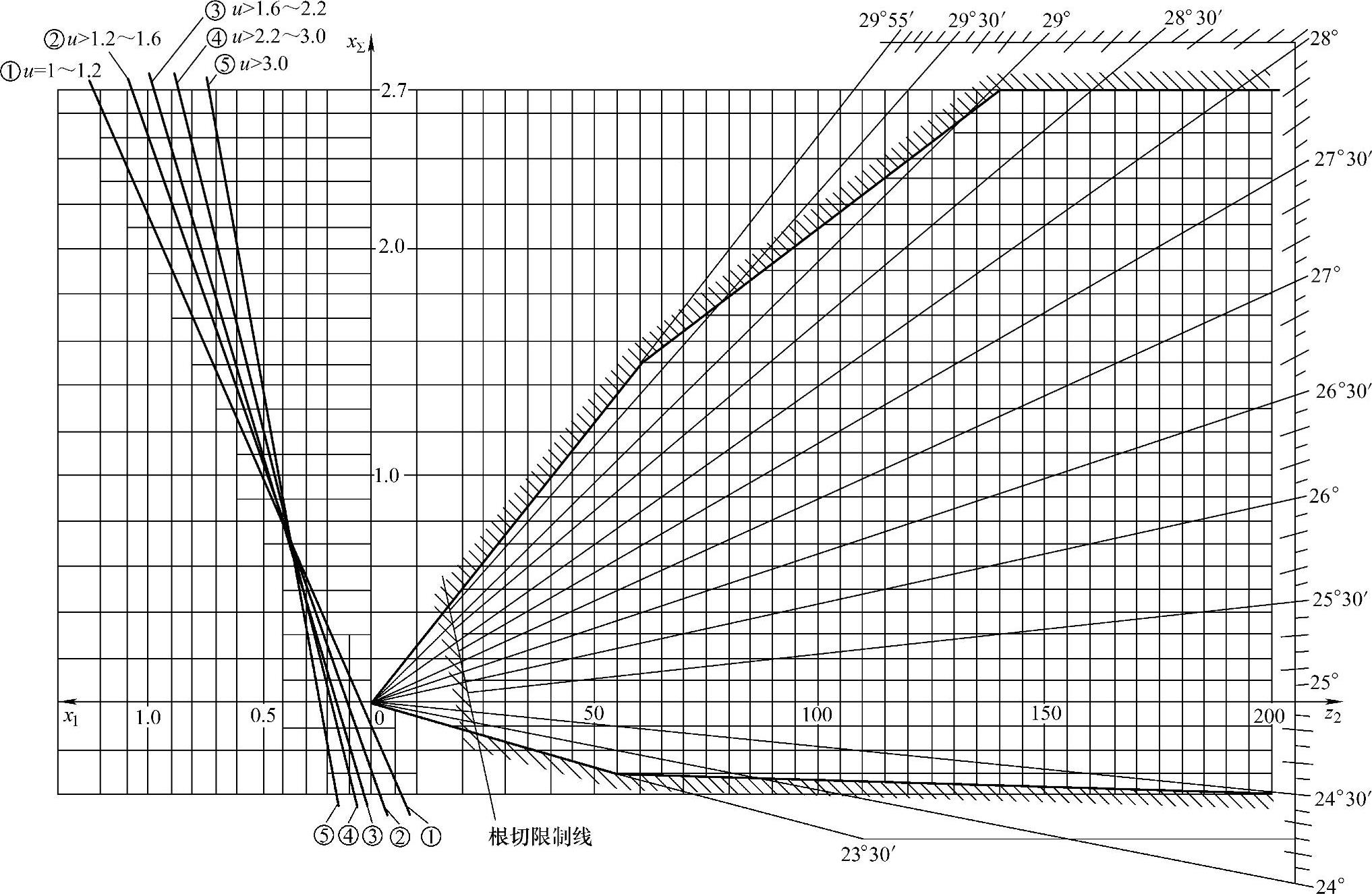
图6-3 选择变位系数线图（α=25°，h^*_a=1）

2.利用封闭图选择变位系数

封闭图是按照给定的齿轮齿数（z₁和z₂）及齿形参数（h^*_a和α），根据上述选择变位系数的限制条件以及一些传动质量指标的要求而绘制的曲线图（见图6-4）。利用封闭图可以根据齿轮传动的不同要求，综合考虑各种性能指标，比较合理地选择变位系数。封闭图比较直观，使用也很方便，但是，要有大量的封闭图才能满足一般工程设计的需要（一般情况下需要数百幅像图6-4那样的图），这是该方法的主要缺点。由于篇幅的限制，本手册无法给出一般常用的封闭图。

（1）封闭图的组成 图6-4为齿条型刀具加工齿轮的典型的封闭图（z₁=34，z₂=38，α=20°，h^*_a=1）。该图中的横坐标代表小齿轮的变位系数x₁，纵坐标代表大齿轮的变位系数x₂。图中有三个封闭区，在封闭区Ⅰ内选择变位系数时，该对齿轮的啮合节点在实际啮合线之内，称为正常许用啮合区；在封闭区Ⅱ和Ⅲ内选取变位系数时，该对齿轮的啮合节点位于实际啮合线之外，故称为节点外啮合区。在三个封闭区内选取变位系数x₁、x₂时，均能满足上述的诸限制条件。

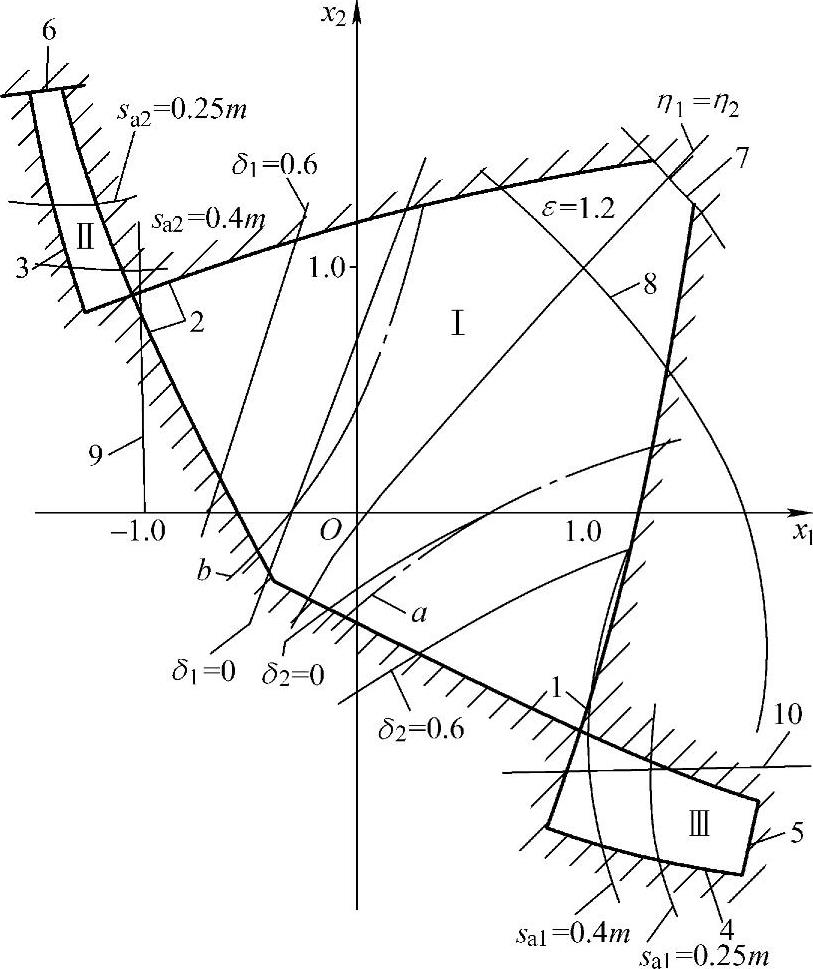
图6-4 选择变位系数的封闭图

图6-4中的封闭区是由下列曲线组成的：

1、2——分别为小齿轮和大齿轮齿根发生过渡曲线干涉的限制曲线；

3、4——分别为小齿轮和大齿轮根切不超过其工作齿廓的限制曲线；

5、6——分别为齿顶厚s_a1=0和s_a2=0的限制曲线；

7、8——分别为重合度ε=1和ε=1.2的限制曲线；

9、10——分别为小齿轮不根切的最小变位系数x_1min和大齿轮不根切的最小变位系数x_2min的限制曲线。

封闭图中还绘出了几种质量指标曲线：

a、b——分别为小齿轮主动或大齿轮主动时，相同材料及热处理的齿轮传动，轮齿等弯曲强度曲线；

η₁=η₂——实际啮合线两端点处，齿根滑动率相等的曲线；(www.xing528.com)

δ₁=0、δ₂=0——节点位于一对齿啮合与两对齿啮合的分界点上的曲线；

δ₁=0.6——节点在小齿轮齿顶与大齿轮齿根接触的双齿对啮合区内，它与

单齿对和双齿对啮合的分界点的距离为0.6m时的曲线；

δ₂=0.6——节点在大齿轮齿顶与小齿轮齿根接触的双齿对啮合区内，它与

单齿对和双齿对啮合区的分界点的距离为0.6m时的曲线；

s_a1=0.25m、s_a2=0.25m——小齿轮、大齿轮齿顶厚为0.25m的曲线；

s_a1=0.4m、s_a2=0.4m——小齿轮、大齿轮齿顶厚为0.4m的曲线。

（2）封闭图的使用方法 在任一封闭图中作出45°斜线1-1、2-2、3-3（见图6-5），这些斜线称为等啮合角线，即在同一条斜线上的不同点选取变位系数时，其总变位系数x_Σ不变，因而其啮合角α′是相等的。若在斜线1-1上选取变位系数时，其总变位系数x_Σ=x₁+x₂>0，为正传动；若在斜线2-2上选取变位系数时，其总变位系数x_Σ=x₁+x₂=0，为高度变位；若在斜线3-3上选取变位系数时，其总变位系数x_Σ=x₁+x₂<0，为负传动。

1）当给定中心距a′时选择变位系数。若给定中心距a′，可按无侧隙啮合方程计算出啮合角α′及总变位系数xΣ，再按算得的x_Σ作出等啮合角线。假如求得的等啮合角线为图6-5中的斜线1-1，在该等啮合角线上的任一点选取变位系数，均可满足中心距a′的要求。

如果既要求中心距为a′，又要求两齿轮的最大滑动率相等，可选斜线1-1与η₁=η₂曲线的交点A为变位点（其变位系数分别为x_1A、x_2A）。

2）当要求接触强度为最高时选择变位系数。一对齿轮传动的啮合角α′越大，其接触强度越高，而啮合角α′越大时，重合度ε就越小。故选择变位系数时，应在保证重合度要求的条件下尽量增大啮合角α′，若要求ε=1.2时使接触强度最高，可作一条45°斜线与ε=1.2曲线相切，其切点即为所要求的变位点（见图6-5中斜线4-4与ε=1.2曲线的切点B）。

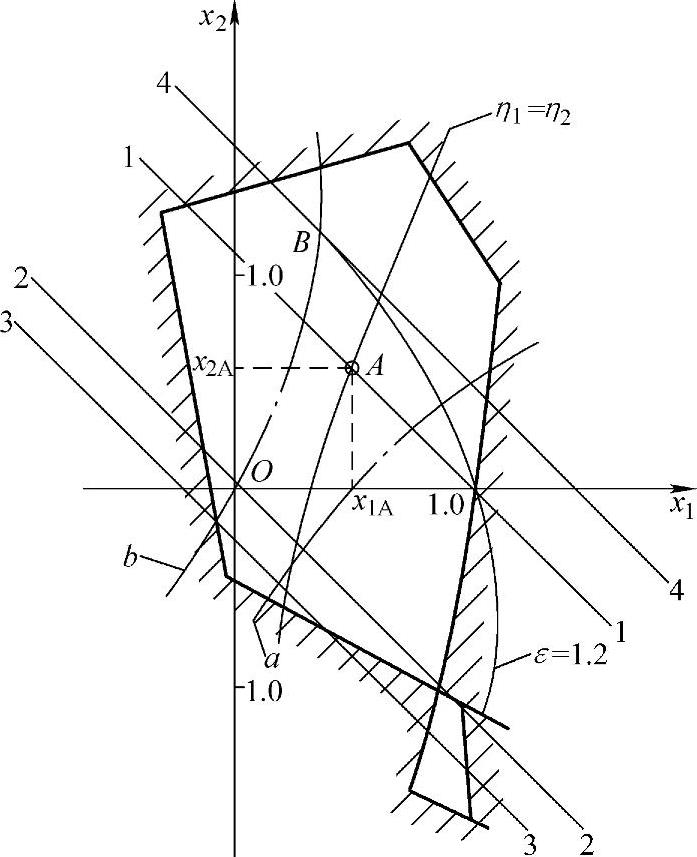
图6-5 用封闭图选择变位系数方法

此外，若要求两齿轮的齿根弯曲强度相等时，变位点应选择在曲线a（当小齿轮主动时）或曲线b（当大齿轮主动时）上。若要求两齿轮具有较高的抗胶合和耐磨损性能时，可在η₁=η₂曲线上选择变位系数，并尽可能地增大啮合角α′。

3）实现节点两对齿啮合或节点外啮合时变位系数的选择方法。

①实现节点两对齿啮合。一般齿轮传动，在节点P处只有一对轮齿啮合，因而在节点（线）附近齿面上的接触应力较大，轮齿的齿面点蚀损坏总发生在节线以下的齿根部分。也就是说，节点是齿面接触强度薄弱处，设法降低节点处接触应力，是提高齿面承载能力的有效方法。

通过适当地选择变位系数，可使节点位于两对齿啮合区，由两对轮齿分担载荷，就可降低节点处的接触应力。一般情况下，这可使接触强度的承载能力提高40%～50%。由于节点处应力减小，还可以降低噪声。通常用这种变位方法，要求齿轮精度要高于7级（GB/T 10095—2008）。

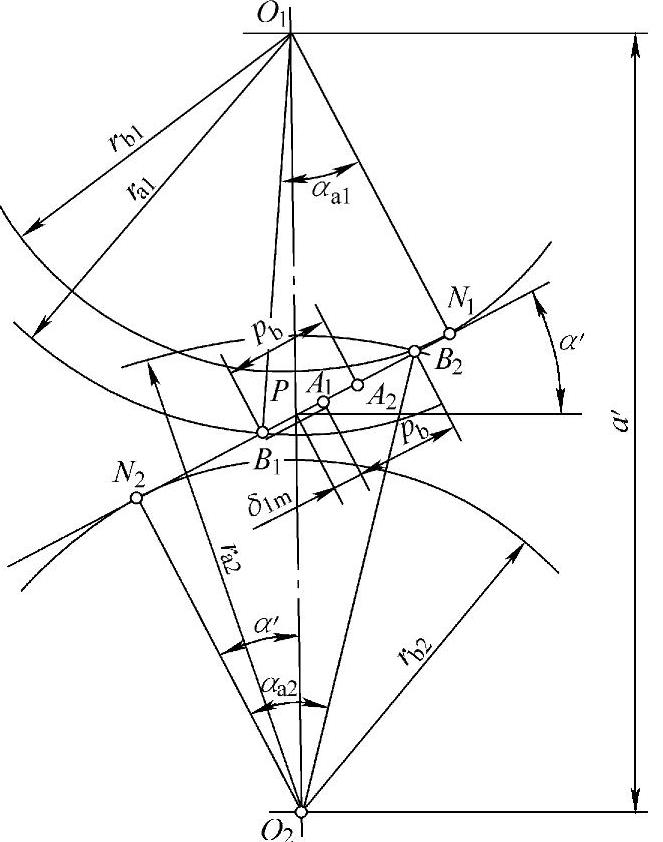
图6-6 节点位于两对齿啮合区的计算图

图6-6表示一对齿轮实际啮合线中的A₁B₁段和A₂B₂段为两对齿啮合区，节点P处于两对齿啮合区内，且位于齿轮z₁的齿顶部。设节点P距离一对齿啮合区的分界点A₁的距离为δ_1m，此时齿轮z₂的齿顶压力角α_a2可用下式求得

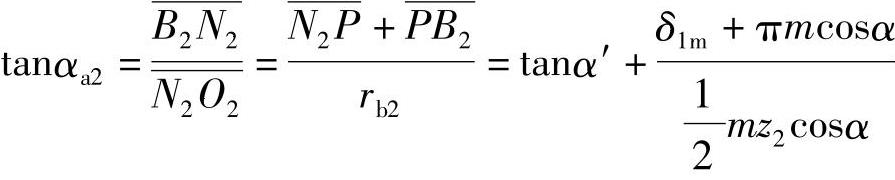
则

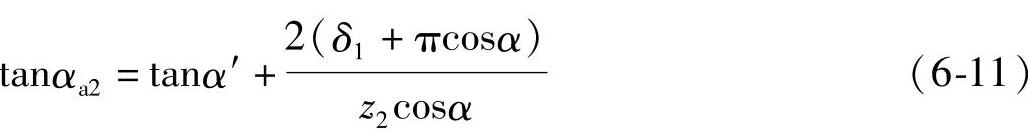
若节点P位于齿轮z₂的齿顶部，且与一对齿啮合区的分界点A₂的距离为δ₂m，则齿轮z₁的齿顶压力角α_a1可按下式求得

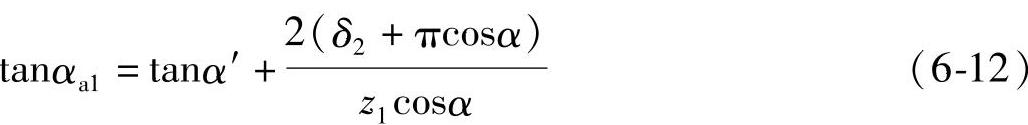
对于齿形参数和齿数z₁、z₂一定的齿轮副，若给定δ₁或δ₂值，并任给出啮合角α′值后，即可由式（6-11）和式（6-12）求出α_a2及α_a1，从而可求出相应的变位系数x₁和x₂，其具体方法和公式如下。

如希望节点P位于小齿轮z₁的齿顶部，而且与一对齿啮合和两对齿啮合的分界点A₁的距离为δ_1m，如图6-6所示，该对齿轮传动的中心距a′为

a′=r_a2+r_f1+c^*m

若将

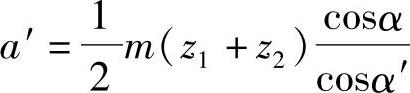
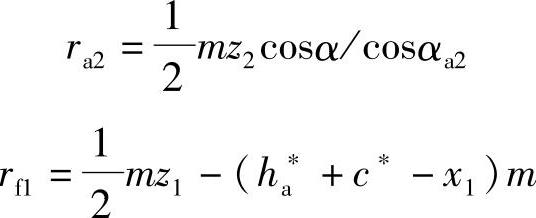
代入上式，整理后可得

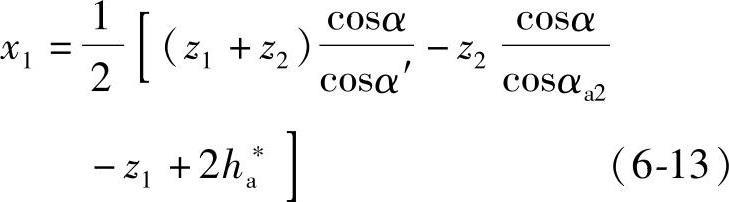
再根据啮合角α′，利用无侧隙啮合方程式，可求得总变位系数x_Σ，从而可得x₂=x_Σ-x₁。

用同样的方法可得节点P位于齿轮z₂的齿顶部，而且与分界点A₂的距离为δ₂m时的变位系数x₁和x₂。

在封闭图中，δ₁=0、δ₁=0.6以及δ₂=0、δ₂=0.6等四条曲线，就是根据上述原理，当给定δ₁或δ₂等于0或0.6时，求得相应的变位系数x₁、x₂之值而作出的。如图6-7所示，若在δ₁=0与δ₂=0两曲线之间的许用区内选取变位系数时，齿轮副的啮合节点P将位于一对齿啮合区中。

若δ₁=0与δ₁=0.6两曲线间的许用区内，选取变位系数时，则齿轮副的啮合节点P将在小齿轮的齿顶部分的两对齿啮合区。若要求节点P位于大齿轮z₂的齿顶部的两对齿啮合区中，变位系数应在δ₂=0与δ₂=0.6两曲线之间的许用区中选取。

②节点外啮合。为了避免或减少齿面在节点附近的点蚀现象，另一种方法是避免齿轮在节点啮合。即适当地选择变位系数，使得啮合节点P位于实际啮合线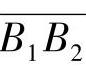之外，于是得名为“节点外啮合”。

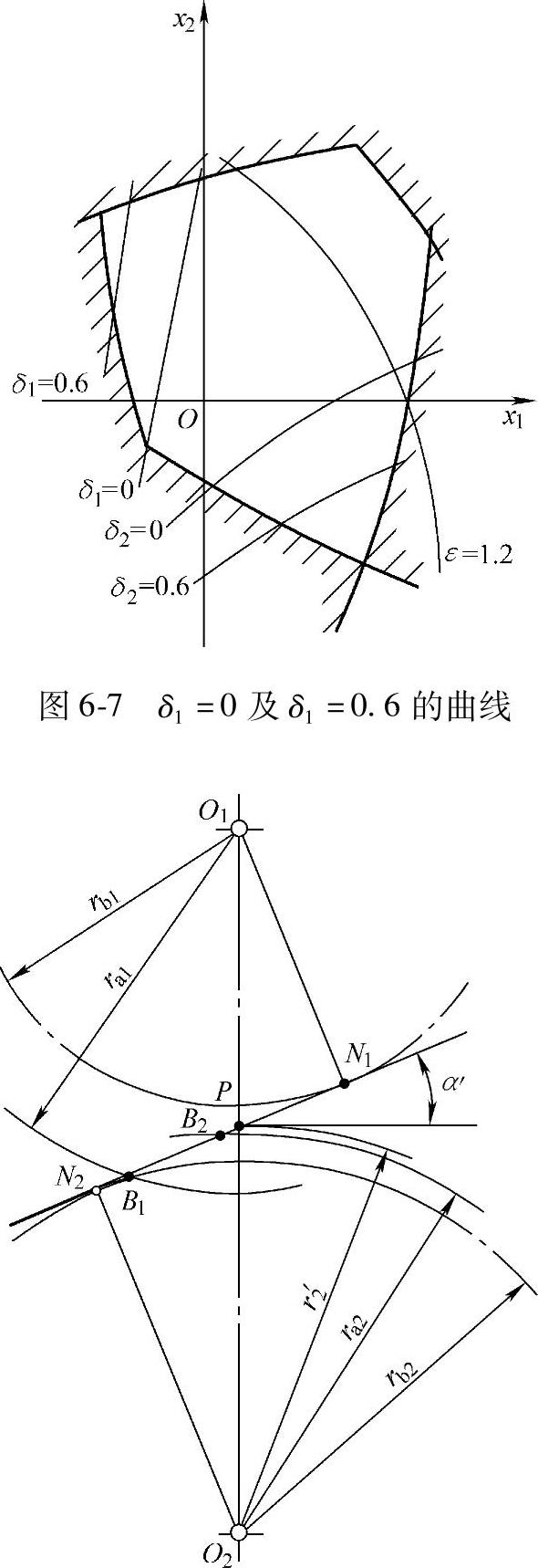
图6-8 节点外啮合图

如图6-8所示，齿轮z₂的齿顶圆小于节圆，即r_a2<r₂′，实际啮合仅在小齿轮z₁的齿顶部分与大齿轮z₂的齿根部分进行。为了保证r_a2<r₂′，齿轮z₂必须为负变位，而且其变位系数x₂必须小于-1。为了不致产生根切，只有当齿轮z₂的齿数较多时，才能实现这种变位。因而，当齿轮的齿数达到一定数值后，在封闭图上才出现一个或两个节点外啮合区，如图6-4所示，封闭区Ⅱ在小齿轮z₁的齿顶啮合的节点外啮合区；封闭区Ⅲ为在大齿轮z₂的齿顶啮合的节点外啮合区。在满足各种限制条件时，如要求s_a2>0.25m，或s_a2>0.4m等，在封闭区Ⅱ或Ⅲ中选取变位系数，即可实现节点外啮合，以提高齿轮的齿面接触强度。

此外，对弯曲强度较有利的高度变位和角度变位系数的选择，也可参考表6-4、表6-5中所列。

表6-4 高度变位齿轮弯曲强度较有利的变位系数x₁

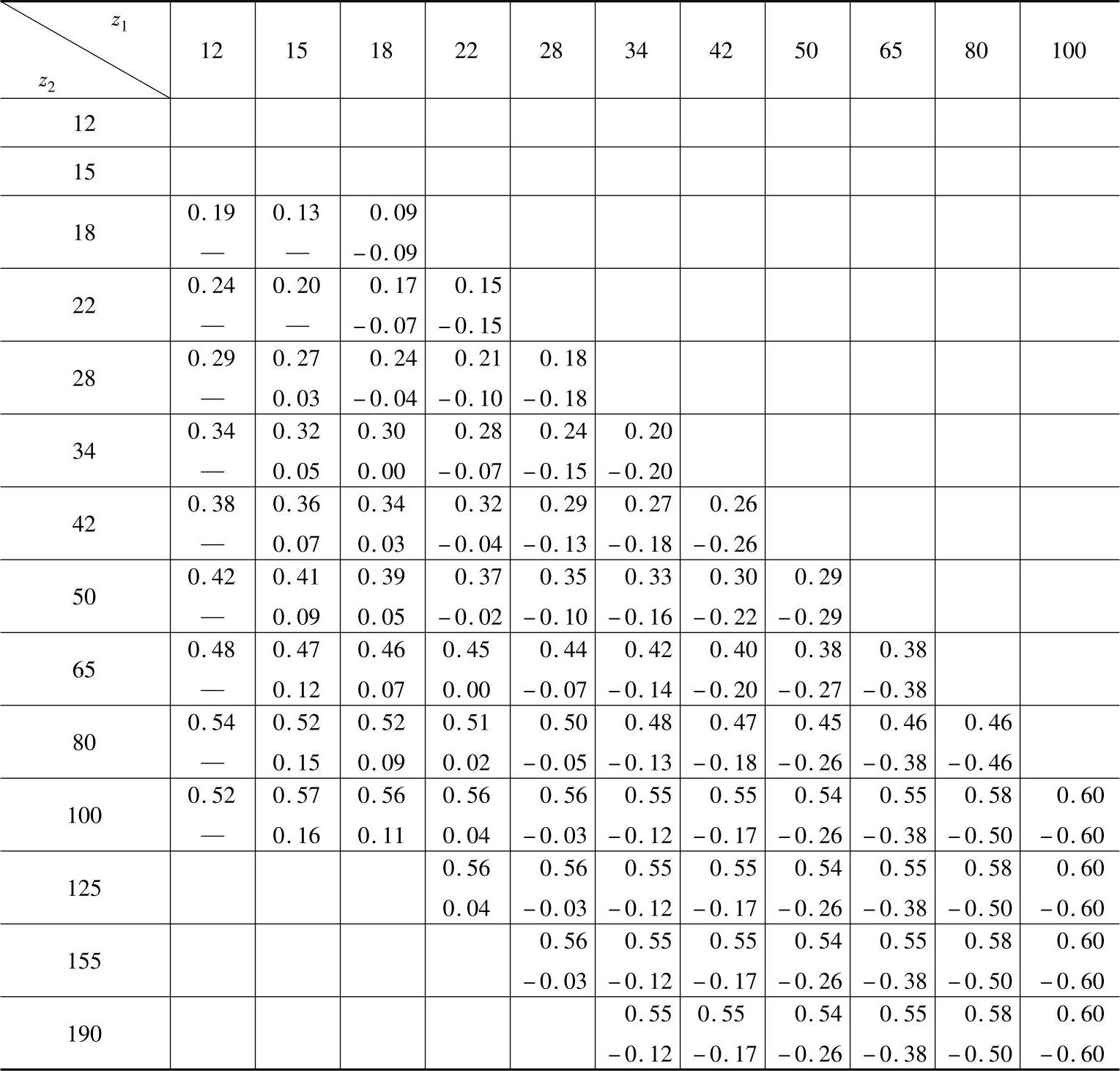
注：表中上面的数字用于z₁齿轮为主动轮时的x₁值；下面的数字用于z₁齿轮为从动轮时的x₁值。

表6-5 角变位齿轮弯曲强度较有利的变位系数x₁及x₂

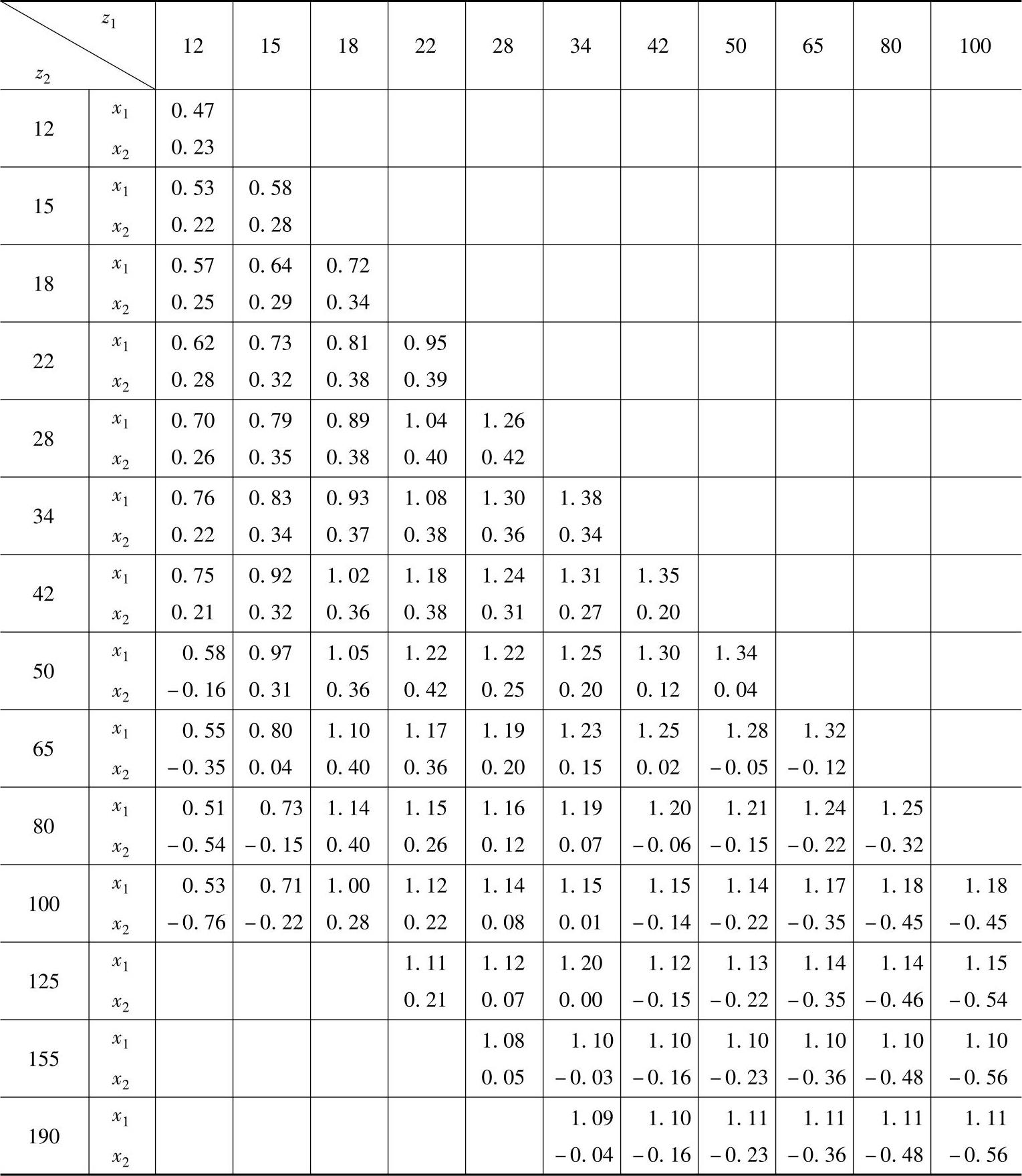
注：齿轮z₁为主动轮时表中的变位系数x才适用。