经理论分析与实验结果表明,齿轮齿廓间的相对滑动越严重,其齿面的磨损也就越严重,也越易产生胶合损坏。因此,为提高齿轮的抗胶合和耐磨损能力,就必须进一步研究齿面间的相对滑动情况及其改善途径。
如图5-4所示,齿轮的一对轮齿在K点啮合时,两轮齿在啮合点的线速度vK1和vK2的大小和方向都不相同。为了保持其高副接触,两齿廓在啮合点K的公法线方向的速度vn应该相等,否则,两齿廓将脱离接触或相互嵌入。因而,在啮合点K处,齿廓切线方向的速度vt1和vt2的大小就必然不等,也就是说,轮齿在啮合过程中,两齿面间存在着滑动速度v21(=vt2-vt1)。
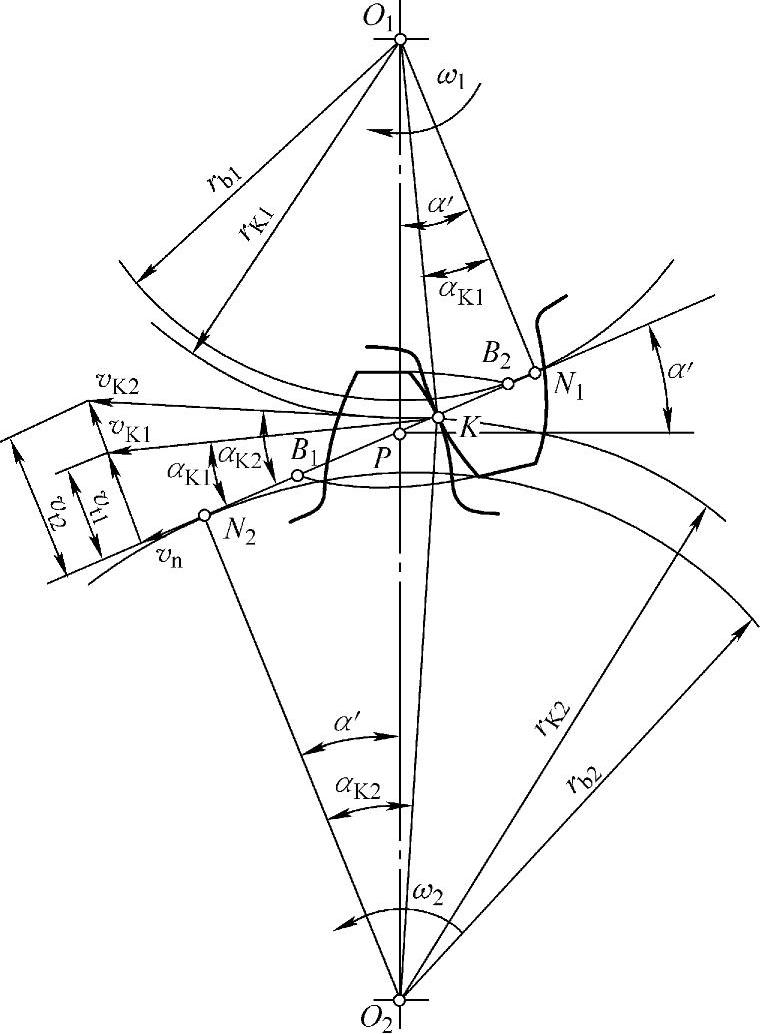
图5-4 滑动率的计算图
通常,用滑动率表示齿面间相对滑动的程度。滑动率,就是在轮齿间接触点K处,两齿面间的相对切向速度(即滑动速度)与该点切向速度的比值,用η表示,即
小齿轮齿面的滑动率η1为

大齿轮齿面的滑动率η2为

很显然,当轮齿在某一点啮合时,其齿面间的滑动速度v21(=vt2-vt1)与vt2(=vt1-vt2)的数值相同而方向相反,因此,该点的滑动率η1与η2的符号也就不同了。下面就讨论滑动率数值的计算。
1.外啮合齿轮传动滑动率的计算
由式(5-8)及式(5-8′)知,为了求得滑动率必须求出切向速度vt1及vt2(见图5-4),即
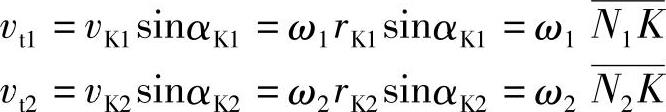
两齿面在K点的相对滑动速度v21为
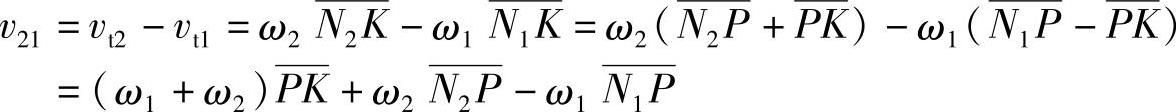
因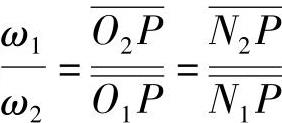 ,即
,即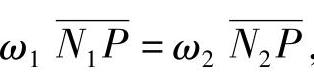 ,则
,则
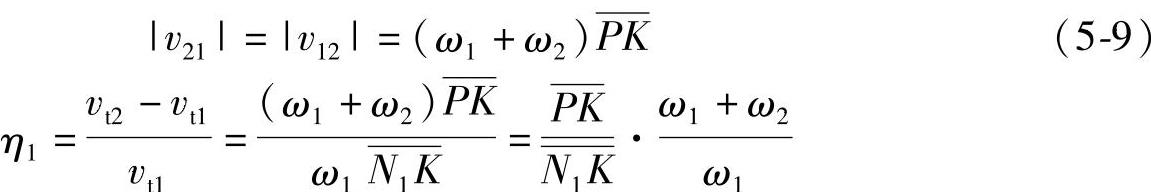
设ω1/ω2=z2/z1=u,称为齿数比,则有

同理
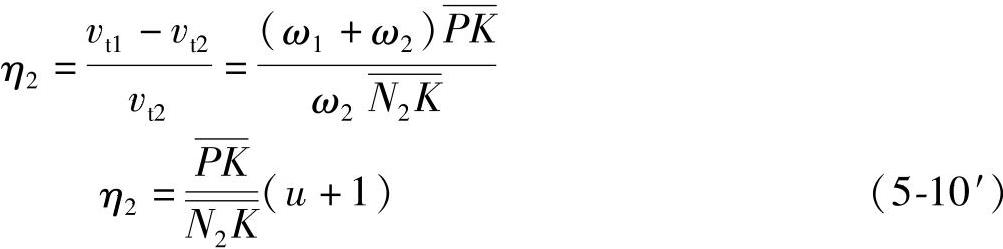
由式(5-10)及式(5-10′)可知,滑动率η1及η2为啮合点K的位置函数,其值随K点位置的变化而变化。
当轮齿在极限啮合点N1啮合时,有
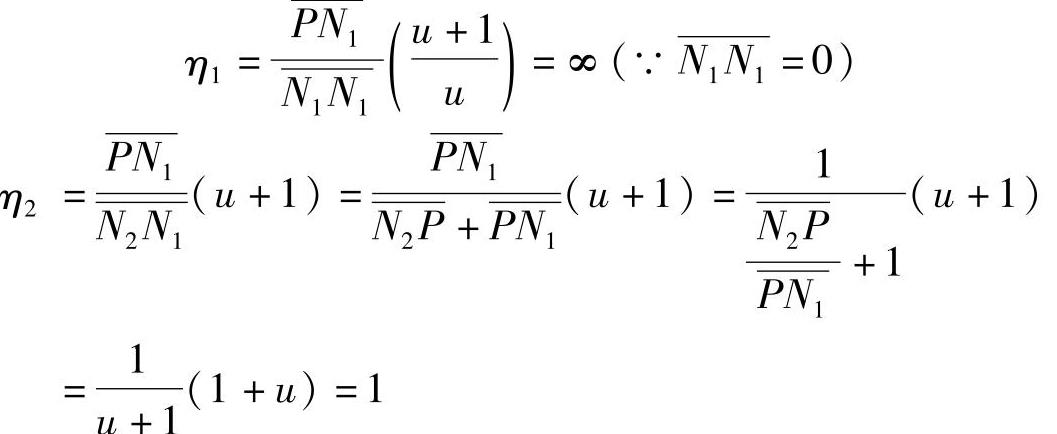
当轮齿在节点P啮合时,有
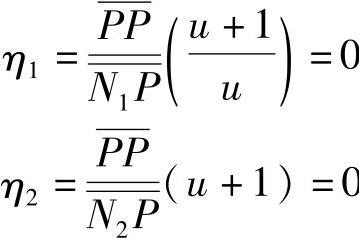
当轮齿在极限啮合点N2啮合时,有
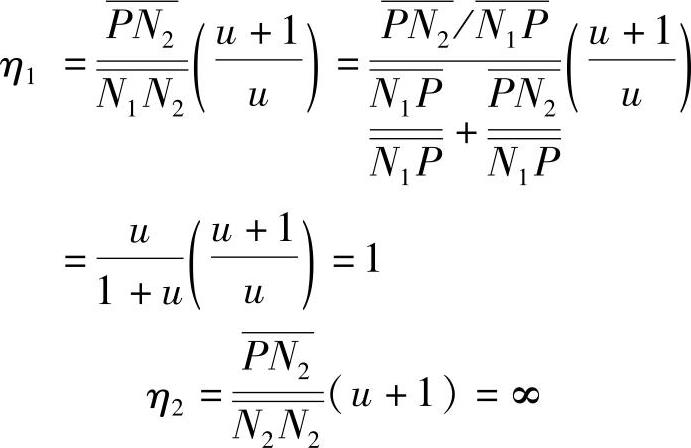
根据上述分析,按式(5-10)及式(5-10′)可以作出如图5-5所示的滑动率变化曲线,其纵坐标为滑动率η,横坐标为啮合线 。对该曲线分析后可得如下结论:
。对该曲线分析后可得如下结论:
①滑动率η是啮合点位置的函数,其值在0~∞之间变化。
②轮齿在节点P啮合时,η1=η2=0,在节点两侧的不同点啮合时,由于滑动速度方向的改变,而使滑动率符号改变。
③轮齿若在极限点N1或N2啮合时,η1或η2将分别达到∞,造成轮齿的严重磨损,故应避免轮齿在极限点啮合。
④实际上,轮齿只能在实际啮合线B1B2上啮合。在B2点啮合时,齿轮1齿根的滑动率η1达到实际的最大值η1max;在B1点啮合时,齿轮2齿根的滑动率达到实际的最大值η2max。
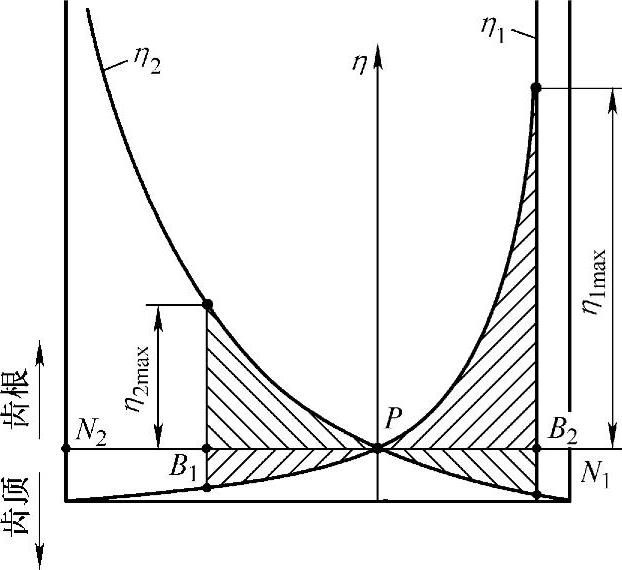
图5-5 外啮合齿轮滑动率曲线
下面讨论实际的最大滑动率η1max和η2max的计算。图5-6表示一对轮齿在B2点啮合时的情况,此时,齿轮1齿根的滑动率达到最大值η1max。由于在B2点啮合,故式(5-10)中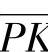 应为
应为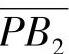 ,
,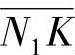 应为
应为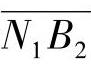 ,则
,则
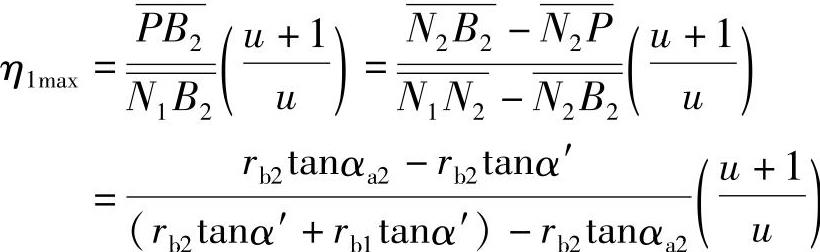
则
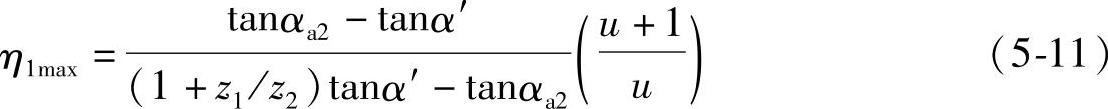
若轮齿在B1点啮合,齿轮2齿根的滑动率达到最大值η2max。同理可求出其值为
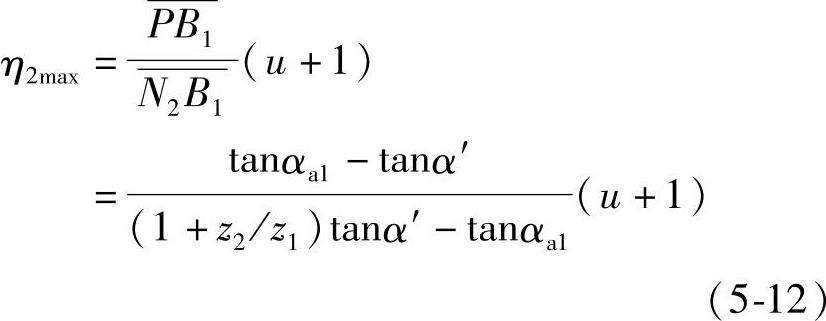
轮齿在不同点啮合时,其滑动率的数值是不同的,在以后的讨论中,若不加特别说明,而讲滑动率η1或η2的具体数值时,均指最大滑动率η1max或η2max。
还应当指出,在相同的工作时间内,大小齿轮参与啮合的次数是不同的。大齿轮2的齿廓参与啮合的次数仅为小齿轮1的齿廓参与啮合次数的1/u倍,所以,在连续工作过程中,大齿轮齿廓的磨损系数应为滑动率的1/u倍。
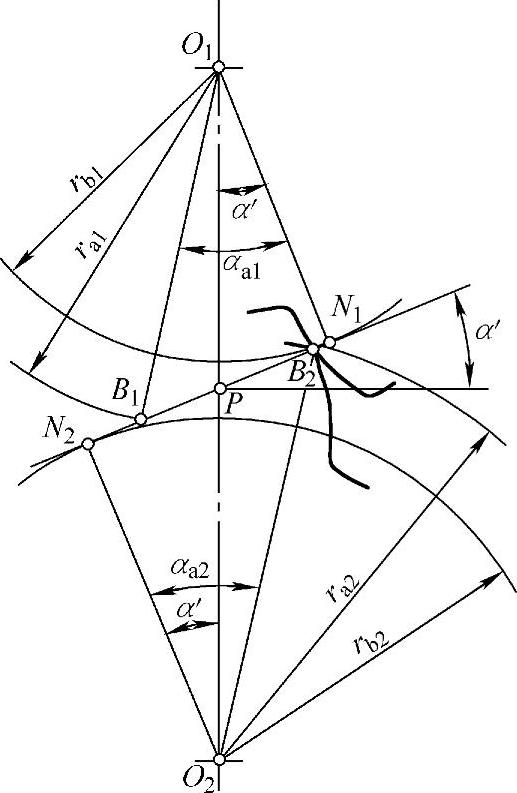
图5-6 最大滑动率的计算图
2.内啮合齿轮传动滑动率的计算
图5-7a为一对内啮合齿轮传动在K点啮合时的情况,根据滑动率的定义及式(5-8)、式(5-9)及式(5-10)的推导,则有
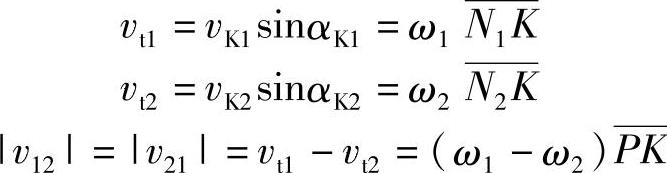
则
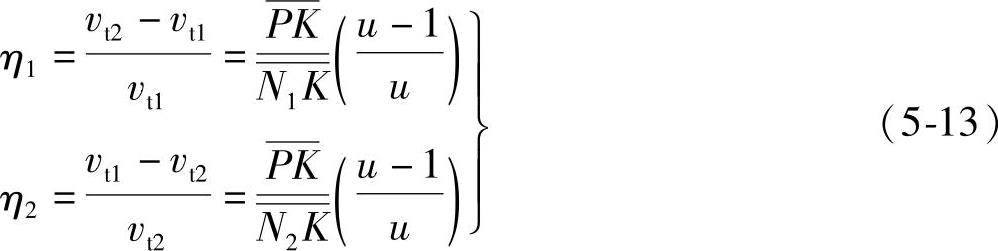
从式(5-13)可知,内啮合齿轮传动的滑动率仍然是啮合点位置的函数,与外啮合相类似。在节点P啮合时,η1=η2=0;在极限点N1啮合时,η1=∞。若以啮合线 为横坐标,可作出如图5-7b所示的内啮合齿轮传动的滑动率曲线。(https://www.xing528.com)
为横坐标,可作出如图5-7b所示的内啮合齿轮传动的滑动率曲线。(https://www.xing528.com)
3.滑动率的调节
(1)滑动率的许用值 滑动率的大小不仅影响齿轮齿面的磨损,而且影响齿面的胶合损坏,因此,为提高齿轮的抗胶合和耐磨损能力,应尽量减少滑动率η的数值。
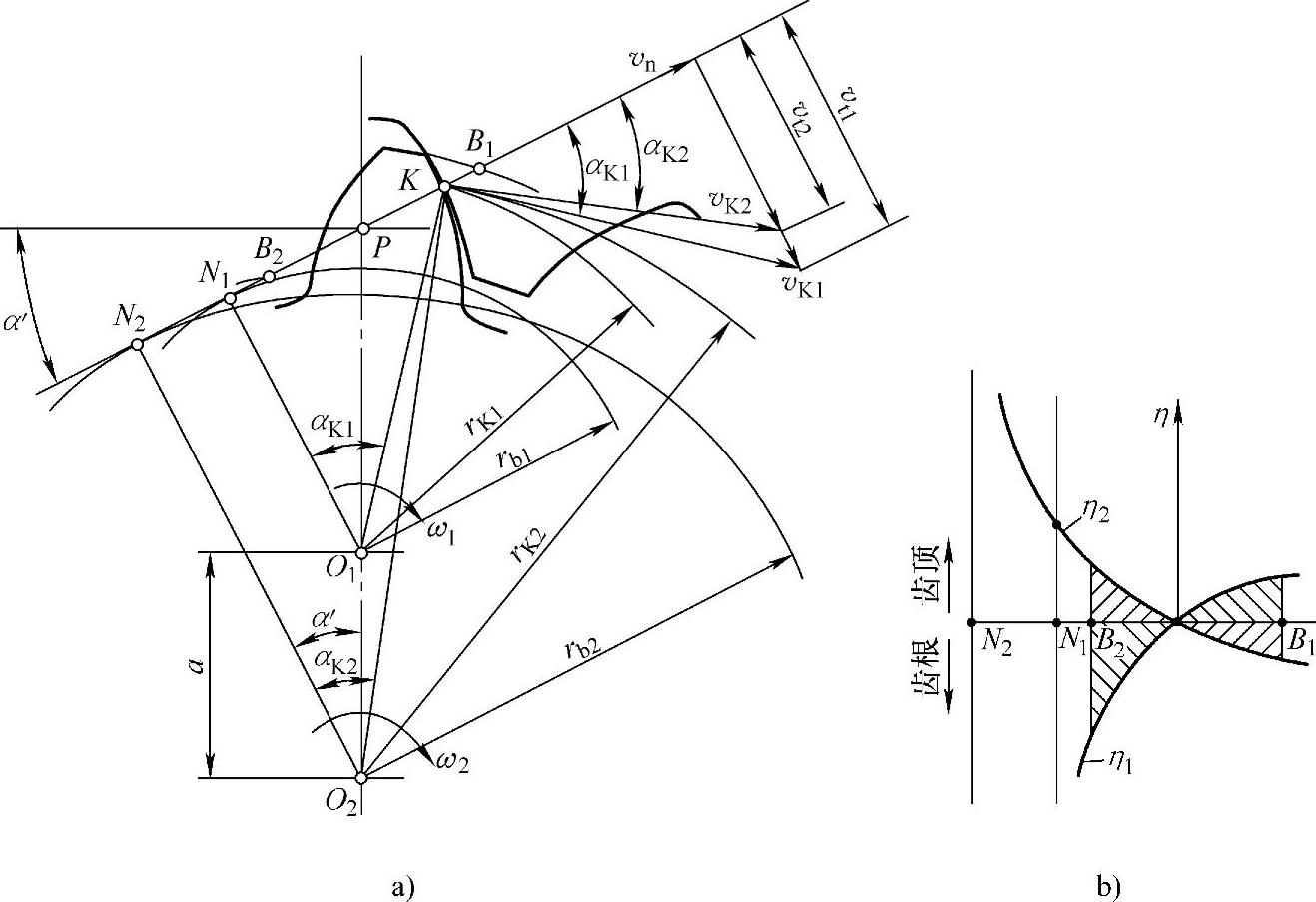
图5-7 内啮合齿轮传动的滑动率
经验表明,齿轮齿廓的滑动率不应大于下列表5-4中数值。
表5-4 滑动率ηmax的许用值

(2)滑动率的调整方法及实例 齿轮齿廓的实际滑动率如图5-5及图5-7b曲线所示。从图中可以看出,轮齿齿根部的滑动率大于齿顶上,而且小齿轮的齿根处B2点的滑动率大于大齿轮在B1点的滑动率。若一对啮合齿轮的齿数差越大时,即齿数比u越大时,B2点就越接近于N1点,则η1max值就越大,以致可能超过上述的许用值。为了满足工业生产的要求,必须设法减小η1max值。较简便的方法是,改变实际啮合线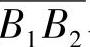 与理论啮合线
与理论啮合线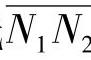 的相对位置,即增大B2点至N1点间的距离,就可以减小η1max值,同时η2max将会有所增加,从而可以调节到η1max=η2max。这可以利用变位齿轮来实现。
的相对位置,即增大B2点至N1点间的距离,就可以减小η1max值,同时η2max将会有所增加,从而可以调节到η1max=η2max。这可以利用变位齿轮来实现。
为保证齿轮传动的中心距不变时,即理论啮合线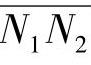 不变时,若减小大齿轮z2的变位系数x2,以减小其齿顶圆直径,可以增大B2点到N1点的距离,即减小η1max;增大小齿轮z1的变位系数x1,以增大其齿顶圆直径,可以使B1点向N2方向移动(对外啮合),使η2max增大,这样就可以调节到η1max=η2max。以下就以一对外啮合齿轮传动为例,研究如何减小η1max,并使η1max=η2max。
不变时,若减小大齿轮z2的变位系数x2,以减小其齿顶圆直径,可以增大B2点到N1点的距离,即减小η1max;增大小齿轮z1的变位系数x1,以增大其齿顶圆直径,可以使B1点向N2方向移动(对外啮合),使η2max增大,这样就可以调节到η1max=η2max。以下就以一对外啮合齿轮传动为例,研究如何减小η1max,并使η1max=η2max。
【例5-2】已知一对外啮合齿轮传动,z1=15,z2=42,ha*=1,α=20°,试求出该对齿轮的最大滑动率η1及η2,并利用变位齿轮调节两滑动率的数值,并使其接近相等。
解 1)两齿轮为标准齿轮时的η1max及η2max。η1max可按式(5-11)计算,η2max可按式(5-12)计算,为此,必须先求出两齿轮的齿顶压力角αa1及αa2,设两齿轮的模数为m,则
da1=mz1+2h*am=17m,db1=mz1cosα=15mcos20°
da2=mz2+2h*am=44m,db2=mz2cosα=42mcos20°
αa1=arccos(db1/da1)=33.989°
αa2=arccos(db2/da2)=26.236°标准齿轮传动的啮合角α′=α=20°,齿数比u=z2/z1=42/15,则
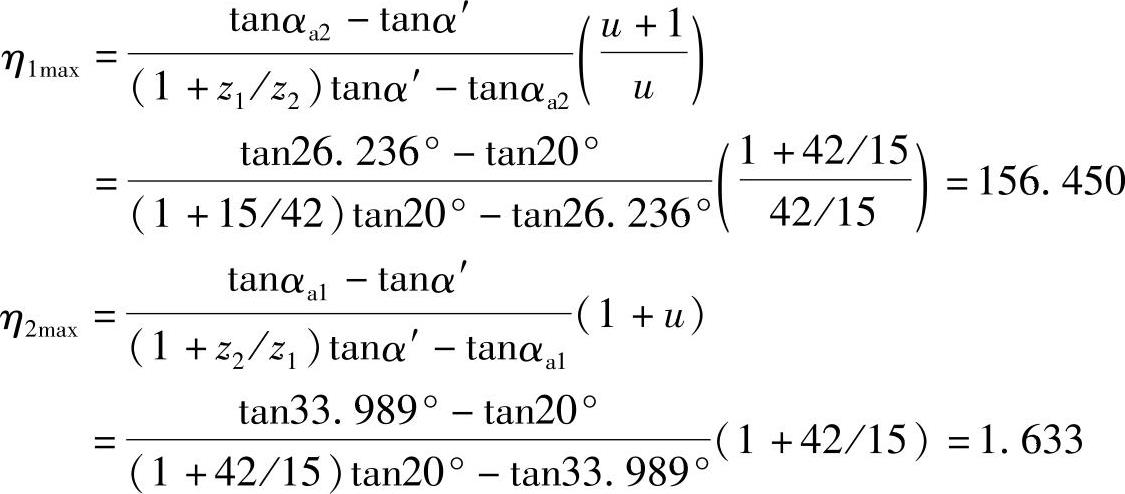
从计算结果可以看出,η1max远远超过了许用值,而相当于η2max的94倍,因而必须设法降低η1max。
2)利用高度变位齿轮降低η1max。根据封闭图,应用滑动率相等原理,初选取变位系数x1=0.32、x2=-0.32,则为高度变位齿轮传动,其啮合角α′=α=20°,变位齿轮的基圆和分度圆,而齿顶圆有所变动,设模数为m,则齿顶圆直径为
da1=d1+2(h*a+x1)m=m(z1+2h*a+2x1)=17.64m
da2=d2+2(h*a+x2)m=m(z2+2h*a+2x2)=43.36m
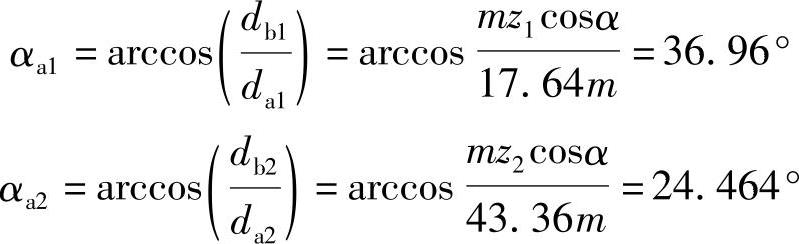

此时η1max比标准齿轮时减小近50倍,仅比η2max大0.828。然而,η2max略有增加。
3)利用角度变位进一步降低η1max及η2max。如果该对齿轮的节圆圆周速度vp>20m/s时,希望ηmax<1.5,为此,还可以利用角度变位来达到这一要求。
查封闭图,若取变位系数x1=0.65、x2=0.92,可以求出其啮合角α′为
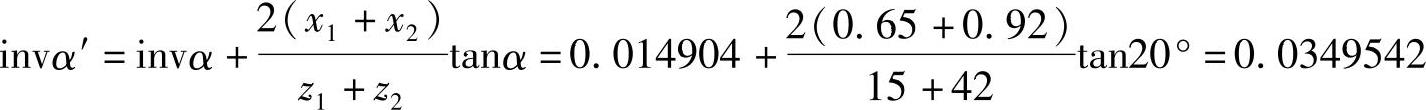
则 α′=26.25°
中心距变动系数
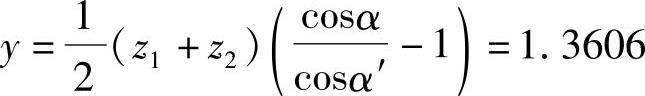
齿顶高变动系数Δy=xΣ-y=x1+x2-y=0.2094
齿顶圆直径da1及da2为
da1=d1+2(h*a+x1-Δy)m=17.8812m
da2=d2+2(h*a+x2-Δy)m=45.4212m
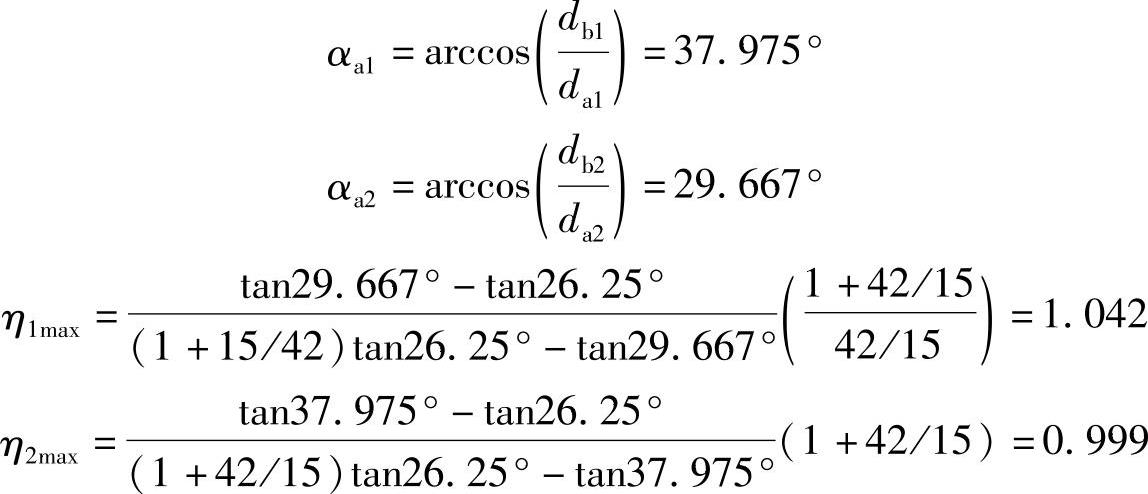
此时,η1max及η2max均小于1.5,可以满足此高速传动的要求,而且η1max与η2max仅差0.043。可见,只要适当地选择变位系数x1及x2,可使两齿轮的最大滑动率接近或相等,即使η1max=η2max。
(3)等滑动率曲线及其特点 由式(5-11)和式(5-12)知,当η1max=η2max时,则
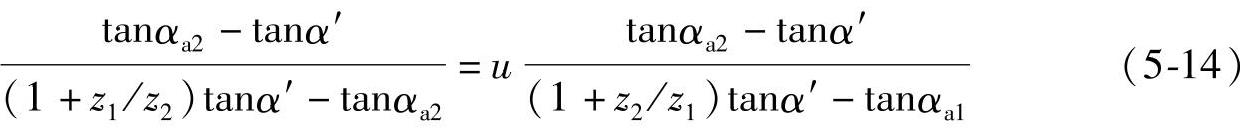
此即为等滑动率方程式。式中齿顶压力角αa1、αa2为齿数z1、z2和变位系数x1、x2的函数。当给定齿轮副的齿数z1、z2后,选定某一啮合角α′的数值,利用无侧隙啮合方程式求得总变位系数xΣ为
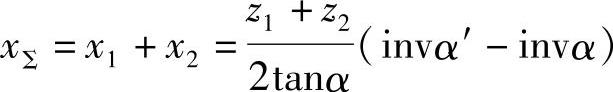
将该式与式(5-14)联立解,可求得给定啮合角α′时的最大滑动率相等的变位系数x1及x2。只要改变啮合角α′的数值(即改变xΣ),即可利用上述公式求出不同啮合角α′时的最大滑动率相等的变位系数x1及x2。这样,就可作出如图5-8的最大滑动率相等的曲线,简称等滑动率曲线或称η1=η2曲线。
现进一步讨论等滑动率曲线的特点。
在图5-9中,绘出了齿数比u=2,而小齿轮齿数z1各不相同时的等滑动率曲线,其中曲线①为z1=12、z2=24的η1=η2曲线;曲线②为z1=25、z2=50时的η1=η2曲线……。可以看出,虽然z1的具体数值各不相同,甚至相差很大(如z1=12与z2=42就差别很大),但只要齿数比u相同(该图中u=2),各η1=η2曲线的基本形状、斜率和截距(见图5-9中的a1、a2…)都相差甚小。
在图5-10中,绘出了z1=17,而齿数比u不同时的等滑动率曲线。其中,曲线①为z1=z2=17的η1=η2曲线(u=1);曲线②为z1=17、z2=25时的η1=η2曲线(u=1.47);曲线③为z1=17、z2=31时的η1=η2曲线(u=1.82)……。可以看出,各条曲线的斜率相差很大,曲线①的截距a1=0,曲线②、③、④的截距a2、a3、a4也都相差甚大。
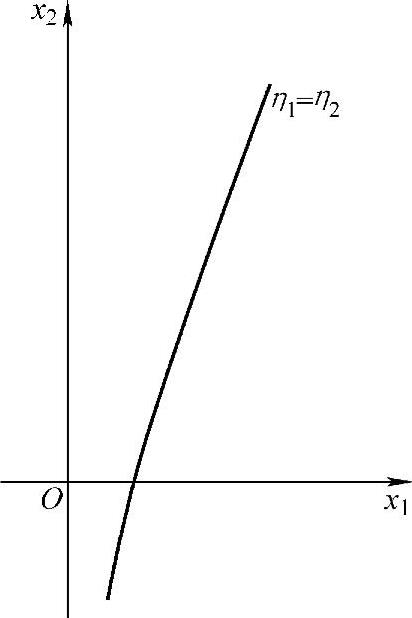
图5-8 等滑动率曲线
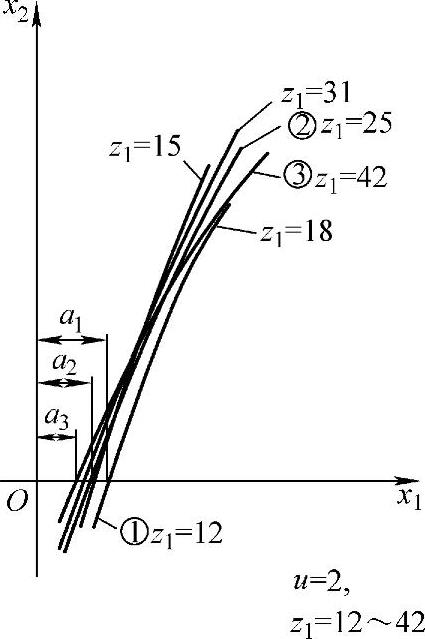
图5-9 齿数比u=2时的η1=η2曲线
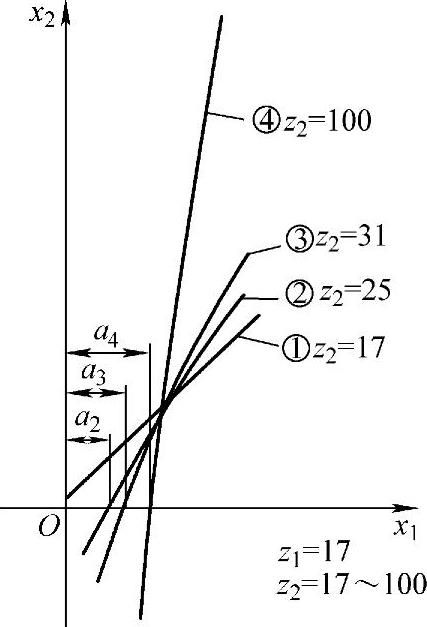
图5-10 z1=17时的η1=η2曲线
由此可知:尽管等滑动率曲线的基本形状随着齿轮副的齿数z1、z2和齿数比u的变化而变化,但其基本斜率主要取决于齿数比u的大小,u越大,斜率就越大。这是等滑动率曲线的一大特点。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




