渐开线齿轮传动的重合度优化方法

1.齿轮传动重合度

一对渐开线齿轮的啮合过程，为了保证齿轮啮合传动的连续性，要求前一对轮齿脱离啮合之前，后一对轮齿应开始进入啮合。如图5-1a所示，前一对轮齿在K点啮合尚未脱开时，后一对轮齿即在B₂点开始进入啮合。根据对轮齿正确啮合条件的分析，图中线段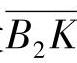既等于齿轮1的基圆齿距p_b1，又等于齿轮2的基圆齿距p_b2，即B₂K=p_b1=p_b2。因此，为了保证齿轮啮合传动的连续性，实际啮合线长度B₁B₂应大于其基圆齿距p_b；否则，若B₁B₂<p_b，如图5-1b所示，当前一对轮齿在B₁点即将脱离啮合时，后一对轮齿还未进入B₂点啮合，这样，当前后两对轮齿交替啮合时必然产生冲击，不能保证传动的平稳性和连续性。所以，一对齿轮连续啮合传动的条件是：两齿轮的实际啮合线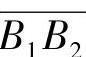的长度应大于（至少等于）其基圆齿距p_b，即B₁B₂≥p_b。通常把这个条件用B₁B₂与p_b的比值ε来表示，ε称为齿轮传动的重合度，即

显然，为了保证齿轮传动的连续性，重合度ε必须大于（至少等于）1，即

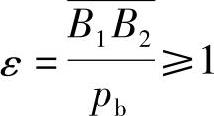
从理论上讲，ε=1就能保证连续传动，但是，考虑到齿轮制造及安装中的误差，应使ε>1。

ε值越大，表明齿轮传动的连续性越好，传动越平稳；但是，ε的数值不可能无限地增大，有一定的限度。在生产中，为了确保齿轮传动的连续性和平稳性，规定了重合度的许用值[ε]，要求

ε≥[ε]

许用的[ε]的大小，随齿轮传动的使用要求及制造精度而定，常用的推荐值见表5-1。

表5-1 推荐的重合度的许用值[ε]

2.重合度ε的计算

根据式（5-1），为了计算出重合度的大小，必须分别算出齿轮的基圆齿距p_b和实际啮合线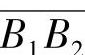的长度。

基圆齿距p_b为

p_b=πmcosα

实际啮合线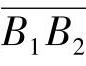的长度可分为外啮合传动和内啮合传动两种情况计算。外啮合齿轮传动，如图5-2a所示。

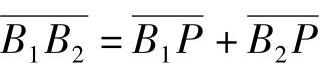
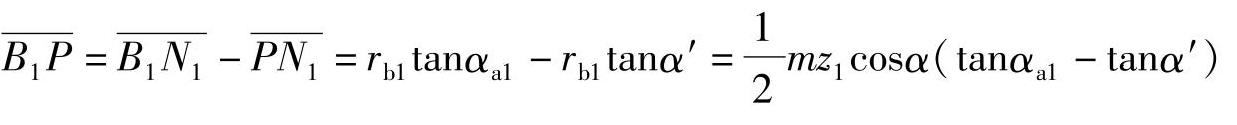
同理

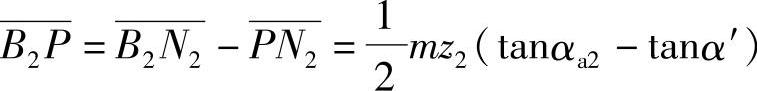
式中 α′为啮合角，α_a1、α_a2分别为齿轮1和齿轮2的齿顶压力角，其值为

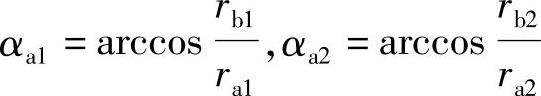
将上式中的B₁P和B₂P之值代入式（5-1），化简后得

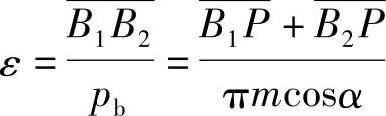
则

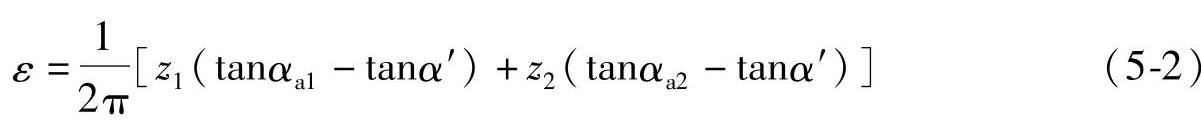
内啮合齿轮传动如图5-2b所示，因

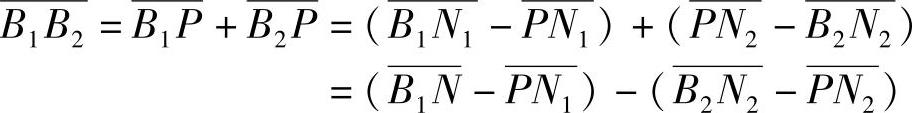
则

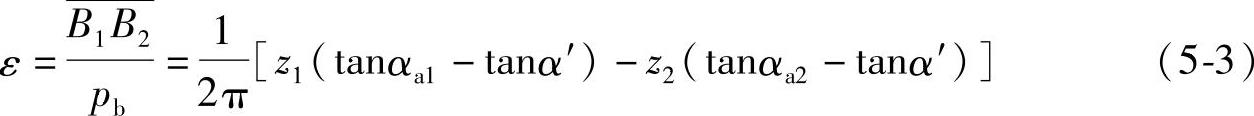
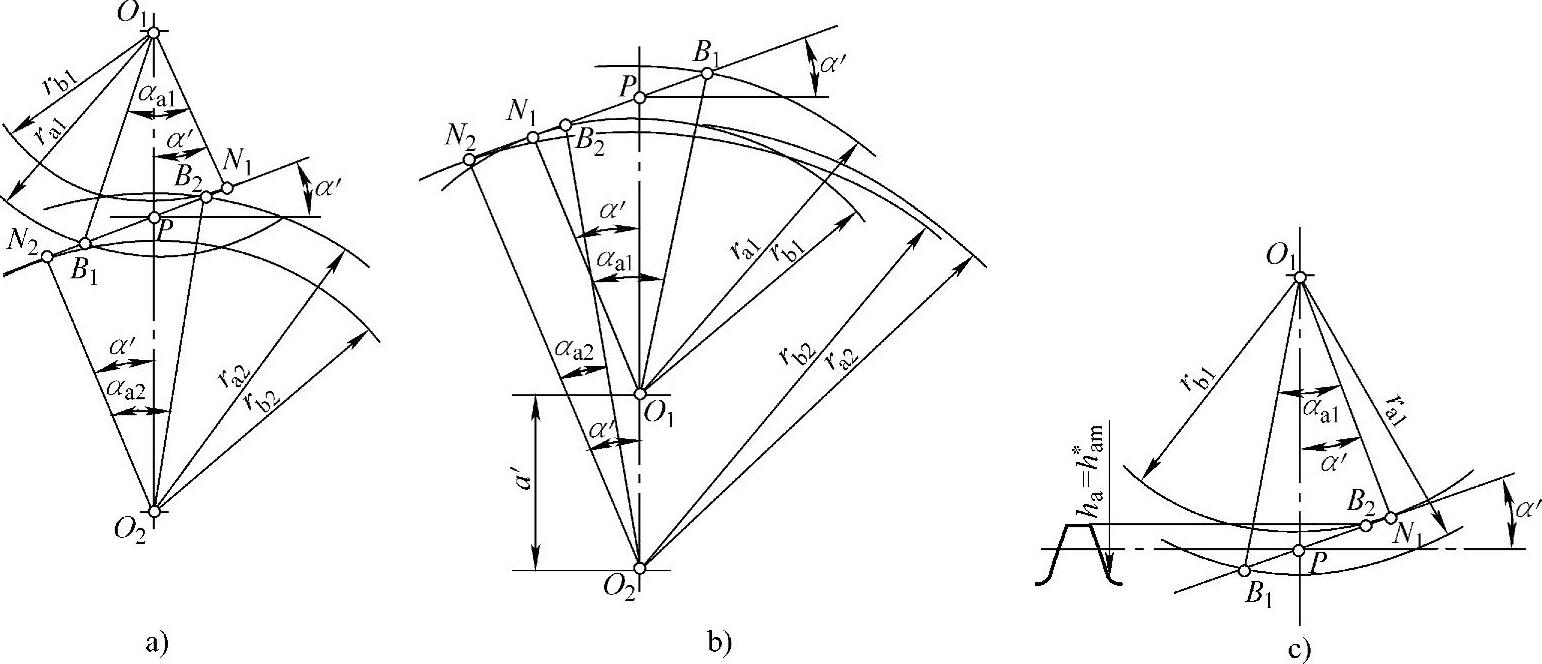
图5-2 渐开线齿轮传动重合度的计算

从式（5-2）和式（5-3）可以看出，重合度ε与齿轮的模数m无关，而随齿数z的增多而增大。若齿轮2的齿数增至无穷大时，即变为齿轮与齿条啮合，如图5-2c所示，此时B₂P为：B₂P=h_a^*m/sinα，因此，齿轮与齿条啮合时的重合度为

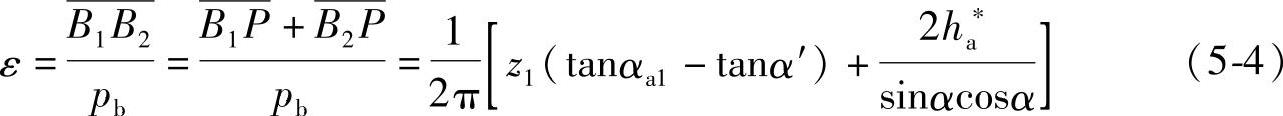
对于一对外啮合齿轮传动，若两齿轮的齿数不断增多，其重合度ε将不断增大，假若两齿轮的齿数均趋近于无穷多时，其重合度必然趋近于一个极限值ε_max，此时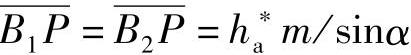，（相当于两个齿条啮合），则

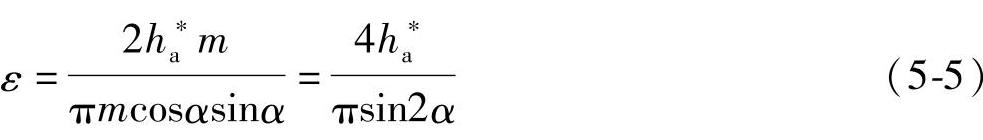
对于不同的分度圆压力角α和齿顶高系数h^*_a，当其啮合角α′大于或等于分度圆压力角α时，ε_max值见表5-2。

表5-2 ε_max值

(www.xing528.com)

从表5-2中可以看出，当α一定时，齿顶高系数h^*_a越大，ε_max就越大；而当齿顶高系数h^*_a一定时，分度圆压力角α越大，则ε_max值越小。因此，为增大齿轮啮合的重合度，就应增大齿顶高系数h^*_a或减小分度圆压力角α。

对于标准直齿圆柱齿轮传动的重合度见表5-3。

此外，从式（5-2）、式（5-3）中还可以看出，在其他条件不变的情况下，当啮合角α′增大时，齿轮传动的重合度ε将减小。在变位齿轮传动中，总变位系数xΣ（=x₁+x₂）增加时，啮合角α′增大，其重合度ε将会减小；当xΣ增大到一定数值后，有可能使ε<1，从而导致传动不连续。因此，对于啮合角α′较大的变位齿轮传动，应校核其重合度。

分度圆压力角α和齿顶高系数h^*_a为定值时的标准齿轮传动，随着齿数z的减少，重合度ε也将减小。对于正常齿的标准齿轮传动，一般情况下，其ε不会小于许用的[ε]，不必验算，如α=20°，h^*_a=1时，z₁=z₂=8，ε=1.307；z₁=z₂=10时，ε=1.369。而对于短齿齿轮传动，当其齿数较少时，需要验算重合度ε，如α=20°，h^*_a=0.8，z₁=z₂=14时，ε=1.218；z₁=z₂=10时，ε=1.145；z₁=z₂=8时，ε=1.096。

当ε=1时，表示齿轮传动在整个啮合过程中，只有一对齿在啮合。对于正常齿的标准齿轮传动，重合度ε总是小于2的数。例如ε=1.5表示什么意义呢？

表5-3 标准直齿圆柱齿轮传动的重合度

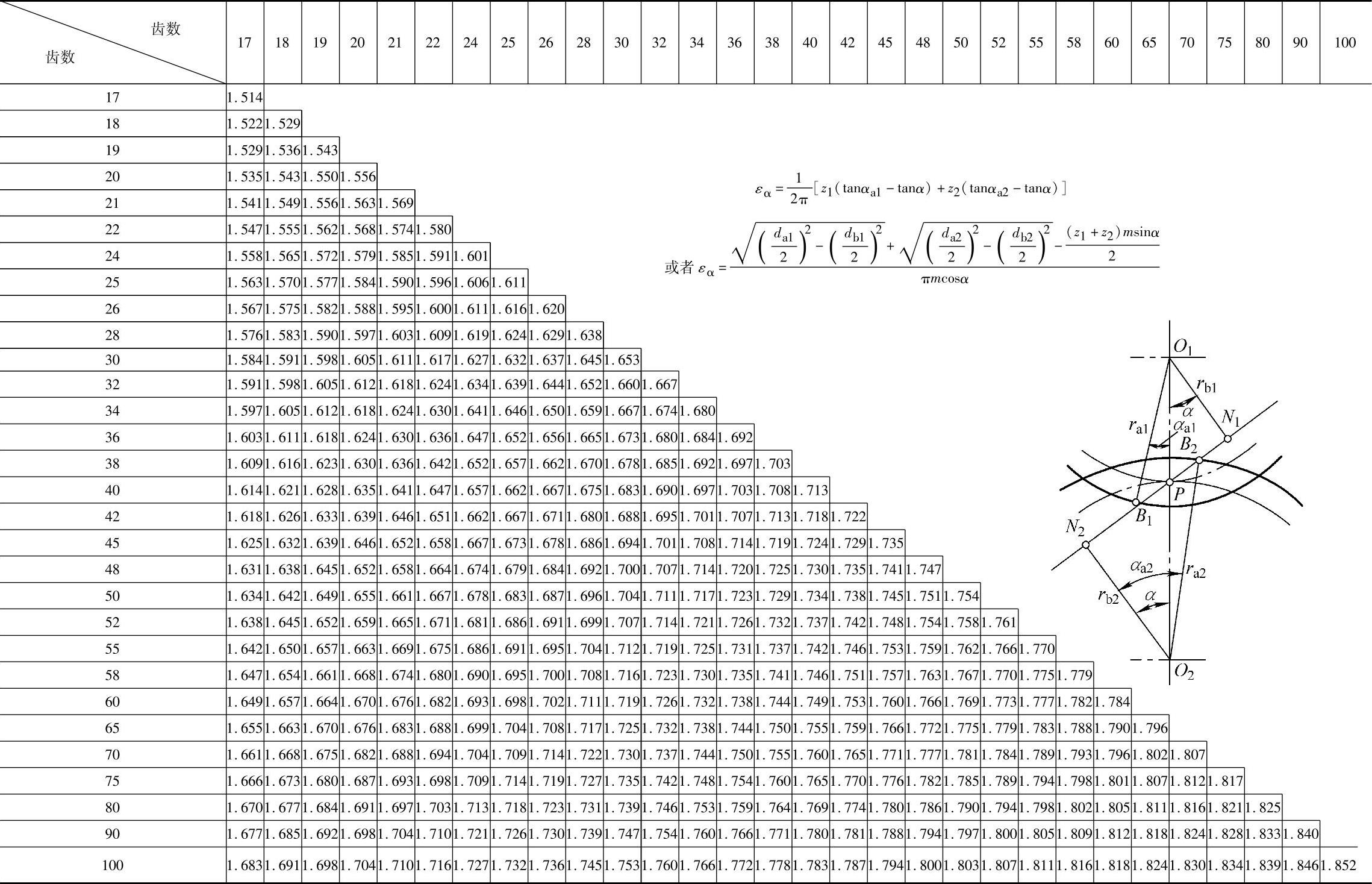
即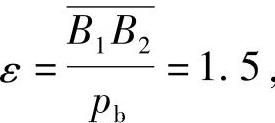，实际啮合线长度B₁B₂=1.5p_b，如图5-1所示，自B₂点量取B₂K=p_b，则B₁K=0.5p_b；反之，若从B₁点量取B₁K′=p_b，则B₂K′=0.5p_b。从齿轮啮合过程可以看出，在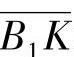和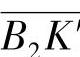两段啮合线内将有两对轮齿在啮合，称为双齿对啮合区；而在KK′区段内，只有一对轮齿在啮合，称为单齿对啮合区。一般情况下，啮合节点P位于单齿对啮合区内。

增大重合度ε，不仅可以提高齿轮传动的平稳性，还可以提高齿轮传动的承载能力。例如ε≥2时，将有两对轮齿承担载荷，可以减小轮齿应力。

3.重合度ε的简便计算法

在设计变位齿轮传动时，往往需要考虑重合度ε的限制来选取变位系数。有时在强度计算时，需要知道重合度的具体数值，这可以根据给定的齿数、齿形参数和变位系数，用式（5-2）或式（5-3）、式（5-4）进行计算，还可以利用图5-3查出ε_α值而后进行计算。

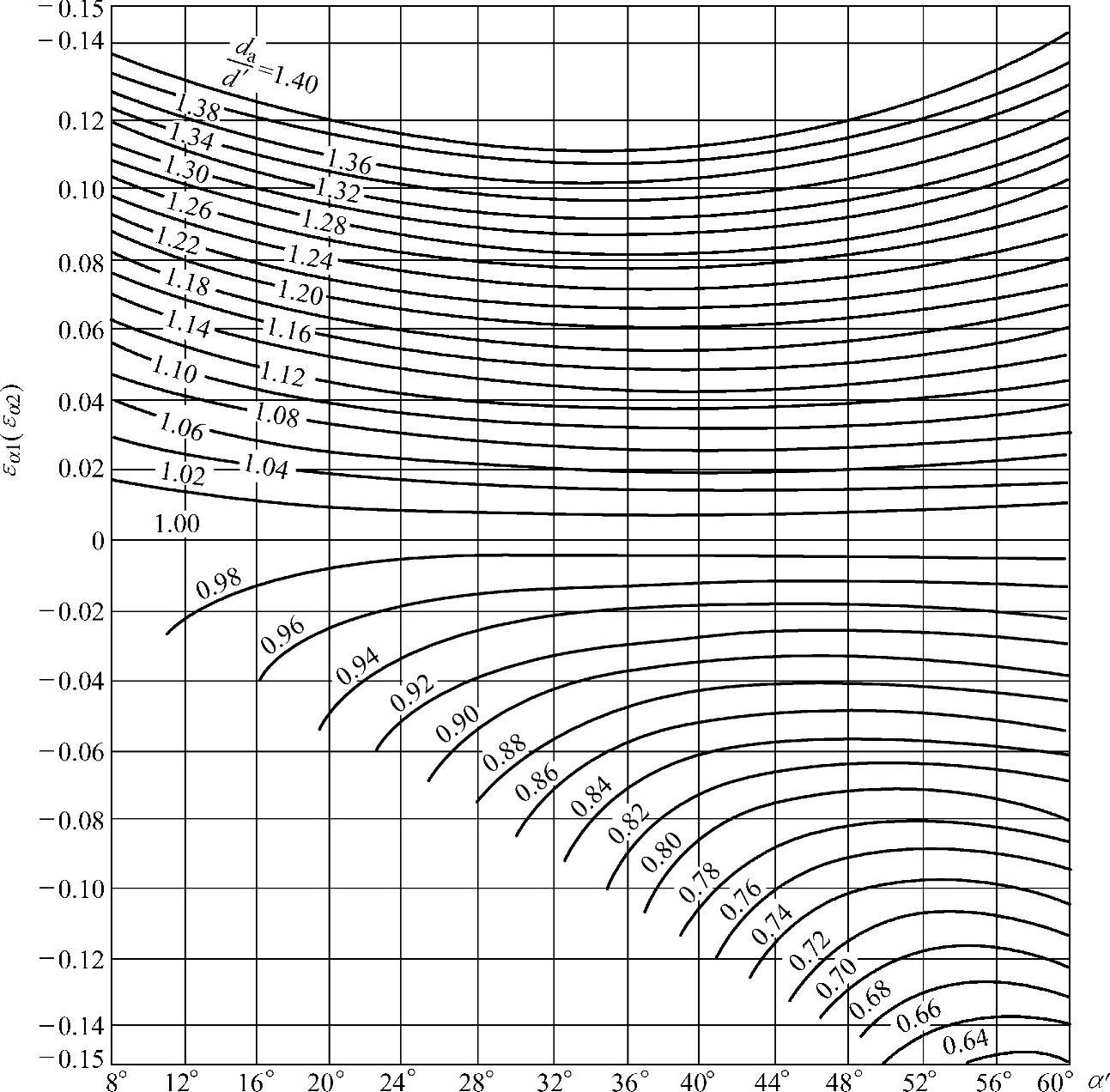
图5-3 重合度计算线图

现对图5-3作图原理说明如下。

将式（5-2）、式（5-3）合并可得

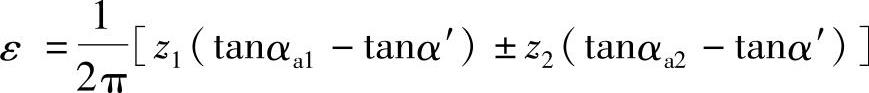
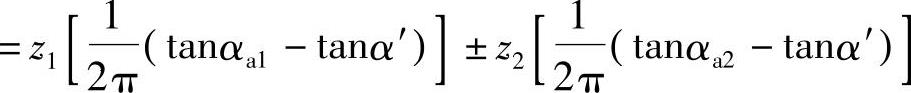
则

ε=z₁ε_α1±z₂ε_α2 （5-6）

式中

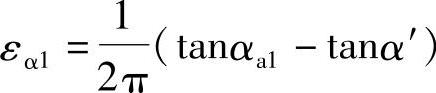
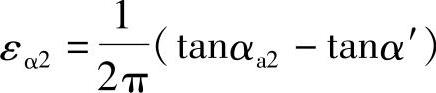
“+”号用于外啮合，“-”号用于内啮合。可见，不论外啮合还是内啮合，其ε_α1或ε_α2的含义是相同的，可归结为

ε_α值仅与齿顶压力角α_a和啮合角α′有关，而与齿数z₁、z₂无关；只要求出齿轮传动的啮合角α′和齿顶压力角α_a，ε_α值就确定了。而

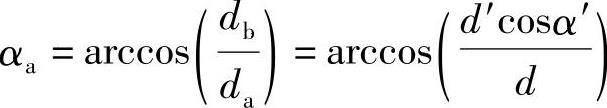
式中 d′——节圆直径；

α′——节圆压力角，即啮合角。

因此，对于一定的啮合角α′值，可按齿顶圆直径d_a与节圆直径d′的比值从图5-3中查出ε_α值，再将其代入式（5-6）计算重合度ε。

【例5-1】z₁=z₂=14，α=20°，h^*_a=0.8的一对标准齿轮传动，试确定其重合度。

解 因为是标准齿轮传动，故啮合角α′=α=20°，d′=d=mz，d_a=d+2h^*_am。假设模数m=1，则d′=mz=14mm。

d_a=mz+2h^*_am=14+2×0.8×1mm=15.6mm则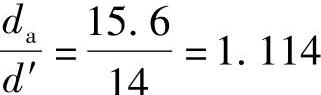，由图5-3查得ε_α=0.043。

于是

ε=z₁ε_α1+z₂ε_α2=14×0.043+14×0.043=1.204

若按式（5-2）计算，ε=1.218，可见，图算法与精确计算的结果基本是一致的。

4.重合度对齿轮传动噪声的影响

由实验研究结果表明，齿轮啮合传动的噪声随着重合度的增大而降低。Nie-mann等关于直齿圆柱齿轮研究噪声的实验结果认为：重合度ε=2时，噪声级数将急剧地减小；当重合度超过2到2.2时，噪声级数又重新增加。因此，为了降低齿轮传动的噪声，应尽可能地增大重合度ε，并使其尽量接近ε=2。