插齿刀加工齿轮及计算方法

由上述可知，插齿刀相当于变位齿轮，所以用插齿刀加工齿轮时，可以认为是一对齿轮在进行无侧隙的啮合。用同一把刀可以加工不变位的齿轮，也可加工不同变位量的齿轮。

设插齿刀的模数、齿形角、齿数和变位系数分别为m、α、z₀及x₀。因为插齿刀在磨损后可以重新刃磨后使用，所以每次刃磨后，其变位系数x₀也将改变，其值可按下式求得：

式中 Δa——插齿刀上所分析的截面与原始截面O—O的距离，如图4-2所示；

α_z——插齿刀齿顶刃后角。

但在一般情况下，由于不知道原始截面的位置，Δa不易求得，因此，在用插齿刀切削齿轮的计算时，为了了解所用插齿刀的磨损程度，可测出插齿刀切削剖面的顶圆半径r_a0，然后根据r_a0计算出变位系数x₀。由前知插齿刀顶圆半径为：

由此可得插齿刀的变位系数x₀为：

加工外齿轮时，插齿刀和被加工齿轮z啮合时的方程式，即根据无侧隙啮合方程式为：

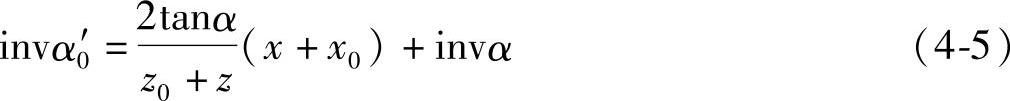
式中 z——被加工齿轮的齿数；

x——被加工齿轮的变位系数；

z₀——插齿刀齿数；

x₀——插齿刀的变位系数；

α₀′——插齿刀加工齿轮时的啮合角。

加工外齿轮时，插齿刀与齿轮的中心距为：

(www.xing528.com)

插齿刀与齿轮的中心距变动系数为：

若已知被加工的外齿轮齿数z、模数m、变位系数x、压力角α，当选用齿数为z₀、变位系数x₀的插齿刀加工时，则其啮合角应按式（4-5）计算。加工时，插齿刀与齿轮的安装中心距a₀，则按式（4-6）计算。

加工齿轮时，由于插齿刀的变位系数x₀不同，加工出的齿轮的齿根圆直径是变化的，即齿轮的顶隙是变化的，加工时，齿轮的齿根圆半径为：

r_f=a₀-r_a0 （4-8）

式中 r_a0——插齿刀顶圆半径，由下式计算

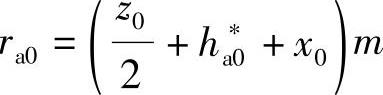
将a₀和r_a0代入r_f，得到加工时的齿根圆半径

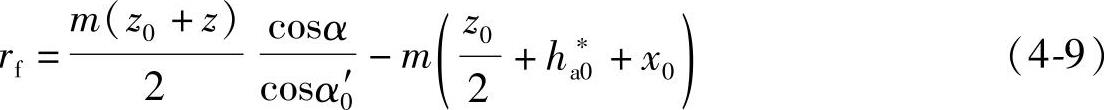
而计算的齿轮齿根圆半径为：

式中 z，x——齿轮齿数及其变位系数。

取插齿刀的齿顶高系数h_a*0=h_a*+c*，将r_f与r′_f进行比较，得

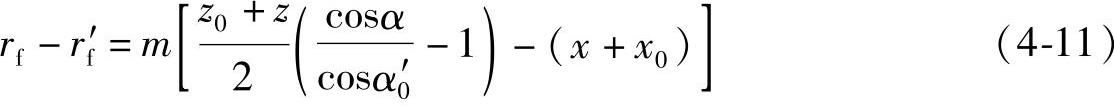
根据上式，当（x+x₀）=0时，则加出的齿轮，其齿根圆半径与计算的值相等，即齿轮的顶隙为标准值0.25m；若（x+x₀）>0或（x+x₀）<0时，加工出的齿轮的根圆都将减小，即齿轮顶隙都比标准值0.25m要大。当其他条件不变，（x+x₀）的绝对值大时，则齿根圆半径减小值也大；其他条件不变，当插齿刀的齿数越少时，齿轮的齿根圆半径减少得越多。因此，当被加工齿轮的顶隙有严格要求时，则要限制插齿刀的齿顶高，或控制插齿刀的最大及最小变位系数x_0max、x_0min，同时避免采用齿数少的插齿刀。

插齿刀本身可看作一个变位齿轮，随着刀具前刃面的不断磨损，插齿刀的顶圆直径d_a0、分度圆弧齿厚s₀、变位系数x₀都相应发生变化。当x₀>0时，加工齿轮时相当于一个正变位齿轮与另一齿轮相啮合；当插齿刀刃磨到原始截面时，即x₀=0时，相当于一个标准齿轮与另一齿轮相啮合；当x₀<0时，相当于一个负变位齿轮与另一齿轮相啮合。因此，对于不同磨损程度的插齿刀在加工齿轮时，均应按无侧隙来进行啮合。

在实际加工时，并不需要进行上述计算，而只要求达到所需的齿厚便可。齿厚的保证是通过实际测量来得到的，即切第一刀后，先测一次公法线长度，根据测得的值与所需值之差再进刀，直至加工出所需齿厚的齿轮。