计算2.4渐开线齿形

我们已讨论了渐开线一些性质，但在制造和测量渐开线齿轮时，往往需要知道渐开线齿形的各点坐标值，下面叙述一下渐开线齿形的坐标计算方法。

1.渐开线的极坐标计算法

从图2-12可知，渐开线上任意一点K_x的位置可用极坐标（r_x、θ_x）表示，r_x为任意点的向量半径，θ_x为任意点的渐开角。可直接利用渐开线方程求得

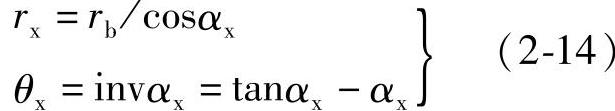
式中 α_x——渐开线上任意点K_x上的压力角；

r_b——基圆半径，r_b=rcosα。

若已知基圆半径r_b，在每取一个α_x值时，就可算渐开线上各相应点的极坐标（r_x，θ_x）。当算出若干点后，就可以在坐标纸上绘出整条渐开线。

图2-12 用极坐标法计算渐开线齿形

【例2-1】 已知齿轮m=2.5，z=30，α=20°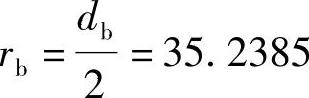，，计算渐开线齿形。

解 1）设α_x=28°时，则渐开线上该点的极坐标为

2）设α_x=20°时，则渐开线在分度圆上的极坐标为

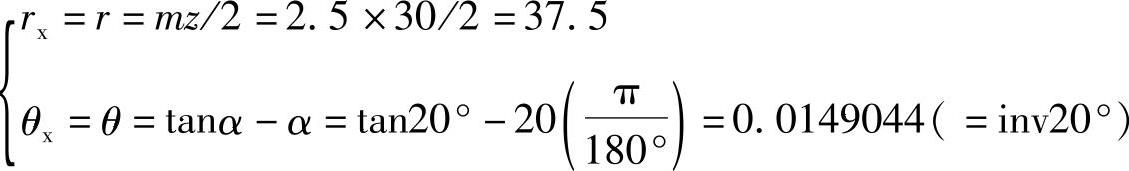
2.渐开线的直角坐标计算法

当用盘形或指形铣刀加工齿轮时，刀具的齿形应做成齿轮齿槽形状，即对称的渐开线齿形，如图2-13所示。为了加工和测量方便，常把渐开线齿形上各点用直角坐标表示。这就需要列出渐开线的直角坐标方程来进行计算。在图2-13中，齿轮的轴心为O′，齿槽的对称线为y轴，齿根圆与y轴的交点O为坐标系的原点。从图中可列出渐开线任意点K_x的直角坐标方程为

式中 δ_x=δ+（θ_x-θ）。

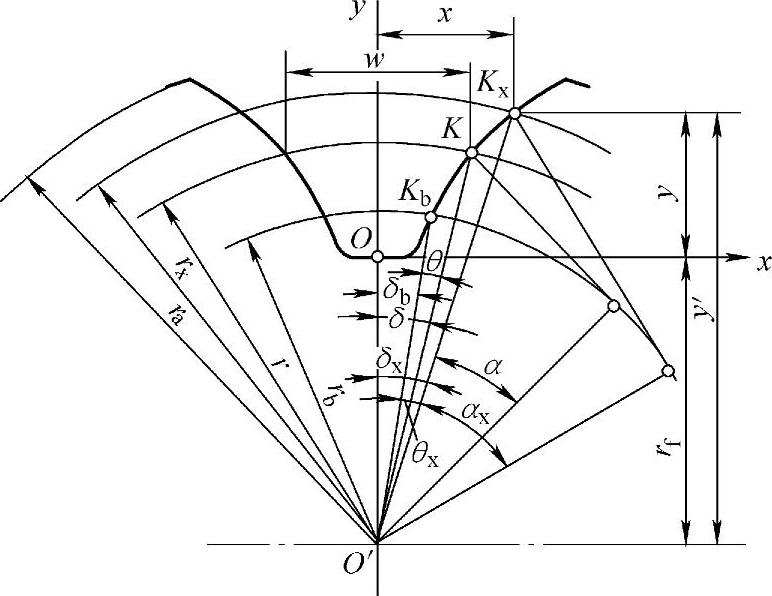
图2-13 用直角坐标法计算齿形

1），对于标准直齿轮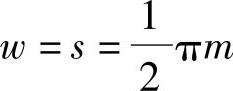，d=mz。(www.xing528.com)

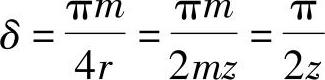
2）θ_x=invαx

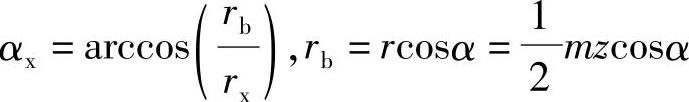
3）θ=invα，对于标准齿轮α=20°。

从直角坐标式（2-15）可知，当一个齿轮的模数m、齿数z和分度圆压力角α已知时，就可算出基圆半径r_b和齿根圆半径r_f。如果给出一系列向量半径r_x，就能算出渐开线上各点的直角坐标，以及绘出齿槽的形状，也就可绘出刀具的齿形图。

3.用圆弧代替渐开线齿形法

当齿轮精度要求不高时，可采用近似法，即用圆弧来代替渐开线齿形。用这种方法，不仅可使计算简化，还能使铲磨铣刀齿形时修整砂轮变容易，便于制造磨齿形的齿形铣刀。

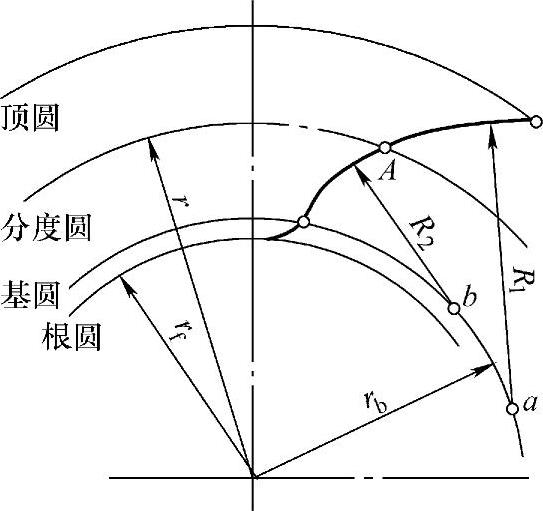
图2-14 圆弧近似渐开线齿形法

当齿轮齿数z<55时，铣刀齿形需用两段圆弧，半径为R₁、R₂来代替，如图2-14所示，这两个圆弧的圆心均应在基圆上。

当齿轮齿数较多时，如z>55，则整个齿形曲率差较小，可用一个圆弧R₁来代替。

当α=20°时，可用下式计算

式中

表2-4是根据式（2-17）和式（2-18）求出的系数ρ′和ρ″的数值。

表2-4 α=20°时ρ′和ρ″值