渐开线齿轮传动的标准设计

在工程中，齿轮总是成对使用的，因此，还要进一步研究齿轮啮合传动时的情况。

1.一对渐开线齿轮的正确啮合条件

前面我们已论及，渐开线齿轮的一对齿廓在啮合时，可保证传动比固定不变。因此，齿轮不能只靠一对轮齿啮合传动，而是靠多对齿依次啮合来传动的。于是，如何保证齿轮的轮齿在交替啮合时，仍能使传动比为常数，这是保证齿轮整个传动过程中传动比固定不变的关键。

一对渐开线齿廓在任何位置啮合时，啮合点均应在基圆的内公切线N₁N₂上，即直线N₁N₂为啮合线。如图2-9所示，当齿轮1主动时，齿根首先推动从动齿轮2的齿顶在啮合线上啮合，于是，齿轮2的齿顶圆与啮合线的交点B₂，即为起始啮合点。随着啮合传动的继续进行，当主动轮1转到齿顶圆与啮合线N₁N₂的交点B₁时，该对轮齿便脱离啮合，即B₁点为啮合的终止点。这样，一对齿轮的轮齿实际只能在啮合线N₁N₂上的B₁B₂段进行，故B₁B₂称为实际啮合线。随着齿轮齿数的不断增多，即齿顶圆增大，B₁、B₂点将分别向N₂、N₁点移近，但是，由于基圆以内没有渐开线，所以实际啮合点不会超过N₁、N₂点，故N₁、N2点称为极限啮合点，线段N₁N₂称为理论啮合线。

从以上啮合过程分析中可以看出，为保证轮齿交替啮合时齿轮的传动比仍为常数，必须要求：前一对轮齿在K点啮合，尚未到达啮合终止点B₁时，后一对轮齿就在B₂点开始啮合，如图2-9所示。亦即前一对轮齿脱离啮合时，后一对轮齿已进入正常啮合，这样才能使前后两对轮齿交替啮合过程中，不致产生冲击，保证传动比为常数。

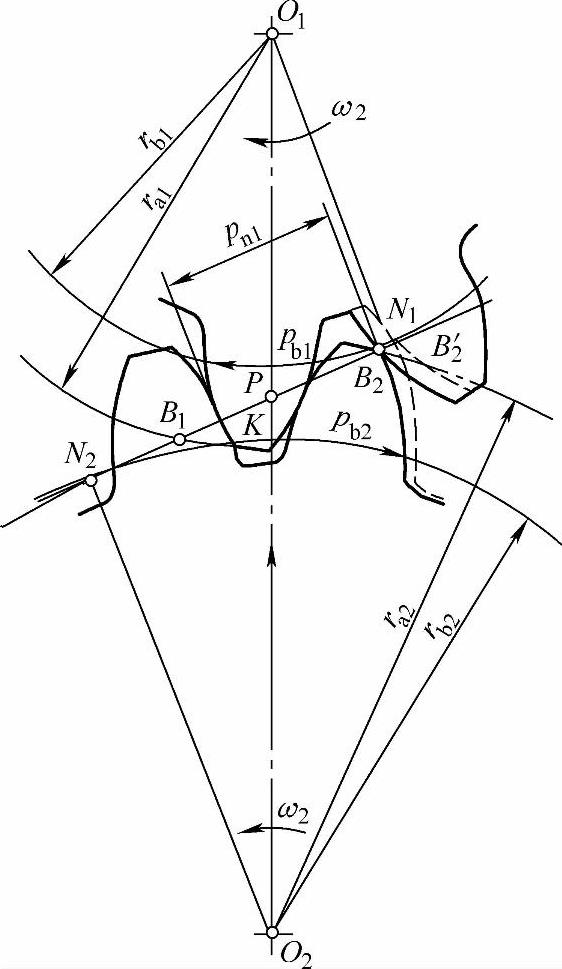
图2-9 渐开线齿轮正确啮合

从图2-9中可以看出，前一对轮齿的啮合点K到后一对轮齿的啮合点B₂之间的距离B₂K，既是齿轮1的法向齿距p_n1相邻两齿同一侧齿廓间法线方向的距离，又是齿轮2的法向齿距p_n2。可见，为保证前后两对轮齿同时在K点和B₂点啮合，则

p_n1=p_n2

否则，若p_n1>p_n2，当前面一对轮齿在K点啮合，齿轮2的后一个轮齿到达B₂点时，齿轮1的后一个轮齿必然处于图中的虚线位置，即p_n1=B₂′K>p_n2=B₂K。这样，两齿轮的后一对轮齿间就存在间隙，致使前一对轮齿转至啮出点B₁而不能脱离接触，这时齿轮1的齿顶棱推动齿轮2作减速运动，直至后一对轮齿开始啮合。在这一段时间内，就不能保证传动比为常数。反之，若p_n1<p_n2，则齿轮的后一轮齿将处于图中虚线位置，而产生楔紧现象，使传动不能正常进行。因此，只有p_n1=p_n2才能保证轮齿交替啮合时，既无冲击又不会产生楔紧现象，从而保证齿轮的全部轮齿啮合过程的传动比为常数。

根据渐开线的性质，齿轮1的法向齿距p_n1等于基圆齿距p_b1，即p_n1=p_b1；齿轮2的法向齿距p_n2等于基圆齿距p_b2。于是，保证一对齿轮的传动比为常数的正确啮合条件应为两齿轮的基圆齿距相等，即

p_b1=p_b2 （2-9）

由于基圆周长为

p_bz=πd_b=πmzcosα

因此基圆齿距p_b应为

p_b=πmcosα （2-10）

所以齿轮1和齿轮2的基圆齿距p_b1和p_b2应分别为

p_b1=πm₁cosα₁

p_b2=πm₂cosα₂

将p_b1和p_b2之值代入式（2-9）得(www.xing528.com)

m₁cosα₁=m₂cosα₂ （2-11）

这就是两个齿轮的正确啮合条件。式中m₁、m₂，α₁、α₂分别为两齿轮的模数和压力角。如果两齿轮的模数m₁、m₂和分度圆压力角α₁、α₂可以任意选取时，只要式（2-9）成立，这一对齿轮就可以正确啮合。在生产中，为了提高加工的工艺性，可以应用小压力角滚刀，如α=15°来加工大压力角如α=20°的渐开线齿轮，此时滚刀的模数与被加工齿轮的模数就不应相等。也可以用0°的平面砂轮来磨削α=20°的渐开线齿轮。

但是，模数m和压力角α均已标准化，不能任意选取，所以要满足式（2-9），一般只有要求：

于是便得结论：一对渐开线齿轮的正确啮合条件是，两齿轮的模数相等，分度圆的压力角相等。这也是渐开线齿轮的互换性条件。

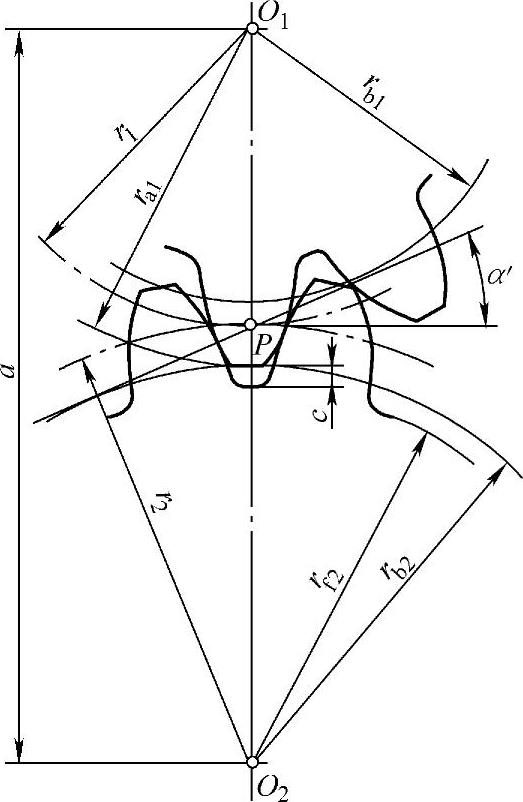
图2-10 外啮合直齿轮传动

2.渐开线标准齿轮传动的中心距a及啮合角α′

（1）外啮合传动 一对齿轮在啮合传动过程中，为保证运行和润滑良好，一齿轮的齿顶与另一齿轮的齿根之间必须留有一定的顶隙，顶隙c规定为标准值，即c=c^*m，其中c^*为顶隙系数，通常c^*=0.25。图2-10所示为一对外啮合渐开线标准齿轮的啮合传动。为保证无侧隙啮合，两齿轮的分度圆应为相切的相互纯滚动的节圆，即一齿轮的分度圆齿厚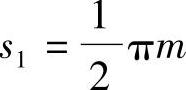，应等于另一齿轮的齿槽宽

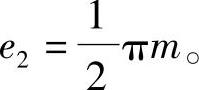
因此，一对渐开线标准齿轮外啮合传动时，其中心距a应等于两齿轮分度圆半径之和，即

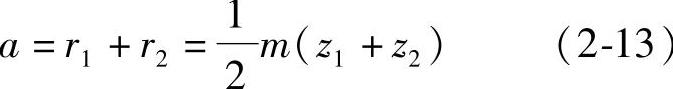
啮合角是齿轮传动的节圆压力角，即是啮合节点P的速度矢量与啮合线—齿面作用力的方向所夹的锐角，用α′表示。由于渐开线标准齿轮啮合时，两分度圆相切，即节圆与分度圆重合，故啮合角α′就等于分度圆压力角，即α′=α。

若由于齿轮的制造及安装误差，或由于工作时的径向力而引起轴的变形等原因，而使两齿轮的实际中心距a′大于设计的标准中心距a时，两齿轮的分度圆就不再相切，节圆与分度圆不再重合了，此时两节圆半径大于各自的分度圆半径，因而啮合角α′大于分度圆压力角α。

（2）齿轮齿条啮合传动 图2-11a表示齿轮与齿条标准安装啮合时的情况，即齿轮分度圆与齿条的分度线相切。此时，齿轮的啮合节圆与分度圆重合，齿条的节线与分度线重合，因此，传动的啮合角α′等于齿轮的分度圆压力角α，α即是齿条的齿形角。

在一对齿轮啮合传动中，啮合线N₁N₂为两齿轮基圆的内公切线，而齿轮与齿条啮合传动中，啮合线应与齿轮1的基圆切于N₁点，而与齿条2的“基圆”的切点N₂应在无穷远处，因而其啮合线可以这样求得：作一直线与齿轮1的基圆相切，并与齿条的一侧齿廓相垂直，该直线即为齿轮齿条传动的啮合线，与齿条分度线的夹角即为啮合角α′，如图2-11a所示。

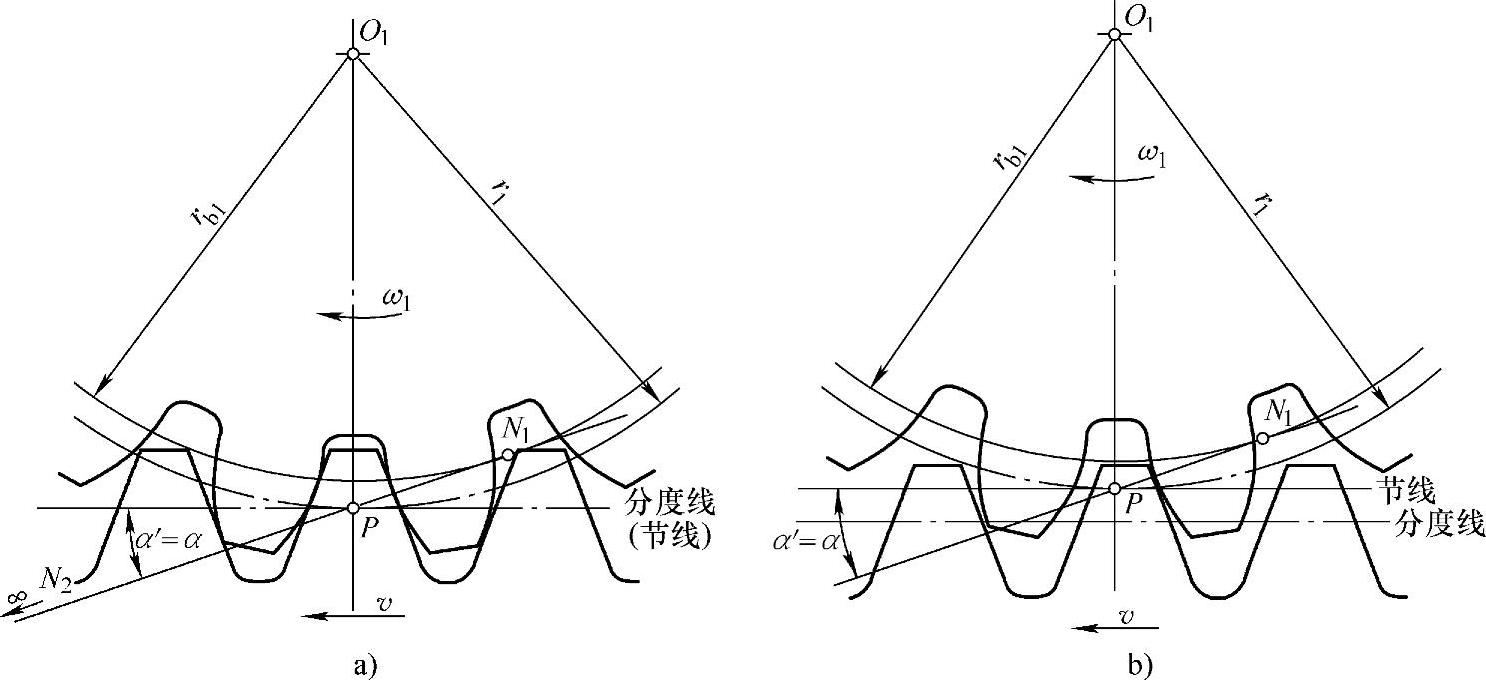
图2-11 齿轮齿条的啮合传动

当齿条相对于齿轮移近或移远，即相当于改变中心时，由于啮合线既要切于齿轮的基圆，又要垂直于齿条的齿廓，又由于齿条外移后的齿廓与未移前的齿廓是平行的，因而齿条外移后，啮合线的位置并不会改变，如图2-11b所示，啮合角α′也不会改变。所以齿轮与齿条啮合传动时，不论是否为标准安装，齿轮的节圆恒与分度圆相重合，而齿条的节线与分度线则不一定重合。当标准安装时，齿条的节线与分度线重合，如图2-11a所示。当非标准安装时，齿条的节线与分度线不重合，如图2-11b为齿条外移时的情况，此时，齿条节线与齿轮分度圆切点，即啮合节点P的位置总是不变的。因此，不论是否为标准安装，齿轮与齿条啮合传动时的啮合角α′恒等齿条的齿形角α。