消光系数的物理意义探究

线性消光系数σe的物理意义是光强衰减到原来的约0.36时的介质厚度。

质量消光系数αe的物理意义是光强衰减到原来的约0.36时每克烟幕的截面积。αe与粒子的种类、粒径大小分布、粒子的形状及取向、粒子的表面性质（粗糙度）、光的波长等因素有关。当烟幕体系确定时，αe只与光的波长有关。因此，通常用质量消光系数（又称消光截面）表示烟幕的消光特性。

线性消光系数指在恒定的烟幕浓度下，透过率对数与光程直线关系的比例因子；而质量消光系数是指透过率对数与光程浓度乘积直线关系的比例因子。

对于单个球形粒子：

式中，G——粒子的几何截面积；

V——粒子的体积。

对于粒数浓度为N的单分散烟幕：

式中，AP——粒子的截面，假设它为球形，以d表示其直径。

对于多分散烟幕：

式中，Qe——米散射因子（几何截面除以电磁消光截面）；

ρ——质量密度；

m——复反射指数；

r——烟幕粒子的半径；

λ——波长；

N（r）——粒径的粒数分布密度函数。

由于m和N（r）均未知，αe通常用试验的方法获得。由方程式（9.39）可知，如果尺寸分布改变，αe也随即改变。任何像凝聚、沉降那样的动力过程，或者以不同的尺寸分布产生新的烟幕，都将改变N（r）。像磷和HC那样的吸水性烟幕，其尺寸分布取决于相对湿度，因而αe是相对湿度的函数。

对于浓密的烟幕，可能发生复散射，二级前向散射在理论上已做了处理。结果表明，对于典型的自然发生的烟幕，为了获得真实的消光值，可以将校正因子R用于测得的透射率。该因子是检测器（FOV）、粒径分布及反射指数的函数，在比尔定律中：

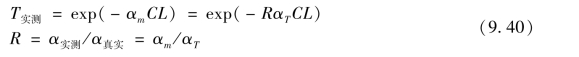
式中，αT——满足朗伯-比尔定律条件下测定的消光系数；

αm——不满足朗伯-比尔定律条件下（高浓度）测定的消光系数。

当一束光通过气溶胶时，会发生衰减。气溶胶对光的这一作用性质正是烟幕能够起到遮蔽效应的主要原因。烟幕消光的基本原理如图9.1所示。烟幕消光是烟幕气溶胶微粒对入射辐射的吸收和散射衰减的综合结果。

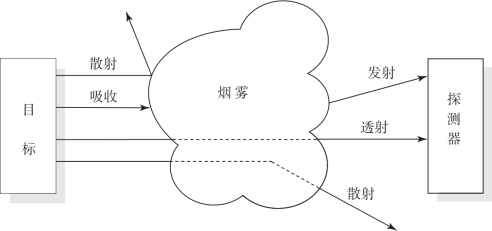
图9.1　烟幕的消光机理

9.2.2.1　吸收衰减消光机理

烟幕吸收衰减消光，是烟幕气溶胶微粒将入射光的能量转化成其他形式的内能（如热能等）的结果。量子理论表明，气溶胶微粒分子的运动能量是量子化的。分子运动能量包括分子整体的转动能量Er、各原子在平衡位置上的振动能量Eυ和原子中电子相对于原子核的运动能量Ee。分子的每一运动状态都具有一定的能量，或者说属于一定的能级。当光（即电磁辐射）与气溶胶微粒分子相互作用时，如果其能量（E=hυ）与分子的Er、Eυ或Ee的能级的能量差值相当，则分子产生相应的能级跃迁，分子就吸收或发射一定频率的电磁辐射。这种由于入射辐射引起气溶胶微粒分子能量的转变，只有在玻尔频率条件满足式（9.41）条件时才能发生，并且当分子从低能态被激发到高能态时，它表现为吸收；从高能态跳回到低能态时，呈现出辐射。

因此，光在烟幕中传输的吸收衰减过程，是光与烟幕微粒分子相互作用，使分子能级从低能态跃迁到高能态而表现出的吸收作用。这种吸收具有选择性，其光谱是不连续的。不同分子吸收的波长和吸收能力也是不相同的。吸收衰减消光在本质上是分子的内能状态发生了变化。

从电子论的观点看，光在气溶胶中传输时被吸收，是由于光波的电矢量使气溶胶微粒结构中做谐振的原子和分子获得能量而做受迫振动，当受迫振动的原子或分子与其他原子或分子发生碰撞时，振动能量即转变成平动动能，此时分子热运动加剧，即该部分光能被转化成热能而消失。

光被气溶胶吸收的衰减系数可由式（9.36）朗伯-比尔定律求得：

式中，I0（λ）——进入气溶胶中的光的强度，cd；

I（λ）——从气溶胶内射出的光的强度，cd；

αe（λ）——气溶胶的消光系数；

c——气溶胶的质量浓度，g·m-3；

L——气溶胶的吸收层厚度，m。

9.2.2.2　散射衰减消光机理

烟幕散射衰减消光，是烟幕气溶胶微粒截获入射辐射能量形成次生波后，再向四周辐射而使入射光在原传播方向上能量减少的一个过程。

光作为一种电磁波，当进入烟幕中时，入射辐射能量一部分将被烟幕气溶胶微粒截获。微粒截获能量后即构成次生（二次）的波源，产生次生电磁波，再向外辐射出去，这就使得入射辐射在原传播方向上的能量降低。假设烟幕气溶胶微粒是一个均质微球，它对入射光的散射衰减如图9.2所示。

图9.2　均质微球对光的散射

从微观的角度来说，次生电磁波的产生是截获能量后的微粒内原子、分子被入射辐射电磁场诱导极化形成偶极子，该偶极子随入射电磁振荡而做同一频率的受迫振动，构成了次生波源，产生出次生波。由多个原子、分子构成的微粒内总存在着很多这样振动的偶极子，它们所产生出的次生波不仅频率与入射光一致，而且彼此之间也存在固定相位，会形成相干光。但因为气溶胶是非均质体系，微粒数密度（或浓度）因布朗运动而改变，故次生波的相干性被破坏，因此多个振动的偶极子所产生的次生波会在微粒周围叠加，随后向其周围空间散布开，这样就产生了散射作用。

必须指出的是，次生波是微粒内原子、分子因偶极化与辐射电磁场作用下才产生出的，光只是通过次生波的产生和辐射使其在原传播方向上能量减少，而入射辐射总能量并未发生变化，这与吸收衰减发生内能状态变化在本质上是不同的。

9.2.2.3　气溶胶对光散射的影响因素

气溶胶对光散射的主要影响因素有粒径、粒子形状和取向、粒子的表面性质（粗糙度）、粒子的折射率、粒子的均匀性等。

（1）粒径。气溶胶微粒粒径不同，光散射将呈现出不同的特性。当微粒半径r远小于入射光波长λ时，呈现出分子散射特性；当微粒半径r大于入射光波长λ时，呈现出无选择性散射特点。为了描述粒径对光散射性质的影响，定义了无因次的粒径参数χ=2πr/λ，它是微粒半径r和入射光波长λ的函数。对于球形粒子来说，显然χ是粒子的周长与波长之比。

（2）粒子形状和取向。不同形状的粒子，以及它们相对于入射光和观测方向的取向不同，都影响着光的散射。目前对球形、圆柱形、圆盘形及椭球形粒子的消光计算已经建立起了模型，但对其他形状粒子的消光尚不能进行理论计算。

（3）粒子的表面性质（粗糙度）。粒子表面是光滑的还是粗糙的，将影响着光的散射性能。粒子表面若为光滑的镜面，则表现为镜面反射；若为粗糙的表面，则呈现漫反射。

（4）粒子的折射率。光在气溶胶中的传播与气溶胶微粒的折射率m=n-ik有关。折射率的实部n和虚部k的大小直接影响消光性能。

（5）粒子的均匀性。大多数气溶胶的粒子是不均匀的，它们都是一些混合粒子。鉴于这些粒子会凝并形成聚合体，使混合粒子各部分的密度出现很大差异，因粒子各部分的折射率不同，从而影响光散射的性能。

9.2.2.4　瑞利散射和米氏散射

光的散射有线性和非线性散射之分。线性散射时，光的频率等于入射光的频率，散射时没有新频率的光产生。非线性散射的特点是，在散射光中，除了入射光的频率或谱线外，还有新频率的光或新谱线产生。瑞利散射（Rayleigh Scattering）和米氏散射（Mie Scattering）属于线性散射，拉曼散射（Raman Scattering）和布里渊散射（Brillouin Scattering）则属于非线性散射。气溶胶对光散射的研究涉及更多的是线性的瑞利散射和米氏散射，现分别介绍如下。

（1）瑞利散射。瑞利散射是讨论粒子半径r远小于入射光波长λ的散射理论问题。它是由英国物理学家J.瑞利（John Rayleigh）于1871年创立的。瑞利认为，在大气中比入射辐射波长小得多的粒子，其对入射辐射的散射与分子散射的方式完全相同，并推导出了相应的瑞利散射公式。当散射粒子波长在（1/5～1/10）λ以下时，瑞利散射有如下三个特点：

①散射光的强度随观察方向与入射光方向之间的夹角θ而变。当入射光是自然光时，散射光强Iθ和θ之间的关系为：(www.xing528.com)

式中，Iπ/2——垂直于入射光方向上（即θ=π/2时）散射光的强度。瑞利散射光强的空间分布图如图9.3所示。由于散射光强分布相对于原光束的传播方向是对称的，瑞利散射光强的空间分布曲面是以原入射光束的传播方向为轴的旋转曲面。

图9.3　瑞利散射光强分布图

②散射光是偏振光。不论入射光是自然光还是偏振光均如此，并且偏振度P与观察方向θ有关。对于各向同性介质，偏振度P为：

散射光偏振是因为光波是横波。

③散射光的光强与入射光的波长λ的四次方成反比，即：

由式（9.44）可知，波长越短的光，其散射越强烈。由此可以解释天空的蓝色和落日红色余晖。这是因为天空中分子对短波长蓝色光的散射比对其他颜色光散射强烈得多，因此看到晴朗天空的颜色是蔚蓝色的；而在日落西山时，光穿过大气层厚度较中午时阳光穿过的厚度大得多，故被散射掉的短波比长波要多，所以看落日时呈红色余晖。

对于球形粒子的气溶胶，瑞利散射光强计算通常采用下式：

式中，I——散射光的强度；

I0——非偏振的入射光强度；

R——观察距粒子中心的距离；

N——粒子数目；

V——粒子体积；

m——折射率。

瑞利散射系数的计算公式为：

式中，N′——单位体积内的粒子数。

瑞利散射因粒径比波长小得多，其散射性质与粒子形状无关。如果粒子的折射率近似为1，瑞利散射理论可以推广到更大的粒子，这就是瑞利-甘斯散射。在瑞利-甘斯散射区，散射与粒子的形状有关，当粒子几何形状较简单时，可对粒子形状导出有关的校正项，如果粒子比波长大得多，则利用几何光学计算各种非球形粒子的反射光和折射光。

（2）米氏散射

米氏散射是讨论粒子半径与光波波长同量级（或更大）的散射理论问题。它是由德国物理学家G.米（Gustar Mie）于1908年提出的。米氏论述了由任意大小和折射率均匀的球形粒子产生的光散射问题，并给出了具有适当边界条件的麦克斯韦方程的解。

米氏散射适用于有相同直径和成分的、无规则分布且彼此分开的距离比一个波长大得多的微粒对光的散射情况。在该情况下，不同微粒散射光之间没有相干的相位关系，因而总散射能量就等于被一个球散射的能量与球总数的乘积。此外，对于吸收和非吸收的球体，以及其粒径从分子大小直至用几何光学处理的足够大的颗粒，该理论都是有效的。当粒径在瑞利散射范围内时，该理论与瑞利理论相同。

米氏散射将散射粒子看作是导电小球，它们在光波电场中发生极化而向外辐射电磁波。米氏散射的特点是散射光强不是与波长λ的四次方成反比，而是和λ的较低次幂成反比。因此，散射光强与光波波长关系不如瑞利散射那样密切，散射光呈白色而不是蓝色。另外，虽然散射光仍为偏振光，但偏振度随ω/λ的增加而减小（ω是米氏散射粒子的线度或直径）。再有，散射光强度的角分布也随ω/λ而变，和瑞利散射相比，其前向散射加强，后向散射减弱，如图9.4所示。

图9.4　米氏散射光强分布

当入射光是非偏振的自然光时，米氏散射光强度有如下形式的空间分布：

式中，Iλ——散射光的强度（单位时间内单位面积上的能量）；

I0，λ——入射光的强度（单位时间内单位面积上的能量）；

i1——散射光的强度函数（表示垂直的偏振分量）；

i2——散射光的强度函数（表示平行的偏振分量）；

k=2π/λ；χ=2πr/λ——无因次粒径参数；

R——距散射粒子中心的距离；

m——粒子相对于周围介质的折射率；

θ——入射光与散射光之间的夹角（θ=0°时，定义为前向散射）。

i1和i2相应地与电矢量在垂直于和平行于观测平面上的分量的平方成正比（观测平面是入射光与被测的散射光所构成的平面），其数学表达式均为无穷级数：

式中，an、bn——振幅函数，均属复数，与χ和m相关，但与散射角θ无关，其物理意义是由二极矩、四极矩等开始的第n电极矩（an）和磁极矩（bn）；

πn、τn——只是散射角θ的函数，包含次数n和变量cosθ的勒让德（Legendre）多项式的一阶与二阶导数。

在米氏散射中，粒子的散射截面积σs定义为：

式中，Is——总散射光，它等于在σs上的总入射光I。用与之相仿的定义给出粒子的吸收截面σa和消光截面σe，于是：

散射截面与几何截面G之比称为散射效率因子Qs，即ρs/G=Qs。吸收效率因子Qa和消光效率因子Qe按类似方法定义给出。

散射效率因子可以通过对dΩ（dΩ=2πsinθdθ）积分得到：

也可以直接从振幅函数an和bn导出：

消光效率因子Qe也可以直接由振幅函数导出：

式中，Rd表示取复数的实部。由于吸收和散射两个消光过程的消光效应是可加和的，所以：