气溶胶动力学探究

9.1.2.1　气溶胶粒子沉降

气溶胶粒子的沉降过程，是粒子在外力作用下和介质分离的过程。除重力沉降外，气溶胶粒子的沉降还包括离心机的分离、电场中的沉降及化学工程中的反过程——流化床等。极端稀释体系沉降问题早在1851年就由斯托克斯（Stokes）用孤粒子沉降理论解决了，这就是著名的斯托克斯介质对球形粒子运动的阻力公式：

式中，FD——介质对球形粒子运动的阻力；

η——空气的黏性系数；

r——气溶胶微粒半径；

v——气溶胶微粒运动速度。

对于一个仅在重力作用下以末速度下降的球体而言，阻力F就等于球的重力减去流体的举力，即

式中，g——重力加速度；

ρ——微粒密度；

ρ′——介质密度；

r——微粒半径。

根据式（9.1）和式（9.2），可以得到有关重力末速度的方程式：

将之变换得到用于烟幕微粒沉降的速度计算公式：

由于空气ρ′很小，可以忽略不计，则

令，则烟幕微粒沉降的速度计算公式变换为：

微粒在时间t内，由于重力的作用，下降路程为：

非极端稀释多粒子的气溶胶沉降问题要比孤粒子沉降复杂得多，通常将它们分为两类来讨论：一类是在无界空间中气溶胶云的沉降，其速度将大于孤粒子重力末速度，这类沉降称为“增速沉降”；另一类是在有界空间中（例如在烟幕箱或沉淀池中）粒子的沉降，它一般小于孤粒子重力末速度，这类沉降称为“阻滞沉降”。在多粒子共存条件下，某一粒子的沉降速度与其他粒子空间构形有关，空间构形不同，则该粒子沉降速度不同，粒子构形又是一个多维随机场，因而该粒子沉降速度应是一随机矢量。由于所讨论的粒子被看作球形的且是刚性均匀地分布在静止的容器中，粒子在重力作用下沉降速度取决于粒子的大小、密度与介质密度之差，以及粒子的体积浓度等。但粒子的体积浓度必将反映出粒子间的流体动力相互作用问题。随着粒子沉降速度加快或粒子尺寸的变大，流体的黏性、惯性影响也变得突出，这就需要考虑到沉降速度与雷诺（Reynolds）数的关系问题，则有：

式中，vt——粒子末速度；

η——流体黏性系数；

Re——粒子雷诺数；

ρ′——气体介质密度；

d——球形粒子直径。

又因为

式中，CD——球形粒子阻力系数。

根据式（9.9）的等号右边项计算值，从气溶胶手册上查得阻力系数随雷诺数变化值，即可获得Re值，再将Re代入式（9.8），即可求得粒子速度vt。

当气溶胶粒子的大小接近气体分子的平均自由程时，粒子的迁移率增加，颗粒表面上有“滑动”。因此，当粒子直径小于1μm时，必须用滑动修正系数即坎宁汉（Cunighan）系数Cc来修正式（9.8），则粒子速度为：

滑动系数Cc最早的表达式为：

式中，λ——分子平均自由程；

A——近似于1的系数。

弗拉纳根（Flanagan）和泰勒（Taylor）进一步改进式（9.11），把滑动修正系数推广到比分子平均自由程更小的粒子上去，则：

式中，A、Q、b——常数。

按分子平均自由程为9.332×10-6 cm来计算时，取值为A=1.234，Q=0.413，b=0.904。

9.1.2.2　气溶胶粒子的碰并

将一个障碍物放入流动的气溶胶中时，较小的粒子能绕过障碍物跟着气体流走，而较大的粒子由于具有较大的惯性，不能随着气体改变方向，于是被障碍物截获，这一现象就是碰并。气溶胶体系中一个粒子与另一个粒子的碰并过程（包括上述粒子与障碍物之间的碰并捕获过程），实质上是粒子从体系中消失的过程。当气溶胶体系中存在着碰并现象时，其数密度将不断减小，而粒子平均大小与平均沉降速度则不断增加。因此，粒子从介质中分离出来的速度也加快。所以，通常把存在着碰并现象的体系叫不稳定体系；反之，则叫稳定体系。

气溶胶粒子的碰并现象实际上包括了以下两个过程：

（1）碰撞过程：两个或两个以上的粒子，在外力（重力、离心力、外流场作用力等）或来自介质的布朗热动力作用下而产生了相对运动，此时粒子相互接近以致发生接触碰撞。

（2）并合过程：两个或两个以上的粒子碰撞后，由于粒子表面的各种物理的、化学的作用，粒子发生并合，其中也包括粒子碰撞后不能并合又反弹回去的过程。碰并现象对气溶胶粒子的收集和测量具有实际意义。碰并率即碰并效率，可用碰并参数Pin来表达。球形粒子碰撞在横放于气溶胶流体中的孤立圆柱体、球体、平板或圆盘上的Pin值用下式表示：

式中，d0——圆柱体、球体、圆盘的直径或平板宽度；

v——球形粒子速度。

9.1.2.3　气溶胶粒子的布朗（Brown）运动和扩散

气溶胶粒子在气体中的扩散是布朗运动的结果。小于1μm的粒子才产生布朗运动。布朗运动是1827年英国植物学家布朗在研究花粉时发现的。布朗运动是气体介质的分子和气溶胶微粒撞击的结果。布朗运动是无规则的。就单个粒子而言，它们向各方向运动的概率是均等的。但在粒子浓度较高的区域，由于单位体积内粒子数较周围的多，出现“出多进少”的现象，造成区域内浓度降低；而低浓度区域则相反，这就表现为扩散。扩散是布朗运动的宏观表现。由布朗运动引起粒子的位移，对于大多数气溶胶粒子而言占有重要地位。例如粒子半径为0.001～0.01μm时，1 s内由布朗运动引起的位移约为10μm，比重力沉降位移大两个量级；粒子半径为0.1～1.0μm时，其位移量级也在1～10μm，仍可与重力位移相比。所以，气溶胶的扩散与沉降具有同等重要性。

爱因斯坦（Einstein）通过对布朗运动的研究，给出了粒子平均位移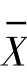与粒子半径r、介质黏度η、温度T及位移时间t之间的关系式：

式中，NA——阿伏伽德罗常数。

通常只考虑小于1μm粒子的气溶胶的扩散问题，并用扩散系数DB（cm2/s）来表征扩散效果。DB值越大，说明布朗运动越剧烈，扩散越快。其计算式如下：

式中，k——玻尔兹曼常数；

B——迁移率，(https://www.xing528.com)

T——绝对温度。

实际应用中的气溶胶扩散有两种情况：一是粒子在静止空气中的扩散沉积；二是在流体系统（主要是层流）中的扩散。在静止气体中，当扩散是在两个垂直平行壁间进行时，气溶胶粒子浓度减小，按下式进行计算：

式中，n0——粒子初始浓度；

n——粒子在时间t时的浓度；

DB——扩散系数；

Q——整数；

t——时间；

h——两壁间距离。

当扩散在半径为R′的球形容器内进行时，气溶胶粒子浓度减小，按下式计算：

在层流中，对于间距为2h的平行板通道内粒子浓度的减小，按下式计算：

式中，，其中L为通道长度，v-为通道中气体的平均流速。

9.1.2.4　气溶胶粒子的凝并

气溶胶粒子在大气中运动时相互接触（碰撞）而形成较大粒子的过程叫凝并（凝聚、凝结）。凝并的接触（碰撞）过程有热力的、电力的、磁力的、流体力学的、分子的、重力的、惯性力的、声的等。对烟幕（气溶胶）凝并的研究，需要考虑热力凝并、荷电粒子凝并、湍流凝并和动力凝并等。

（1）热力凝并。气溶胶粒子因布朗运动，彼此间发生频繁的碰撞（碰撞频率与粒子浓度有关），即产生热力凝并。布朗运动两粒子相碰就会黏附在一起，形成一个聚合粒子。对于球形粒子的气溶胶，粒子浓度因热力凝并作用而减小的数学描述如下：

式中，为凝并系数；

k——玻尔兹曼常数；

T——绝对温度；

η——流体黏性系数；

S——粒子作用范围与粒子半径之比（对于有效碰撞，S=2）；

Cc——滑动修正系数。

积分上式，则有：

式中，n0——时间t=0时的粒子数。

（2）荷电粒子的凝并。粒子带有电荷时，就有可能增强或者减弱粒子的凝并。这要看电荷是异性的（相吸）还是同性的（相斥）。带电粒子与非带电粒子的凝并常数之比为：

式中，x=2rh；

r——粒子半径；

h——粒子间距离；

φ——粒子间的电势。

（3）湍流凝并。气溶胶粒子处于湍流中，其凝并会由于流体的混乱运动而增强。湍流凝并常数与热力凝并常数之比KT为：

式中，a=25（对于交换过程的湍流）或a=4（对于梯度凝并的湍流）；

ε——每克每秒所耗散的能量。

（4）动力凝并。受外场力（重力、外加电场力等）作用引起的粒子凝并过程称为动力凝并。粒子大小不同，其运动速度也不同，往往是大粒子捕获住小粒子。粒子的捕获速率v由下式给出：

式中，β——捕获效率（即收集效率）；

r1——大粒子的半径；

vs——大粒子极限沉降速度。

在大小两种粒子都带荷电的情况下，捕获效率由下式给出：

式中，q1——大粒子的电荷；

q2——小粒子的电荷；

ρ——粒子密度（假定大小粒子密度相同）；

r2——小粒子的半径；

g——重力加速度。

（5）气溶胶粒子沉降、扩散和凝并的综合作用。凝并、扩散和沉降的综合作用将引起气溶胶的粒子浓度减小。在一个密闭容器内，所观测到的粒子浓度减小的原因是：

①粒子因沉降而沉积于容器底部；

②粒子在容器四壁和底部的扩散沉积；

③粒子发生凝并。

气溶胶粒子沉降、扩散和凝并三者的作用各不相同。沉降和扩散一般不能同时起作用，这是因为只有当粒子小于1μm时，扩散才发生，而此时的沉降作用微不足道；相反，沉降速率可观时，粒子扩散迁移率极小，扩散作用可以忽略不计。无论是沉降过程还是扩散过程，凝并作用总是发生的。凝并虽然能减小粒子浓度，但不会降低粒子质量浓度，因为它是粒子浓度的函数。当通过搅拌等作用时，理论上粒子浓度还可以恢复。当粒子在0.1～1μm范围内时，沉降、扩散和凝并作用都发生，但其综合作用的数学模型至今尚未建立。