点火时间方程的计算方法

虽然用试验方法在特定的情况下可靠地测定点火的难易程度具有实际价值，但发展点火机理的分析模型也是极为重要的。通过文献的收集，发现D.M.Johnson已做出这样的模型。他根据热传递的基本方程，并对发火点规定了以下定义：必须把一种已知固体药剂加热至点燃，并不再需要外部加热就可继续燃烧的那个温度。他导出了一个方程用来测定对点火有影响的有关变数。以下的推导是由J.H.Mclain做出的，它和Johnson的模型在侧重点和方向上是类似的，但遵循了极不相同的途径。事实上这两种处理都得到了有助于肯定其正确性的相同的方程。

如图8.2所示，一个物质的切片在其高温端x处的温度为T2，在其低温端x+Δx处的温度为T1。由于温差产生了热流动（ΔH）。切片的焓随时间t的改变率与流入与流出切片的热流速率之差相等：

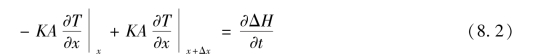
式中，K——热传导系数；

A——热流通过的面积。

因而：

式中，ρ——密度；

Δx——切片厚度；

c——比热。

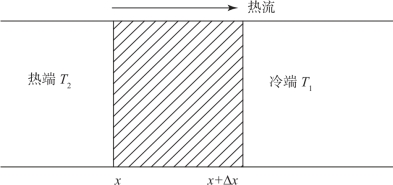
图8.2　热流模型

把式（8.3）代入式（8.2），并把式（8.2）中的第二项按泰勒级数展开，得出：

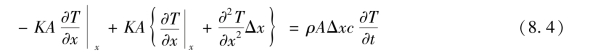
式（8.4）中的前两项互相消去后，式（8.4）的两边都除以AΔx，得出：

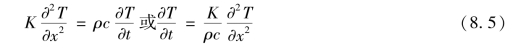
用扩散率α代替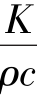后，则式（8.5）成为：

式（8.6）即热传递的基本方程。

现在解此方程，以确定在任何指定时间的切片温度。为此，假定了以下理想条件：整个切片表面是同时点燃的；没有辐射热损失；容器不产生热传导。

设定切片温度为变数y的函数：

式中

现在可以计算式（8.6）中的各项，首先限制每个xt的乘积须用y的幂表示。因此有：

将式（8.8）微分，得出：

由此，式（8.9）成为：

同样可得：

并得出：

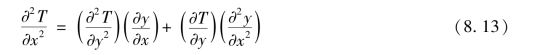
由式（8.8）得出：

因此有：

和

将式（8.16）和式（8.15）代入式（8.13），可以得出：

将式（8.17）和式（8.11）代入热流方程式（8.6），得出：

将式（8.18）的两边均除以nxtn-1，得出：

应用上述限制，即每个xt的乘积须用y的幂表示，xt-n-1必须是y的一次幂。因为x的指数为1，因此xt-n-1=xtn，n=-n-1和n=-1/2。方程（8.19）现成为：

由于y=xtn=xt-1/2，式（8.20）成为：

或

为了帮助解方程式（8.22），设参数P为：

可得：

将式（8.23）微分，得出：

或

将式（8.25）积分，得出：

现设Z2=y2/4α，即由于y=xtn=xt-1/2，得出：(www.xing528.com)

将式（8.27）代入式（8.26），得出：

通过对式（8.27）的分析，得出m和n的值如下：

当t→，Z→0；

当t→0，Z→；

当x→0，Z→0；

当x→，Z→。

因此，下限m为零，n可假定为零与无穷大之间的任何数值，例如n取时，方程式（8.28）成为：

现在计算常数C1和C2。当时间t接近于无穷大时，温度T接近于发火点Ti。由于当t接近于无穷大时，方程式（8.29）的积分上限接近于零，由此得出：

因此Ti等于C2，方程（8.29）成为：

当时间t接近于零时，温度T接近于环境温度Ta，Z接近无穷大。在这些边界条件下，式（8.31）成为：

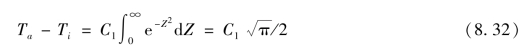
由式（8.32）得出：

将式（8.33）代入式（8.31），可以得出：

或：

将式（8.35）微分后，可以肯定这是对热方程式（8.6）的有效解法。方程式（8.35）也完全符合Johnson导出的方程。它使发火点Ti、时间为t时切片中间点x处的温度T、环境温度Ta（显然低于T和Ti）和扩散率α=K/ρC相互联系起来。

Johnson解此方程求得T，并把它微分后得出烟火药柱长度上x点处的温度梯度：

式中，t大于零，该点进入烟火药柱中的距离为x，而不是在药柱的两端。

一维的热流方程如下：

式中，qin——进入物质中的热流速率。

将式（8.36）代入式（8.37），得出：

当出现平衡条件时，T为常数（物质中x点处的温度停止变化），

的数量也必须等于某一常数：

然后有：

这等于说，燃烧速度（∂x/∂t）与恒温T时表面的传播速度是相等的。

将式（8.40）代入式（8.38），使指数减到e-G2。把此数简写为常数F，方程（8.38）则成为：

由上式可求解t，即恒定热流速率（qin）下的点火时间：

但扩散率α等于K/（ρc），所以式（8.44）成为：

式（8.45）即为点火时间方程。

设烟火药点火能E为：

以此取代式（8.45）中的t，则得出点火能量方程：

点火时间方程告诉了我们许多物理数据，这些数据通常与由经验和直观所预料的一致。当导热系数高（热消散快）、密度高（需加热更多的质量）、比热大（升温时每单位质量所需的热量较多）、截面积大（对质量和热损失两者都有影响）和发火点Ti高（需要较大的升温）时，所需的点火时间也较长。当热流速率（qin）高时，因有更多的热可用于升温，所以点火时间较短。

上述点火方程可以用来讨论高低温下点火能量问题，也可以计算在高温和低温下点燃某种药剂所需要的相对能量。例如，若某种药剂的发火点Ti为300℃，那么在30℃和-50℃时的点火时间之比是：

这也说明，在较高温度下点燃药剂所需的能量仅为在较低温度下所需的60%。

点火方程也指出了点火能量不足的不良后果。若只有部分药剂点燃，则放热较慢，从而造成加热速率降低。如果加热速率降低1/2，点火时间则需增加4倍。需要指出的是，药柱压药密度不均匀的未压紧部位、某些导热好的装药容器壳壁及燃烧面变小的制品均易造成供热速率降低，达不到连续稳定燃烧所需的水平，将会引起瞎火或不稳定燃烧。

将点火方程加以变换，则有：

式中，B——变换系数。

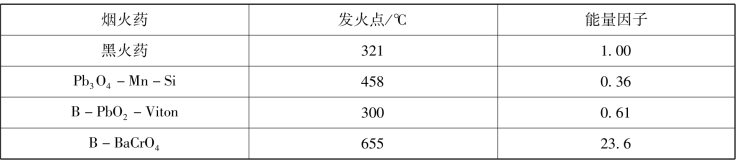
能量因子的大小可以用来比较烟火药的点火感度。几种药剂的能量因子和发火点（黑火药的能量因子假定为1.00）见表8.7。由表中数据可知，Pb3O4-Mn-Si药剂的能量因子较低，所以有较高的发火感度。尽管它的发火点高于黑火药，但它比黑火药更易于被热火花点燃。这与McLain和Frahm的发现是一致的，即含四氧化三铅的药剂比黑火药更易于用热火花点燃。

表8.7　烟火药的能量因子

思考题：

1.简述铁铝高热剂的优缺点，并分析制造铁铝高热剂时为什么选用的是Fe3O4而不是Fe2O3。

2.烟火药的点火与哪些因素有关？如何解决难点燃烟火药剂的点火问题？

3.试分析点火药燃烧产物液态熔渣对点火能力和燃烧速度的影响。