照明剂燃烧和火焰辐射的机理解析

7.1.7.1　钠盐照明剂的燃烧机理研究

很多学者对NaNO3-Mg钠盐照明剂的燃烧机理开展了研究。有关钠盐照明剂中NaNO3的分解过程，研究者认为如下：

接着：

这两个阶段的反应都是吸热的（式中M为金属还原剂）。

NaNO3-Mg混合物的化学反应与着火过程是NaNO3首先分解成NaNO2+O，O原子将Mg氧化成MgO，反应剧烈放热；然后NaNO2进一步分解成NaO+N2+O2，促使Mg进一步氧化。最后的产物是NaO和MgO。

麦克莱恩（Mclain J.H.）研究了钠盐照明剂高温反应的反向问题。他在NaNO3-Mg-聚酯树脂照明剂燃烧产物中测出了CO，而其主反应是：

他认为CO是由照明剂燃烧产物MgO与C的可逆反应产生的：

根据ΔH=TΔS算得可逆温度Trev：

可逆温度具有抑制作用，即NaNO3-Mg反应升至可逆温度（1 860℃）时，系统吸热，限制钠盐照明剂的燃速和温度进一步升高。

目前有关照明剂燃烧机理的研究尚不透彻，燃烧物理模型和数学模型尚未很好地解决，燃烧面的界面化学物理过程研究也不完善，还需要进一步努力。

7.1.7.2　照明剂火焰辐射机理研究

70年代以来，人们在进一步提高照明剂性能的研究中遇到了困难，开展了照明剂火焰辐射机理研究。（美）杜达（Douda B.E.）最先系统地开展了有关辐射传播的研究。他首先假设镁、硝酸钠和黏结剂火焰的辐射通量主要由钠D线共振跃迁的光子组成。关于火焰辐射传播方程按图7.3所示的物理模型进行推导。取火焰气体厚度为dz，其横截面积为dσ，辐射强度为Iv的单色射线投射到体积元dzdσ的下表面上，沿s方向为火焰外观察者的正方向，s与垂直轴N的夹角为θ，Iv经过辐射介质层的变化量为dIv。

图7.3　辐射平衡分析用物理模型

本模型假设火焰气体是均匀的，瑞利散射忽略不计，因此辐射平衡只涉及散射与吸收，故有：

介质吸收所损失的强度增量为：

式中，Kv——线性吸收系数；

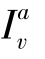中上标a表示吸收。

体积元发射频率为v，其辐射能量是：

式中，εv——通过单位立体角dω并经过dt时间间隔的单色体积元dσ的发射系数。

又发射光强度增量的辐射能量（中上标e表示发射）可表示为：

由式（7.18）和式（7.19）得到发射系数εv：

由式（7.17）得：

综合式（7.20）和式（7.21）可得：(www.xing528.com)

将式（7.16）代入式（7.22），则有：

式中，μ=cosθ。

为了数学处理上的方便，将发射系数εv与吸收系数Kv结合，并定义为源函数：

若将单色光学厚度定义为：

将式（7.23）除以Kv，并利用式（7.24）和式（7.25），则得到辐射传播微分方程：

若引进吸收系数的归一化函数Φv：

即

将式（7.28）代入式（7.26），则得到辐射传播方程的另一形式：

若对式（7.29）两边除以μ，并同时乘以exp（-τΦv/μ），同时定义τ1、τ2为火焰从前到后的光学深度积分限，且Iv1、Iv2为对应的光谱强度，则辐射传播积分方程为：

由此表明，在给定v和μ的情况下，火焰在任意τ1处的出射强度Iv1等于在τ2处入射的强度Iv2被τ2和τ1间隔衰减项加上被τ2和τ1间隔气体递增衰减的源函数的积分。

为了解出辐射传播方程，对火焰模型做出如下假设：

（1）火焰在平行层面是均匀的气态物质；

（2）气态物质由惰性分子加上能激发到2p1/2和2p3/2水平上的钠原子组成；

（3）存在由局部温度控制的局部热力学平衡；

（4）辐射引起的能量交换导致辐射平衡；

（5）介质的折射率为1；

（6）辐射在发射时是未极化的，在与火焰物质相互作用时仍保持未极化；

（7）温度梯度可以用一个顶点在火焰中心的抛物面来表示；

（8）钠原子吸收函数Φva和数量密度N0在火焰中是一个与τ无关的平均值。

在这些假设的基础上简化方程，可以得到单色出射强度为：

式中，ϕva——理论光谱辐射能；

Bv（T）=Sv（τ）——黑体辐射能量的普朗克函数；

T——光学厚度τ处的火焰温度。

式（7.31）表明ϕva与光谱出射强度是成正比的，进行归一化，即可获得光谱分布图。杜达对三种配方在八个压力下的燃烧进行了计算，并分别开展了试验，结果表明，计算与试验基本吻合。

1976年德里赫（Dillehay D.R.）扩展了杜达模型，对混进火焰的环境气体及辐射能沿火焰轴的损失做了考虑，从而完善了杜达的模型。还有一些学者从分子、原子结构角度研究了辐射理论。