7.1.6.1 照明剂的照度
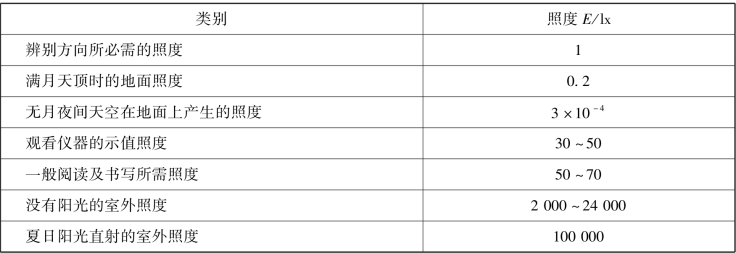
照明剂的照度是指照明剂燃烧所发射出的可见光照射在被照射目标单位面积上光通量的大小。照明剂的照度值越大，供人眼观察的目标越清楚。表7.13列出了一些典型情况下的照度值。
表7.13 几种典型情况下的照明值
在空中燃烧着的照明炬可视为点光源，如图7.2所示。
被照明平面上任一点M的照度Ei与光源强度I及光源入射角α的余弦成正比，而与光源和M点间距离l2成反比：
因为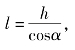
所以上式又可以写作：
式中，Ei——照度，lx；
I——照明炬发光强度，cd；
h——照明炬在空中悬挂高度，m；
α——光源入射角。
可见，光源对地面垂直投影处（即被照明圆面积中心）照度值最大，离中心越远，照度值越小。
7.1.6.2 最大照明半径与发光强度及照度的关系
当照明炬发光强度和悬挂高度一定时，照明半径R仅与边缘照度Em有关，其值可以根据照度定律和图7.2中的几何图求得。
因为
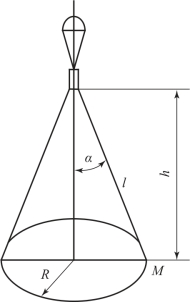
图7.2 点光源的照明
又因为
所以
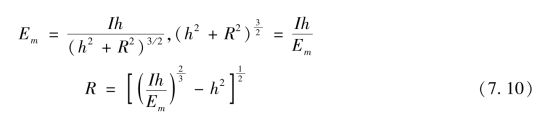
式中，Em根据使用要求确定，可以取各种值。要求Em大时，R则小，而要求Em小时，R则大。因此，评价照明半径时，必须以一定的Em作为前提。通常取Em=0.5 lx（即比满月时在月光照明下亮2.5倍）作为比较条件。
照明炬是在吊伞制动下逐渐降落过程中进行照明的，悬挂高度h自上而下变小。照明炬的发光强度I在燃烧过程中变化可近似看作定值。当要求Em一定时，R将随着h改变，其变化规律是随悬挂高度下降R逐渐增大，至某一高度hm时，照明半径R达一最大值Rmax，然后高度继续下降，R又逐渐减小，直至照明炬接近地面时减为零。
高度hm称为照明炬的最佳悬挂高度，其对应的最大照明半径用Rmax表示。根据式（7.10），令
则可求出照明炬最佳悬挂高度hm和相应的最大照明半径Rmax：
在I和Em给定的条件下，为了获得较大的照明半径，应使照明炬燃烧接近一半时通过最佳悬挂高度，这样吊伞照明系统能够在有利悬挂高度范围内停留较长时间，由此得出照明弹的有利空抛高度hk为：
式中，hm——照明炬最佳悬挂高度；
vpi——吊伞照明系统平均下降速度；(www.xing528.com)
t——照明炬空中燃烧时间；
ΔyH——空抛至开伞点吊伞照明系统降落高度，
LH——空抛至开伞点吊伞照明系统运动距离，通常LH=50 m；
|θk|——空抛点弹道倾角。
7.1.6.3 照明炬高度与照明半径的关系
在最有利的入射角α时的照明炬高度h与照明半径R的关系，按照度定律和图7.2中的几何图又可以推导出：
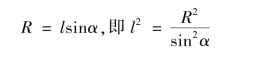
代入式（7.8），得：
令
则
由于
所以
即
显然，当sinα=0时，得到一最小照度Emin；当3cos2α-1=0时，得到一最大照度Emax，即
此时，求得照明炬的高度与照明半径的关系为：
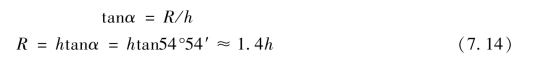
7.1.6.4 能见距离
能见距离是指能看清楚目标的基本外形时观测点至目标之间的直线距离，又称最大识别距离。影响能见距离的因素很多，除照度E外，还有气象、时间、地形条件和目标种类等。如果忽略大气对光线的吸收，被照目标的能见距离D1为：
式中，L——目标宽度。
实际能见距离D可根据表7.14中D1和ψ用插值法求得。
表7.14 能见距离表
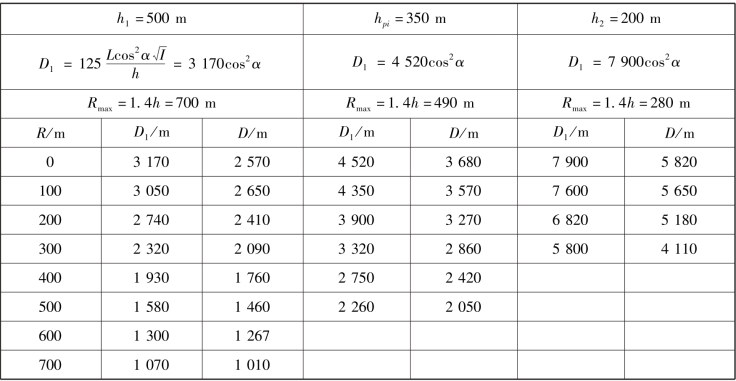
例7.2 求被照明区域各个不同点上目标的能见度。已知照明炬发光强度I=4×105cd，照明炬在空中的悬挂高度开始为h1=500 m，燃烧完后为h2=200 m，平均悬挂hpi=350 m；晴天ψ=0.9；目标宽度L=20 m。
解：计算结果见表7.15。
表7.15 各个不同点上目标能见度计算结果
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
