朗伯定律对于大多数辐射源是否有影响？

6.2.2.1　朗伯定律

对于大多数发光物体，不论其发光表面的形状如何，在各个方向上的亮度都相等。例如我们看到的太阳是一个圆球，但人眼的感觉是中心和边缘一样亮，和看到一个均匀发光的圆形平面相同。下面讨论辐射体在各个方向的亮度及不同方向上光强变化的规律。

设dA为一发光面，由亮度的定义可知，在与法线成θ角方向上的亮度为：

式中，Iθ——θ方向上的发光强度，如图6.5所示。

同理，在法线方向上的亮度为：

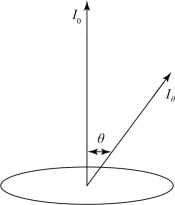
图6.5　发光强度示意图

如果发光面或漫射光表面的亮度不随方向改变，则在法线方向和成θ角方向的亮度相等，因此有：

即

上式为朗伯定律（或发光强度的余弦定律）的数学表达式。

遵从朗伯定律的光源称为朗伯光源，它的亮度不随观察方向改变而变化。严格地讲，只有绝对黑体才是朗伯光源。被均匀照明的烟熏的氧化镁表面、毛玻璃和乳白玻璃表面，都可近似地看作遵从朗伯定律的光源。

自然界中，我们所看到的大多数物体本身并不发光，而是被光源照射后，光线在物体表面进行漫反射。现在讨论遵从朗伯定律本身不发光物体的表面亮度问题。

设一遵从朗伯定律的漫射光表面dA，它的光照度为E，根据光通量和光照度之间的关系，面积元dA所接收到光通量为：

设漫射光表面的漫射系数为ρ，面积元dA反射出来的总光通量为dφ′，则：

根据朗伯定律，漫射光表面的亮度不随方向改变。因此，漫射光表面所发出的总光通量和亮度之间的关系为：

将dφ′=ρEdA代入，则得：

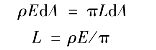
根据光出射度和光照度之间的关系，可以写为

即单位面积发射的光通量为其亮度的π倍。因此，只要测出漫射光表面发射的总光通量，就可以计算出发光面在各个方向上的光亮度。

光辐射传播过程的能量损失对光通量和光亮度有着重要的影响。现讨论如下。

如两个面积元dA1和dA2的中心连线OO′的距离为l，两面积元的法线与中心连线之间的夹角分别为θ1和θ2，设两面积元沿OO′方向所传递的光能量均投射在相应面积元dA2和dA1上，即光能量无外溢，也无损失，两面积元的光亮度分别为L1和L2，如图6.6所示。则由dA1发射到dA2上的光通量为：

根据几何光学中光线的可逆性原理，相应dA2发射到dA1上的光通量为：

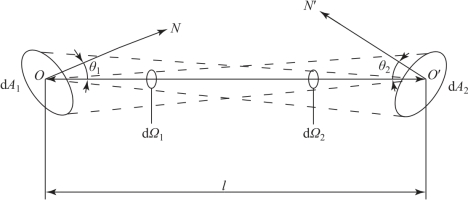
图6.6　光辐射传播示意图

假设光辐射在所限定的空间内传播时无能量损失，则：

相应可以得到：

从以上讨论可知，光辐射在同一均匀介质和限定空间内传播时，如果无能量损失，则在传播方向上任一截面上的光通量和光亮度均保持不变。如果光辐射在传播过程中有能量损失，则Φ21≠Φ12，相应L1≠L2。

如果dA1为发光面，dA2为接收面（如光电探测器表面），则由dA1发射、dA2接收到的光通量为：

式中，L——发光面的光亮度。(www.xing528.com)

从该式可看出，只要测得dΦ，就可以计算出光亮度。特别是发光面遵从朗伯定律时，其计算更简单。

6.2.2.2　两种典型光辐射量的计算

任何辐射源都有一定尺寸，不可能是一个几何点。所谓点源、面源，不是根据辐射源尺寸大小来划分的，而是根据辐射源面积是否充满仪器的测量视场。如果辐射源的面积小于仪器视场，辐射源面积都是有效的，这样的辐射源称为点源。当一个红外搜索系统对远方来袭导弹的张角远小于系统瞬时视场角时，尽管测到的辐射可能来自导弹的蒙皮、喷管或尾焰，可以认为全部辐射来自一点。此时可以按照点源计算产生的辐照度。当在近距离用热像仪测量导弹的尾焰辐射特性时，可以得到尾焰温度场空间分布的热图像。尾焰热像由许多像素组成，每个像素的测量视场很小，它不能探测到全部尾焰。此时尾焰辐射面积只有部分是有效的，应按面源计算产生的辐照度。

一、点光源照度的计算

点光源的特点是向周围4π空间以相同的发光强度发出光辐射，如图6.7所示。设辐射源为点源O，辐射源O到受照微面元为dAs。中心所引的径向量r与该面法线成θ角，从点源看，受照微面元dAs所张的立体角为dΩ，根据辐射强度定义，有：

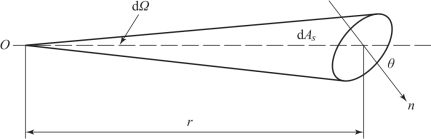
图6.7　点辐射示意图

式中，Φ——辐射通量；

I/r2——点光源垂直于传播方向上被照表面的光照度，用E0表示，E0为光线以倾角θ斜射到被照面的光照度，即

由上式可以看出，当θ角为零时，照度值最大。随θ角不断增大，照度值将变小。该公式就是照度余弦定律。照明工程中，在计算各种物体表面的光照度或用照度计直接测量光照度时，必须考虑由θ角的变化所带来的测量和计算误差。当被辐照面法向指向点源时，cosθ=1，则有：

根据上式可以由辐照度E值计算出光辐射强度I。

光辐射源在被辐照面积上产生的辐照度与该点源辐照强度I成正比，与离点源距离r的平方成反比，这被称为距离平方反比定律。此定律包含了发光强度、照度和光通量三个常用量之间关系，在光度学和辐射度学中广泛应用，具有十分重要的意义。

应该指出，点源实际尺寸不一定很小，而是按辐射源线度尺寸与接收面距离的比例来区分是点源还是面源的。距地面遥远的一颗星，实际尺寸很大，但观察者看到的却是一个“点”。同一辐射源在不同场合，既可以是点源，又可以是面源，例如飞机的尾喷管，在1 km以上距离测量时，是点源；在3 m的距离测量时，则表现为面源。通常认为，当距离比辐射源线度尺寸大10倍以上时，就可以看作点源。

二、面光源照度的计算

任何实际光源都有一定的尺寸或发光面积，因此不能直接利用上面的公式计算受照面的强度，否则会产生一定的误差。

设一圆盘形余弦辐射源半径为R、面积为S0、亮度为L，如图6.8所示，距其l处为一受照面的小面元Ad。该面光源上的面元dS沿l向Ad发出的光通量为：

图6.8　面光源辐射示意图

式中，，代入上式得：

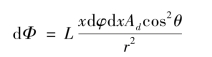
由图6.8可知：

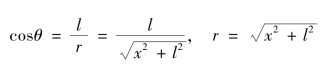
则得到：

该面光源向小面积Ad发出光的总通量为：

令x2+l2=u，则代入上式，有：

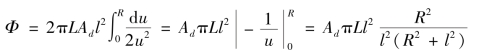
按照定义，可得面光源S0在Ad面上引起的照度为：

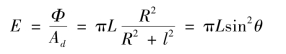
上式也可写为：

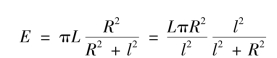
其中，πR2为面光源的面积S0，而L·S0为该面光源的发光强度I，所以上式变为：

其中，I/l2可视为点光源在面积Ad上产生的辐射强度。

因此，计算面光源的辐射照度时，如果采用点光源公式，产生的误差为：当R/l<1/10时，小于1%；当R/l<1/15时，小于0.5%。可以根据误差要求选择测试距离。

可见，对于圆盘形辐射体，其被辐照面积Ad上所产生的辐照度与辐射强度I、圆盘形辐射面S0与被辐照面Ad之间的距离l及圆盘形辐射面S0的半径R有关。