黑体辐射定律探究与分析

黑体是一个能完全吸收入射到它上面的辐射能的理想物体，在辐射度学中占有十分重要的位置。只有黑体光谱辐射量与温度之间存在精确的定量关系。光辐射度量的绝对值无法直接测量，它们常常转换成一些可测物理量（如电量、热量等）进行测量。因此，黑体温度的测量起到了确定辐射度量的作用，即黑体辐射在辐射度学中起到了基准作用。现实世界中许多光源可以认为或近似认为是黑体，例如太阳、月亮、地球、星星等。另外，还有许多光源和辐射体，尽管它们的辐射特性和黑体相差很大，甚至还有吸收带，但也常用与黑体相当的某些特性来近似表征。

6.1.3.1　吸收、反射、透过率

如果辐射到某一物体的总功率为P0，其中一部分Pa被吸收，部分Pρ被反射，另一部分Pτ穿透该物体，如图6.2所示，则：

将上式两边各除以P0，得：

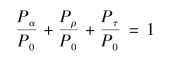
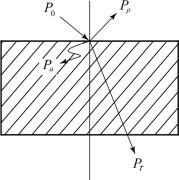
图6.2　吸收、反射和投射示意图

上式左边第一项比值称为物体的吸收率α，第二项称为物体的反射率ρ，第三项则称为物体的透过率τ，则：

一种材料的吸收率α、反射率ρ和透过率τ是指对该材料的标准试样（规定了表面处理、表面粗糙度及厚度等条件的试样）进行相应测试得到的数据。当具体试件的表面状态、厚度等不同时，所得测试数据可能会与标准试样的数据相差很大。为了区别这两种情况的数据，目前国际上已经习惯将标准试样的数据称为吸收率、反射率和透过率；而将具体试件的相应数据称为吸收系数、反射系数和透过系数。

由上式可知，若α=1，则ρ=τ=0，这意味着所有落在物体上的辐射能完全被该物体吸收，这一类物体称为绝对黑体或简称黑体；若ρ=1，则α=τ=0，所有落在物体上的辐射能完全被反射出去。如果反射的情况是正常反射，即符合几何光学中反射定律规定的反射角等于入射角，该物体称为镜体；如果是漫反射，则该物体称为白体；若τ=1，则α=ρ=0，此时不存在绝对黑体、绝对白体和绝对透明体。α、ρ、τ的值与物体的材料、表面状况、温度及辐射线波长有关。例如，石英玻璃对λ>4μm的红外线是不透明的，但对λ<4μm的红外线则透过率很好；普通窗玻璃则不然，它仅仅是可见光的透明体，几乎不让紫外线和红外线通过。对吸收和反射来说，也存在上述情况。白色表面能很好地反射可见光，但不管什么颜色的油漆，在红外区的吸收率均很高。对红外线辐射的吸收和反射具有重要影响的不是物体表面的颜色，而是表面材料、表面粗糙度等。不管什么情况，光滑表面要比粗糙表面的反射率高几倍。

要想增加物体的吸收率，通常把物体表面蒙上一层不光滑的黑色涂料。即使这样，也只能吸收百分之九十几，它还不是黑体。一个空腔壁面上的小孔具有接近绝对黑体的性质（如图6.3所示）。投射进这种小孔内的能量，经过许多次的吸收、反射后，才可能有一丝的能量从孔中漏出去。对小孔而言，投射进去的辐射线基本上被吸收掉了，可以认为它的吸收率α=1。红外测试中经常用到的作为标准辐射源的黑体炉就是基于这一原理制成的。工业中作为标准辐射源的黑体炉，其常见的腔型如图6.4所示。

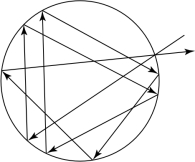
图6.3　黑体原理示意图

图6.4　常见黑体炉的腔型

（a）～（c）圆锥腔；（d）、（e）具有光滑和波纹底部的圆柱腔和匣形腔；（f）球腔

6.1.3.2　普朗克定律

1879年，斯蒂芬从他的试验测量中得出结论：黑体辐射的总能量与其绝对温度的四次方成正比。1884年，玻尔兹曼应用热力学的关系也得到同样结论。这个结果就是熟知的斯蒂芬-玻尔兹曼定律。1894年，维恩发表位移定律，给出了黑体辐射光谱分布的一般形式，遗憾的是，它仅与低温时短波段的试验数据相符。1900年，瑞利基于经典物理的概念，推导出与高温时长波段试验数据相吻合的表达式，可是表达式预言能量随波长减小会无限增加，被人称为“紫外灾难”。

1900年，普朗克发表了辐射定理，用量子物理的新概念补充了经典物理理论，完整叙述了黑体辐射的光谱分布。普朗克定理指出，黑体的光谱辐出度Mλ与波长λ及温度T的关系可表示为：

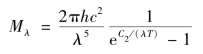
通常也可以写为：

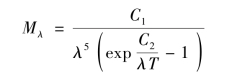(www.xing528.com)

式中，Mλ——绝对黑体的光谱辐射出射度，W·cm-2·μm-1；

λ——波长，μm；

T——绝对温度，K；

C1——第一辐射常数，3.741 8×10-12 W·cm-2；

C2——第二辐射常数，1.438 84 cm·K。

普朗克定律描述了黑体辐射的光谱分布规律，揭示了辐射与物质相互作用过程中和辐射波长及黑体温度的依赖关系。随黑体温度增加，其光谱辐出度迅速增加，光辐射的峰值波长向短波方向移动。另外，不同温度的光谱分布曲线彼此不相交，说明任何波长的光谱辐出度都随温度的升高而增加。

波段的光谱辐出度可以用积分方法求得：

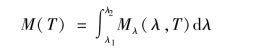
可以借助黑体辐射表计算波段辐射出射度。由于黑体辐射表给出的是0～λ的辐射出射度，做变换求得结果为：

例如，热成像系统经常用到常温黑体（300 K）在8～14μm的辐射出射度，可有：

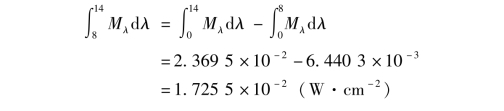
6.1.3.3　斯蒂芬-玻尔兹曼定律

从零到无穷大的波长范围内，对普朗克光谱分布函数积分，可以得到黑体辐射到半球空间的辐射通量密度：

式中，M——黑体的总辐射出射度，W·cm-2；

σ——斯蒂芬-玻尔兹曼常数，5.670 32×10-2 W·cm-2·K-4。

斯蒂芬-玻尔兹曼定律表明，黑体在单位面积单位时间内辐射总能量与黑体绝对温度的四次方成正比。因此，相当小的温度变化都会引起辐射能量的较大变化。

6.1.3.4　维恩位移定律

求普朗克光谱分布函数对波长的偏微分，并令其为零，可得黑体的光谱辐射出射度的峰值波长λm和黑体绝对温度T之间的关系，即

维恩位移定律指出，当黑体温度升高时，其光谱辐射峰值波长向短波方向移动。在实际可以达到的温度范围内，光谱辐射峰值波长均位于红外区域。如300 K室温条件下，峰值波长为9.66μm，因此，8～14μm红外波段有时也称为热红外波段。峰值波长的光谱辐射出射度与绝对温度的五次方成正比，即

式中，b为1.286 2×10-11W·m-2·μm-1·K-5。