度量辐射和光度的参量：详解与应用

在可见光范畴，已经有完善的光度学术语和计量单位，如光通量单位为流明（lm）、发光强度单位为坎德拉（cd）及光照度单位为勒克斯（lx）等。光度学物理量主要根据光学引起观察者的视觉感知来计量，其度量单位不由质量、长度和时间等最基本的物理单位构成。

辐射学的物理量用辐射能量度量，其辐射术语可应用于整个电磁频谱，包括微波、红外、紫外和X射线等谱段。如果将辐射量转换为光度量，必须计入人眼视觉特性，如1 W辐射通量相当于多少流明光通量，这就与视见函数有关。

6.1.1.1　视见函数

把对人眼最灵敏的波长λ=555 nm的视见函数规定为1，即V（555）=1（视见函数的最大值）。假定人眼同时观察两个位于相同距离上的辐射体A和B，这两个辐射体在观察方向上的辐射强度相等，A辐射的电磁波长为λ，B为555 nm，人眼对A的视觉强度与人眼对B的视觉强度之比，作为λ波长的视见函数V（λ），V（λ）≤1。有了视见函数，就能比较两个不同波长的辐射体对人眼产生视觉的强弱。例如，人眼同时观察距离相同的两个辐射体A和B，假定A、B在观察方向上的辐射强度相等，辐射体A的辐射波长为600 nm，B为500 nm，根据“明视觉视见函数国际标准”表可查得，V（600）=0.631，V（500）=0.323，这样辐射体A对人眼产生的视觉强度是辐射体B的0.631/0.323倍。反之，欲使辐射体A和辐射体B对人眼产生相同的视觉强度，则辐射体A的辐射强度应该是辐射体B的辐射强度的一半。

6.1.1.2　立体角Ω

立体角Ω是辐射度学和光度学中十分重要的概念。它是描述辐射能向空间发射、传输或被某一表面接收时会聚或发散的角度。定义：以锥体的顶点O为球心作一球表面，该锥体在球面上所截取部分的表面积S和球半径r平方之比，如图6.1所示。(www.xing528.com)

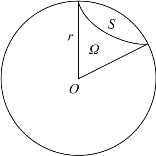
图6.1　立体角的概念

立体角的单位是球面度（sr）。

半径为r的球的表面积等于4πr2，所以一个光源向整个空间发出辐射能或者一个物体从整个空间接受辐射能时，相应立体角为4π球面度。求空间任一表面S对空间某一点O所张的立体角，可由O点向空间表面S的外边缘作一系列射线，由射线围成的空间角即为表面S对O点所张的立体角。不管空间表面凸凹如何，只要对同一点O作射线束围成的空间角是相同的，那么它们就有相同的立体角。