其他滤波方法在组合导航中的应用

惯性导航系统的初始对准有两种方案：采用回路反馈法实现的经典对准方案；采用卡尔曼滤波或递推最小二乘法实现的广义数字信号处理方案。无论是对准精度还是对准时间,后者都明显优于前者。在捷联式惯性导航系统中,采用最优估计理论进行初始对准,就是估计惯性导航系统的失准角,从而修正姿态矩阵。

利用卡尔曼滤波技术进行初始对准和组合导航的方法已经在9.4.2节和9.4.3节已经进行了介绍,下面将简单说明其他卡尔曼滤波技术在初始对准和组合导航上的应用。

9.4.4.1　自适应卡尔曼滤波在组合导航中的应用

根据第4章介绍的自适应滤波数学模型,以某型高速旋转稳定弹为例,利用GPS模拟数据和惯导解算模拟数据进行仿真验证。东北天向位置和速度初始对准结果如图9.16、图9.17所示,其中,GPS输出结果分别为接收机输出东北天位置或速度,捷联解算结果分别为MIMU 捷联解算出的东北天位置或速度,滤波修正结果是经过卡尔曼滤波修正后的东北天位置或速度。GPS数据误差为GPS 输出数据与对应参数真实值之差,滤波估计误差是经卡尔曼滤波修正后的捷联解算结果与真实值之差。

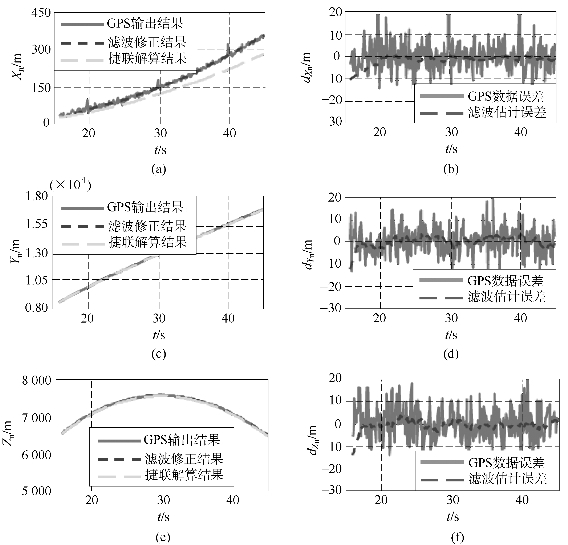
图9.16　东、北、天位置滤波结果(书后附彩插)

(a)东向位置滤波结果；(b)东向位置滤波误差；(c)北向位置滤波结果；(d)北向位置滤波误差；(e)天向位置滤波结果；(f)天向位置滤波误差

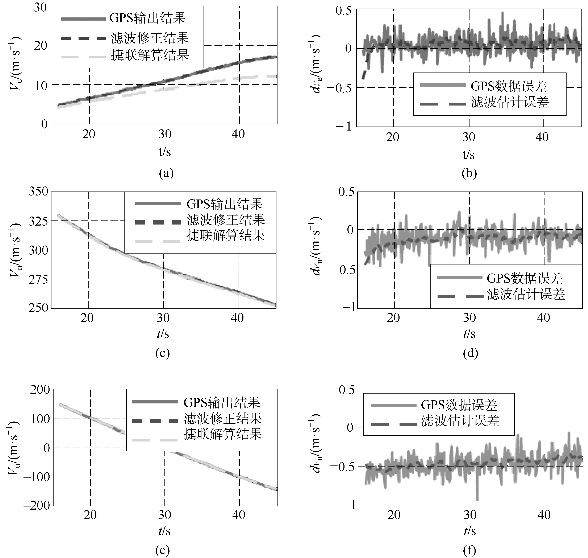
图9.17　东、北、天速度滤波结果(书后附彩插)

(a)东向速度滤波结果；(b)东向速度滤波误差；(c)北向速度滤波结果；(d)北向速度滤波误差；(e)天向速度滤波结果；(f)天向速度滤波误差

从图9.16所示的位置初始对准结果可以看出,与离散卡尔曼滤波相比,自适应卡尔曼滤波更能适应模型变化,降低模型误差干扰,使滤波校正后的位置误差更低,实际位置误差不大于2 m。由图9.17所示的速度对准结果可知,与离散卡尔曼滤波相比,自适应卡尔曼滤波的速度滤波结果校正效果比较明显,其速度误差不大于0.2 m/s。

旋转稳定弹的俯仰、滚转和偏航姿态初始对准结果分别如图9.18～图9.20所示。其中,捷联解算结果为捷联解算出的姿态数据,实际姿态为所采用弹道数据的真实姿态,滤波修正结果是经过卡尔曼滤波修正后的姿态数据,捷联解算误差是捷联解算姿态与真实姿态之差,误差校正结果是经卡尔曼滤波修正后的捷联解算姿态与真实姿态之差。而且,与离散卡尔曼滤波相比,自适应卡尔曼滤波可以适应模型变化,大幅提高弹丸姿态估计精度,经误差修正后,姿态数据误差不大于±0.5°。

从自适应卡尔曼初始对准滤波结果可以看出,与离散卡尔曼滤波相比,自适应卡尔曼滤波对系统模型精确程度和系统误差模型及观测误差模型的要求较低,其精度和稳定性更好,能适应由传感器故障或外部条件改变而引起的有限数据突变,更适合于具有高动态特性的旋转稳定弹组合导航系统初始对准。总之,利用自适应卡尔曼滤波对旋转稳定弹GPS/MIMU组合系统进行初始对准,在初始对准模型和误差模型较为接近真实模型时,其初始对准精度和稳定性较好,基本满足初始对准要求。然而,旋转稳定弹运动状态比较复杂,其高动态运动过程中也容易出现状态突变或测量系统短时失效而导致的粗大误差,进而可能导致自适应卡尔曼滤波精度下降(甚至发散)。

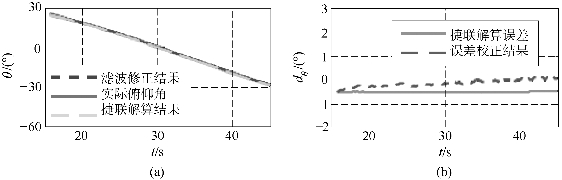
图9.18　俯仰角滤波结果(书后附彩插)

(a)俯仰角滤波结果；(b)俯仰角滤波误差

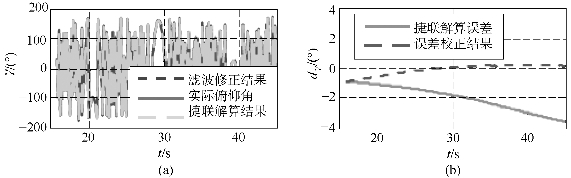
图9.19　滚转角滤波结果(书后附彩插)

(a)滚转角滤波结果；(b)滚转角滤波误差

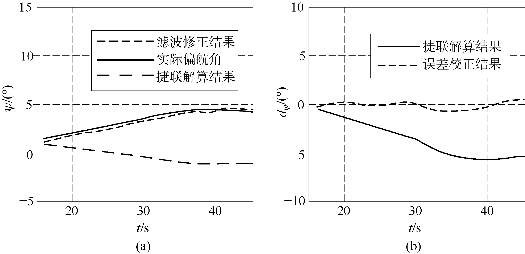
图9.20　偏航角滤波结果(书后附彩插)

(a)偏航角滤波结果；(b)偏航角滤波误差

9.4.4.2　联邦滤波在GPS/INS组合导航上的应用

GPS/INS联邦滤波的简化结构如图9.21所示。

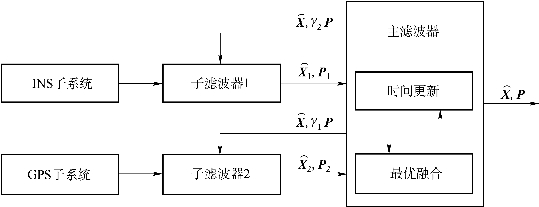
图9.21　GPS/INS联邦滤波的简化结构(www.xing528.com)

根据第4章介绍的联邦滤波的理论,将子滤波器和主滤波器的初始估计协方差矩阵设置为组合导航系统初值的γ1＝γ2＝γm＝1/β倍,将子滤波器和主滤波器的过程噪声方差阵设置为组合导航系统过程噪声方差阵的γ1、γ2倍,各子滤波器各自处理自己的量测信息,获得局部估计。在得到各子滤波器的局部估计和主滤波器的估计后,按下式进行最优组合。然后,用全局滤波解来重置各子滤波器和主滤波器的滤波值和协方差阵。

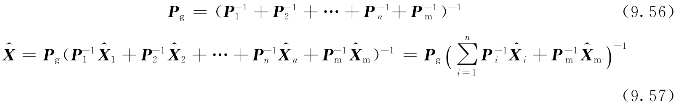
联邦滤波状态方程的构建一般有两种方法：公共状态法和完全状态法。

公共状态法只使用各滤波器均处理的公共状态作为状态量,在组合导航系统中,若INS作为基准公共导航系统,那么就使用INS的状态量来作为系统状态量,使用INS的状态方程来作为系统方程,其状态方程的建立与式(9.4)一样。

完全状态法是指所有导航系统的状态方程联立为系统状态方程,其中GPS状态量XGPS为GPS解算的纬度、经度、高度误差和东北天的速度误差值,即

其状态方程为

使用公共状态法会损失系统信息,因为仅以公共状态为状态量,各自系统的独自信息都不能进入融合系统,也不能在融合中更新,估计将是次优的,但这种方法构建的状态量维数低、计算量小,很实用。使用完全状态法在理论上是优越的,但是从实际的角度看,组合导航系统的状态维数将很多,实时性下降,计算量增大,故障的可能性也将提高。

同理,联邦滤波量测方程的构建也有两种方法：总体观测法；局部观测法。

总体观测法通常将观测量的差值直接作为观测量。例如：

局部观测法将各系统的误差的差值作为观测量。例如：

这两种方法的核心区别是对观测噪声的认识和处理阶段。从使用角度来看,总体观测法将观测差值归于一个系统的误差中,只需使用一个系统的状态量(通常是公共系统),因此总体观测法既可以与公共状态法配合,也可以与完全状态法配合。局部观测法需要使用两个系统的状态量,通常与完全状态法配合。

9.4.4.3　神经网络在组合导航上的应用

神经网络包含许多相互连接的层结点,在不知道传感器特性的情况下,可训练一个神经网络融合传感器的信息。利用神经网络技术,以多个测量值为输入样本值,通过神经网络获取系统的误差状态估值,然后利用“分离定理”来实现系统反馈控制,以便快速补偿系统误差,从而提高系统实时性。应用神经网络进行状态估计的最大特点是数据实时处理,可并行计算,速度较快,对组合导航系统的模型结构以及统计特性没有具体要求,但对神经网络的在线训练是一个难点。杨莉、王新龙等采用多层神经网络代替卡尔曼滤波器来实现惯性导航初始对准,仿真结果表明,应用神经网络的惯性导航初始对准简化了运算的代数结构,提高了状态估值运算的实时性能,对准精度与卡尔曼滤波器相当。由于神经网络的学习功能和模糊推理系统的推理功能的融合不但能使系统具有自学习、自适应的特性,而且能提高系统的性能(如抗干扰能力、实对性等),因此将神经网络与模糊逻辑等用于信息融合目标跟踪定位也得到了人们的关注。

许丽佳等针对复杂环境引起的对系统干扰噪声的统计特性无法获得准确值的情况,引入了Elman神经网络对组合导航系统进行状态估计,其结构如图9.22所示。Elman神经网络具有较强的并行计算能力,且容错性高,当隐含层神经元足够多时,该网络可以保证以任意足够的精度逼近非线性函数。接下来,以文献[49]为例说明神经网络在组合导航中的应用。神经网络的训练过程：对同一状态量,给予不同的量测噪声集,然后把这些量测值用卡尔曼滤波器进行状态的最优估计,从而获得相应的状态估计值,将获得的这些状态估计值的平均值作为导航参数的真实值,并且作为Elman神经网络的期望输出样本,把量测值作为网络的输入样本,就可以对网络进行训练。

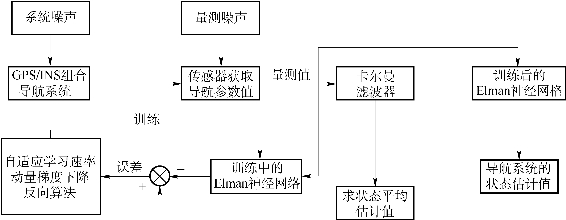
图9.22　GPS/INS神经网络组合导航系统

在滤波模型中,状态量取惯导解算的速度位置误差和失准角,测量值为惯导解算和GPS解算量之差,其滤波结构如图9.23所示。

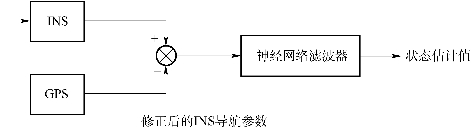
图9.23　神经网络滤波结构

例9-1以惯性导航系统的高度回路为研究对象,引入气压高度或卫星导航系统的测量高度,设计一个卡尔曼滤波器。分别列出滤波器的状态方程和量测方程,并给出滤波设计与计算的主要步骤。

基本思路：根据惯性导航系统的误差方程和GPS误差方程,写出滤波器的状态方程；将惯性导航系统输出的高度信息与GPS输出的高度信息相减,作为量测量,建立滤波器的量测方程。忽略惯性导航系统中的陀螺仪安装误差和加速度计安装误差。