伪距ρ(t)为信号接收时间tu(t)与第s颗卫星的信号发射时间ts(t―τ)的差值再乘以光在真空中的速度c,即
式中,t——GPS时间；
τ——GPS卫星信号到接收机的实际传播时间。
由于接收机时钟和卫星时钟不同步,所以将ρ(t)称为伪距。
分别考虑接收机时钟、卫星时钟与GPS时间的钟差,即
式中,接收机钟差δtu(t)的值是未知的；卫星时钟钟差δts(t)是已知的,可由播发出的星历、历书参数求得。
卫星信号在传播时,大气折射会造成传播延时,一般可分解成电离层延时I(t)和对流层延时T(t),为已知量。
考虑上述所有因素的影响,将第s颗卫星与接收机之间的真实距离用r(s)表示,可将伪距方程写为
式中,ερ(t)——随机误差项。
在GPS领域,时间量和长度量经常混淆使用,并省略时间标志。式(7.4)也可写为
并将未知量r、δtu移到等式同一侧,即
式中,ρc——校正后的伪距观测量。
假设未知量接收机的位置坐标为x＝[x y z]T,第s颗卫星的位置坐标为x(s)＝
则r(s)可表示为
不考虑随机误差项ερ,则GPS定位定时算法的本质就是求解下面这个四元非线性方程组：
当s≥4时,即可从上述方程组中求出4个未知量：x,y,z,δtu。
下面将介绍如何求解该非线性方程组。牛顿迭代法是用于求解非线性方程组的常用方法。首先,将各方程式在估计解处线性化；然后,利用最小二乘法求解该线性化方程,形成对偏差量的最优估计；最后,更新估计解的值,直到达到精度要求。
伪距定位算法的求解步骤如下。
第1步,准备数据,设置初始解。
(1)准备方程组所需的已知量数据,包括所有可见卫星在同一测量时刻的伪距测量值ρ(s),并计算校正后的伪距测量值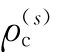
和卫星空间位置坐标[x(s) y(s) z(s)]。
(2)在进行迭代之前,还需要给出接收机初始位置坐标估计值[x0y0z0]T和初始钟差估计值δtu,0。如果在前一时刻已获得接收机的大致位置,则可以利用上一时刻的定位结果；如果是首次定位,则可以将初始值设置为0。
第2步,非线性方程组线性化。
函数r(s)对x的偏导可表示为
同理可得,r(s)对y的偏导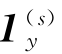
,对z的偏导
,非线性方程等式左边对δtu的偏导值为1。因此,第k次迭代时,方程组等式左边在
处线性化后为
式中,Xk―1＝[xk―1yk―1xk―1]T。
此时,线性化后的方程组可写为
写成矩阵的形式为
式中,
第3步,求解线性方程组。
利用最小二乘法,可得式(7.14)的解为(www.xing528.com)
第4步,更新非线性方程组的根。
第k次迭代后得到的接收机位置坐标xk和时钟钟差值δtu,k为
第5步,判断牛顿迭代的收敛性。
当第k次迭代得到的‖Δx‖或者
的值小于预设阈值时,则可以认为牛顿迭代已经收敛到了所需的精度,可以终止循环运算。
7.3.2.2 定位精度分析
考虑随机测量误差项
对定位精度的影响,则定位方程式可写作
式中,εx、εy、εz、εδtu——定位、定时误差量。
根据最小二乘法,可解得
为了计算定位误差的均值和方差,需要建立测量误差模型,该模型主要基于以下两点假设：
(1)各卫星的测量误差均呈均值为0,方差为
的正态分布。
称为用户测距误差(URE)的方差。
(2)不同卫星间的测量误差互不相关,即测量误差向量的协方差矩阵为对角矩阵。
基于上述假设,可推得定位误差协方差矩阵为
式中,H——权系数矩阵,表示为测量误差方差被放大的倍数,从而转变为定位误差方差。
根据协方差矩阵的定义,其对角线元素分别为各方向定位、定时误差分量的方差
,
,它与H矩阵对角线元素的关系为
则精度几何因子(GDOP)可定义为
位置精度衰减因子(PDOP)为
时间精度因子(TDOP)为
利用坐标转换矩阵,可以得到站心坐标系下的定位、定时误差量：
代入式(7.20),可得站心坐标系下的定位误差协方差矩阵为
则水平精度衰减因子(HDOP)为
垂直精度衰减因子(VDOP)为
站心坐标系下的定位方程为
式中,几何矩阵
可由i(i＝1,2,…,n)颗卫星的仰角θ(i)、方位角α(i)表示：
站心坐标系下的系数矩阵
与几何矩阵
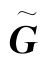的关系为
例7-1 计算由4颗卫星组成的最佳几何分布的各种精度因子值。
代入式(7.31),可得
则各种精度因子为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
