本节主要介绍捷联式惯性导航系统的自主式对准,包括粗对准和精对准两个阶段。在介绍捷联式惯性导航系统粗对准部分,将主要介绍解析粗对准和间接粗对准两种方法。捷联式惯性导航系统精对准是在静基座条件下,在对准过程中不断用新的转换矩阵代替粗对准结束时的转换矩阵,从而使导航计算机计算出的当地地理坐标系与真实当地地理坐标系接近,将误差角减到最小。
6.5.1.1 粗对准
1.解析粗对准
解析粗对准是在静止条件下进行的,假定已知当地纬度L,设b为载体坐标系,规定xb、yb、zb分别指向载体的右、前、上方,n为导航坐标系(当地地理坐标系)规定xn、yn、zn分别指向东、北、天方向,则重力加速度和地球自转角速度在n系的分量是确定已知的,可以表示为
![]()
式中,g——重力加速度幅值;
ωie——地球自转角速度。
解析粗对准就是利用已知的gn、ωnie和传感器测量值gb、ωbie来估计Cnb。由于粗对准时间较短,因此通常采用对传感器测量值取平均的方法来提高对准精度。解析粗对准通常有两种方法计算捷联矩阵:一种是利用g、ωie和构造的g×ωie来计算Cnb;另一种是利用3个相互正交的向量g、g×ωie、(g×ωie)×g来计算Cnb。这两种方法之间除了选取的向量不同外,计算过程均一致,但后一种方法的精度要高于前一种方法。下面对后一种方法利用3个相互正交的向量g、g×ωie、(g×ωie)×g计算Cnb来进行介绍。
根据坐标转换关系,g和ωie在载体坐标系与导航坐标系满足如下关系:
![]()
在自主式初始对准中,载体静止在地面上,忽略载体系统的晃动影响(即不考虑陀螺仪和加速度计的测量误差),有
![]()
式中,ωb,fb——陀螺仪和加速度计的输出。
此时,估计值Cnb为
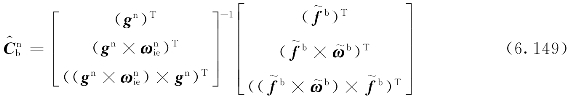
受到传感器的测量误差影响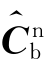 不满足正交性要求,可按下式进行正交化:
不满足正交性要求,可按下式进行正交化:
![]()
式中,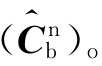 ——正交化后的估计值。
——正交化后的估计值。
2.间接粗对准方法
定义两个坐标系:
(1)初始时刻载体惯性系(b0):与初始对准开始瞬时的载体坐标系重合,随后相对于惯性空间无转动。
(2)初始时刻导航惯性系(n0):与初始对准开始瞬时的导航坐标系(即当地地理坐标系)重合,随后相对于惯性空间无转动。
间接初始对准方法的关键是求解b0系与n0系的方位关系,即Cn0b0。
如图6.6所示,从惯性系中观察地球表面某固定点的重力矢量,在地球自转一周时,该重力矢量随地球自转形成一个锥面,重力矢量的方向为地向,其变化率为东西方向,因此重力矢量及其变化率包含了当地地理坐标系信息。
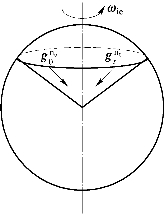
图6.6 惯性空间中重力矢量形成锥面图
在n系内表示重力加速度矢量gn与在n0系内表示重力加速度矢量gn0之间的关系为
![]()
而
![]()
式中,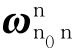 ——n系相对于n0系的转动角速度在n系内的表示。
——n系相对于n0系的转动角速度在n系内的表示。
由于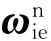 为常值,即n系相对于n0系为定轴转动,因此式(6.152)可解得
为常值,即n系相对于n0系为定轴转动,因此式(6.152)可解得
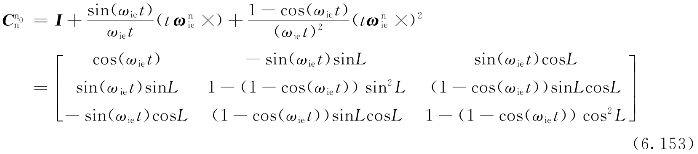
因此,有
![]()
加速度计的比力输出在b0系投影为
![]()
式中,
![]() (https://www.xing528.com)
(https://www.xing528.com)
式中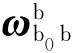 ——b系相对于b0系角速度在b系内的表示;
——b系相对于b0系角速度在b系内的表示;
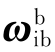 ——陀螺仪测量值;
——陀螺仪测量值;
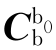 ——可由姿态更新算法求出。
——可由姿态更新算法求出。
加速度测量值与重力矢量有以下关系:
![]()
两边左乘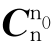 ,得
,得
![]()
即
![]()
式中,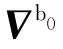 ——b0系内加速度计测量误差及线加速度干扰。
——b0系内加速度计测量误差及线加速度干扰。
理论上,只要获得两个时刻的重力及比力测量值,就可以通过双矢量定姿算法求解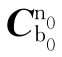 。为了降低线运动干扰影响,使对准精度更高,可以对式(6.159)进行积分处理。如下:
。为了降低线运动干扰影响,使对准精度更高,可以对式(6.159)进行积分处理。如下:
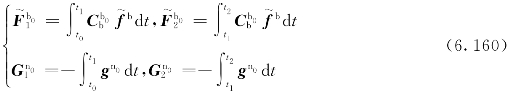
即
![]()
因此,忽略干扰 的影响,可解出
的影响,可解出 ,即
,即
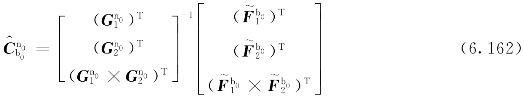
式中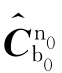 ——初始时刻粗对准的姿态矩阵。粗对准末的姿态矩阵可用下式求解:
——初始时刻粗对准的姿态矩阵。粗对准末的姿态矩阵可用下式求解:
![]()
式中,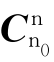 和
和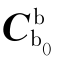 可由式(6.153)和式(6.156)确定。
可由式(6.153)和式(6.156)确定。
6.5.1.2 精对准
精对准的分析根据之前推导的捷联式惯性导航系统的误差方程式,假设粗对准结束后的误差角均为小角度,一般情况下水平误差角比方位误差角小,且静基座条件下载体的真实位置已知且不变,因此系统误差方程可重写为
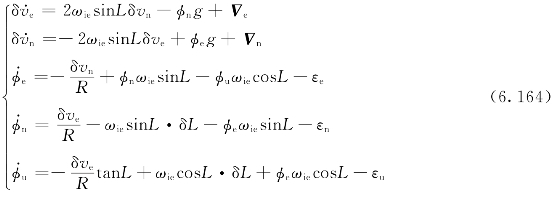
由于初始对准时间短,因此可假定加速度计零偏与陀螺漂移为随机常数,即

因此,捷联式惯性导航系统对准的误差状态方程为
![]()
选取观测量为速度误差δve、δvn,则系统的量测方程为Z=HX+V,进而得状态空间模型为

式中,X——状态变量,X=![]()
W——均值为零的高斯白噪声,W=[wδvewδvnwφewφnwφu0 5×1]T。
其余项为
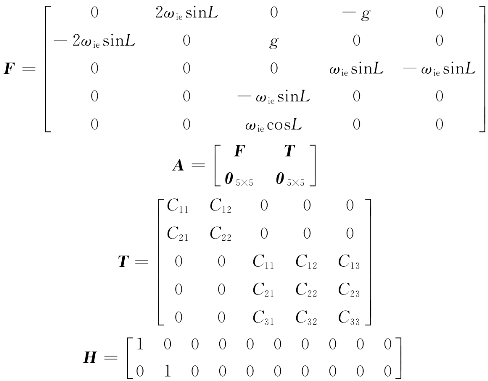
对式(6.167)作离散化处理,可得

式中,一步转移矩阵为
![]()
系统噪声矩阵可用下式求解:
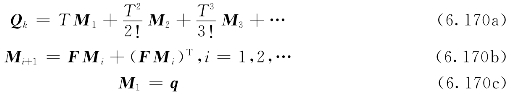
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




