速度更新算法的改进与优化

6.3.2.1　速度计算中的旋转效应和划桨效应分析

以当地地理坐标系作为导航坐标系,将vne简写为vn,并加入时间参数t,式(6.26)写为

设速度的更新周期为T,对式(6.63)在时间段[tm―1,tm]内积分,得

式中——载体在tm和tm―1时刻的速度；

——tm―1时刻的姿态矩阵。

由方向余弦和旋转矢量之间的关系可得,在tm―1≤t≤tm时,有

式中,φ——载体坐标系b从时间tm―1到t的等效旋转矢量；

φ×——φ的反对称矩阵；

φ——φ的模。

对于速度来说,更新周期T＝tm―tm―1较短,φ 非常微小,此时可有如下近似：

其中,

由于(φ×)2为二阶小量,可省略,因此式(6.64)可近似为

将式(6.66)代入式(6.63)得

记为

则式(6.67)可写为

式中,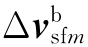——由比力引起的速度补偿量；

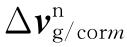——由重力加速度和科氏加速度引起的速度补偿量,又称有害加速度引起的速度补偿量。

1.n有害加速度引起的速度补偿量

由于速度更新时间很短,因此在一个更新周期T内引起的导航坐标系和重力矢量变化都很小,可采用中间时刻的值进行代替。因此,式(6.70)可近似为

式中,tm时刻的导航参数未知,因而tm―1/2时刻的导航参数可采用外推法来计算：

因此,Δvg/corm可以计算得到。

2.Δvsbfm比力引起的速度补偿量

略去表示投影系的上标,式(6.69)可表示为

式中,Δvm——加速度计在[tm―1,tm]时间段内的速度增量,记为

由式(6.66)和式(6.75)可知

对式(6.74)积分项进行如下推导：(www.xing528.com)

由于

将式(6.78)代入式(6.79)的右式,得

将式(6.76)代入式(6.80),得

且当t＝tm时,Δv(tm)＝Δvm,Δθ(tm)＝Δθm,即[tm―1,tm]时间段内的速度增量和角增量；当t＝tm―1时,Δv(tm―1)＝0,Δθ(tm―1)＝0。

将式(6.81)代入式(6.74),有

将式(6.82)右端第二项记为Δvrotm,即

该项称为速度的旋转效应补偿项,是载体的线运动方向在空间旋转引起的,只要载体旋转角速度与加速度不共线,该项总不为零。

将式(6.82)右端第三项记为Δvsculm,即

该项称为速度的划桨效应补偿项,是载体正交轴同频同相的角振动和线振动引起的。

因此,式(6.82)可表示为

6.3.2.2　划桨效应补偿算法

在计算速度的划桨效应补偿项时,由于陀螺仪和加速度计输出的是角增量信号和速度增量信号,因此无法直接按照式(6.84)来计算划桨效应补偿项。为了近似处理,假设陀螺仪角速度和加速度计比力测量均为线性模型,即

式中,a,b,A,B——常值向量。

因此,在一个周期[tm―1,tm]内,角增量Δθ(t)和速度增量Δv(t)为

在速度更新周期T＝tm―tm―1内,对角增量和速度增量进行两次等间隔采样,令由于

因此,有

同理,可得

由式(6.89)和式(6.90),可得

将式(6.86)、式(6.87)、式(6.90)代入式(6.84),可得

将式(6.91)代入式(6.92),得

式中,Δθm(1)和Δθm(2)是[tm―1,tm]内角增量的两个等间隔采样值,Δvm(1)和Δvm(2)是[tm―1,tm]速度增量的两个等间隔采样值,所以该式为划桨效应补偿项的双子样算法。如果对载体的角速度和比力采样抛物线、三次抛物线拟合,就可以得到划桨效应补偿项的三子样算法、四子样算法。

划桨效应补偿项的三子样算法：

式中Δθm(1)、Δθm(2)、Δθm(3)是[tm―1,tm]内角增量的三个等间隔采样值；Δvm(1)、Δvm(2)、Δvm(3)是[tm―1,tm]内速度增量的三个等间隔采样值。

划桨效应补偿项的四子样算法：

式中