常规机械陀螺仪原理及应用

5.1.1.1　概述

牛顿定理、科里奥利定理、刚体的定点转动理论的发展和研究,为机械转子式陀螺仪的产生奠定了坚实的理论基础。机械转子式陀螺仪的基本结构主要包括陀螺转子、陀螺电机、陀螺仪转子轴承、陀螺仪框架轴支承、角度信号传感器、力矩器、测温加温装置、导电装置、壳体等。定轴性和进动性是机械转子式陀螺仪非常重要的特性,这两个特性使得其既具有相对惯性空间保持指向不变的能力,又具有按照要求的规律相对惯性空间转动的能力。

1.定轴性

所谓定轴性,就是当没有任何外力矩作用在高速旋转的陀螺转子上时,不管基座如何转动,陀螺仪的自转轴在惯性空间的指向都保持不变。

2.进动性

自转物体的角动量就是其转动惯量I与其绕同一转轴的角速度ωs的乘积,即

式中,I——构成转子的质量微元与它们到给定转轴距离的平方的乘积的总和。

如图5.1所示,陀螺的转子安装在外部框架的轴承上。轴线ss′穿过轴承中心,轴线tt′和pp′相互正交并穿过转子的质心。图5.1中的圆盘绕ss′轴自转。如果在圆盘上外加一个绕轴线tt′的力偶,那么回盘的自转轴将被迫绕pp′轴旋转。这种旋转运动就是进动。进动轴pp′正交于外加力矩的轴线tt′。

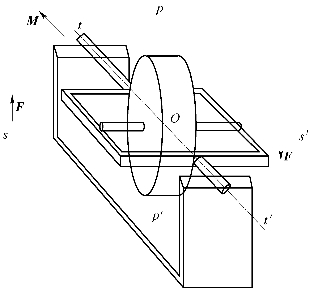
图5.1　进动示意图

如图5.2所示,自转圆盘的角动量为H,以矢量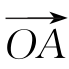表示,即Ha。其中,a为单位矢量。

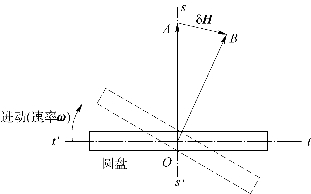
图5.2　进动图解

假设有一个力矩M作用在圆盘上,引起圆盘以速率ω(ω＝ωc,其中c为单位矢量)进动,进动角速度的轴线位于圆盘的平面内,可取为与纸面垂直。过一小段时间之后,圆盘将围绕单位矢量c进动一个角度ωδt,角动量矢量将变为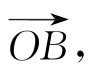即变为(H＋δH)b,其中b＝a＋ωδt(c×a)。

这段时间内角动量的变化用矢量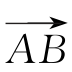表示,使δt→0取极限,角动量的变化率可用下式表示：

由牛顿第二定律可知,角动量的变化率等于加在物体上的力矩M

忽略自转轴方向上的分量,式(5.3)可以写为

这种转子自转轴在外力矩的作用下绕与外力矩相垂直的方向转动的运动,称为进动运动,角速度ω称为陀螺仪的进动角速度。这种在外力矩的作用下产生进动的特殊性能,称为陀螺的进动性。

5.1.1.2　速率积分陀螺仪

单自由度速率积分陀螺仪,在惯性导航和控制应用中提供了空间单轴参考,其结构原理如图5.3所示。其基本结构包括转子、浮筒、力矩器和轴承等。

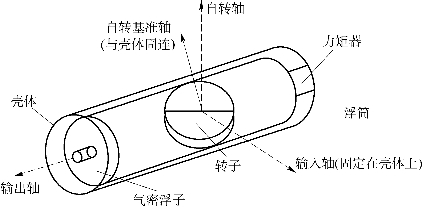
图5.3　单自由度速率积分陀螺仪

工作时,陀螺转子在密封的浮筒内高速旋转,浮筒与壳体之间的小间隙充填了高黏度的液体(浮液)。浮液使得浮筒处于失重状态而不受任何干扰力,还可以提供浮子与壳体之间的黏性阻尼。浮筒通过宝石轴承沿着输出轴架设在壳体中。

当输入角速率时,气密浮子就围绕输出轴产生进动速率,然后在浮液的作用下产生一个围绕输出轴的黏性力矩。这个力矩在输入轴产生进动,进动速率与输入角速率相同,使得转子跟随壳体转动。

假设沿着陀螺仪输入轴(IA)方向的空间角速度为ωIA,那么沿着输出轴(OA)的力矩方程为

式中,JOA——绕输出轴转动惯量；

C——黏度阻尼系数；

H——陀螺角动量；

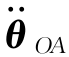
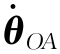——沿输出轴方向的角加速度和角速度。

经过拉普拉斯变换和处理后,可得

式中,τ——时间常数

s——微分算子。

由式(5.6)可知,输入角度和输出角度之间成比例关系。

引起单自由度速率积分陀螺仪漂移误差的主要原因有以下几方面。

(1)与加速度无关的干扰力矩：弹性力矩、电磁干扰力矩、温度梯度引起浮液密度不均匀而产生的力矩、转子轴与浮子轴不正交而产生的交叉干扰力矩。

(2)与加速度一次方有关的干扰力矩：浮子静不平衡力矩、温度变化引起浮子质心位移而产生的不平衡力矩。

(3)与加速度二次方有关的干扰力矩：支承系统不等刚度力矩。

(4)随机干扰力矩：由摩擦力矩、浮子内部结构不稳定、材料蠕变与内应力、浮液中的杂质与气泡及化学分离等因素产生的各种随机干扰力矩。

速率积分陀螺仪提供的测量值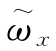可以表达为输入速率真值与下列误差项的总和,即

式中,ωx——陀螺仪绕其输入轴的旋转速率；(www.xing528.com)

ωy,ωz——陀螺仪绕其输出轴和自转轴的旋转速率；

ax,az——陀螺仪沿其输入轴和自转轴的加速度；

Bfx——对加速度无关的零偏；

Bgx,Bgz——对加速度敏感的零偏系数；

Baxz——非等弹性零偏系数；

nx——零均值随机零偏；

Sx——标度因数误差,可以表达为ωx的多项式,以表示标度因数的非线性；

My,Mz——交叉耦合系数。

速率积分陀螺主要误差源的1σ值如表5.1所示。

表5.1　速率积分陀螺主要误差源的1σ值

5.1.1.3　动力调谐陀螺仪

动力调谐陀螺仪利用挠性支承悬挂陀螺转子,并将陀螺转子和驱动电动机分隔开,其挠性支承的弹簧力矩由平衡环产生的动力效应力矩补偿。转子通过一对外扭杆与平衡环连接,平衡环通过一对内扭杆与电动机轴连接。内外扭杆具有很大的抗弯强度和很小的抗扭刚度,所以电动机的驱动力矩可以通过内外扭杆传递给陀螺仪,而转子可以绕着内外扭杆轴线转动,在赤道平面内具有两个旋转自由度,所以动力调谐陀螺仪是一种双自由度陀螺仪。

如图5.4所示,在陀螺仪壳体上安装信号器和力矩器。一轴上的电气对称轴与另一轴上的电气对称轴相互正交,是陀螺仪的测量基准轴。同一轴上的力矩器和信号器的电气对称轴重合。转子镶有径向充磁的磁钢,力矩器的有效工作段线圈镶在转子的环形槽中,并且与环形槽之间留有一定空隙。

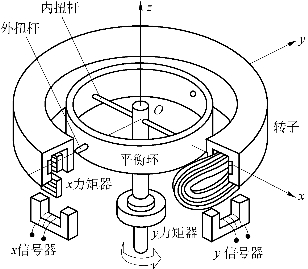
图5.4　动力调谐陀螺仪的典型结构

给x轴力矩器通入施矩电流时,壳体绕x轴转动,自转轴相对壳体出现偏角；x轴传感器输出电压信号,经过放大器放大转换为电流,送给y轴力矩器；y轴力矩器根据电流的大小和极性,产生负向力矩,使转子产生进动。当转子进动角速度和壳体转动角速度相同时,转子偏角达到稳态。在稳态时,转子始终跟随壳体相对惯性空间做同步转动,x轴、y轴上的施矩电流的大小和极性可以分别反映壳体转动的角速度ωx的大小和方向,即

式中,L——陀螺仪的动量矩；

km——y轴力矩器的标度因数；

Iy——控制电流。

有时,用一个品质因数来描述动力调谐陀螺仪的质量。这个品质因数把转子的惯性与框架的惯性联系起来,表达式为

式中,C——转子的自转惯性；

Ig、Jg——框架的横向惯性；

Kg——框架的极惯性。

动力调谐陀螺仪的误差源主要有以下几方面。

(1)对加速度不敏感的零偏：内部产生的杂散磁场、再平衡回路的零偏、杂散磁场与装在转子上的力矩电动机磁铁相互作用、调谐误差、框架阻尼。

(2)对加速度敏感的零偏：转子组件的质量不平衡、扭转组件几何形状的偏差。

(3)非等弹性零偏：原因在于陀螺转子组件在x、y、z方向上的柔性不相等。

(4)非等惯性零偏：原因在于陀螺转子组件在x、y、z方向上的惯性不相同,这项误差对频率敏感。

(5)标度因数误差：由热效应引起。受热导致再平衡系统中所用的磁铁和线圈发生变化。

(6)零均值随机零偏：由误差力矩引起。例如,轴承预加载荷的变化导致自转电机转轴方向的变化,继而产生误差力矩。

陀螺仪所提供的角速率测量值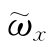和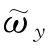,可用数学方法表达如下：

式中,ωx,ωy——陀螺仪绕其输入轴的旋转速率；

ax,ay——沿输入轴的加速度；

az——沿自转轴的加速度；

Bfx,Bfy——对加速度不敏感的零偏系数；

Bgx,Bgy——对加速度敏感的零偏系数；

Baxz,Bayz——非等弹性零偏系数；

nx,ny——零均值随机零偏；

Sx,Sy——标度因数误差；

Mx,My,Mz——交叉耦合系数。

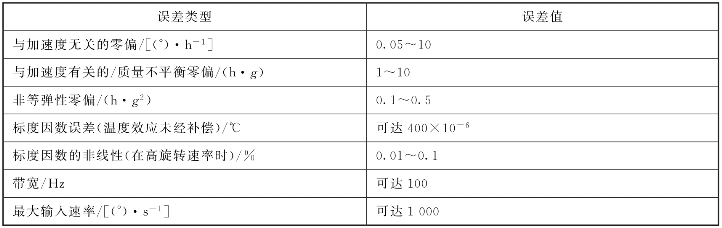
动力调谐陀螺仪主要误差源和性能参数的典型值如表5.2所示。

表5.2　动力调谐陀螺仪主要误差源和性能参数的典型值