粒子滤波的应用与仿真结果

粒子滤波是一种近似贝叶斯滤波的算法,使用参考分布随机产生大量粒子,利用粒子及其权值组成的离散随机测度去近似相关的概率分布,得到系统的估计,并且不断地根据算法更新递推离散随机测度。粒子滤波是一种次优估计框架,当所取粒子数足够大时,可以逼近最优估计。

粒子滤波的缺点：计算量很大,为EKF的若干数量级倍；如果减少粒子数目,则估计精度也会随之下降。

4.8.3.1　粒子滤波算法

标准粒子滤波算法的流程如下：

第1步,初始化。

从先验概率p(x0)中采样N个粒子并初始化权值

第2步,序贯重要性采样(SIS)。

根据蒙特卡洛近似方法,第k次测量时,后验概率密度函数可以由离散采样点按以下方法近似：

p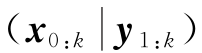是待求的分布,通常采用重要采样方法：假设p(x)为需要近似的概率密度函数,引入重要性密度函数的概率分布与p(x)相同,且容易实现采样,样本即从重点密度采样获得：

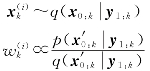
根据贝叶斯递推公式可以表示为下述的递推公式：

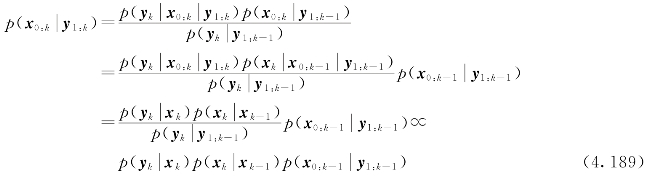
假设重要性密度函数可以分解为

则通过可得样本点x0：k―1,通过可得状态xk,由此可获得新样本x0：k,且权值递推公式为

进一步,如果满足

则重要密度函数只取决于xk―1、yk,则以上式子可简化为

上述过程称为序贯重要采样(Sequential Importance Sampling,SIS),即根据系统每次的量测值递推计算样本及权值。该算法是所有粒子滤波的基础。

第3步,判断是否进行重采样。

粒子滤波存在一个无可避免的退化问题：经过几次递推之后,除了很少几个粒子以外,大部分粒子的权值几乎等于0,从而可以忽略。因此可以采用有效样本个数Neff来度量算法的退化程度：

有效样本越小,说明退化越严重。

第4步,重采样。

重采样的基本思想是淘汰小权值粒子,繁殖大权值粒子。将后验密度离散近似表示为(www.xing528.com)

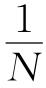重新进行一次采样,生成新粒子集并且满足且新粒子的权值被重新设置为。目前已提出多种重采样方法,如多项式重采样、残差重采样、最小方差重采样、留数采样、系统采样等。

第5步,估计输出。

粒子滤波得到的滤波密度：

滤波估计的均值：

4.8.3.2　应用实例

例4-3对于非线性非高斯系统,有

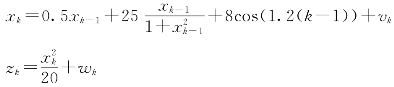
系统过程噪声方差为1,量测噪声方差为1,求基于粒子滤波的系统状态的估计。

解：对于非线性非高斯系统,传统卡尔曼滤波、EKF和UKF均不可以使用,因此采用粒子滤波算法时间系统状态的次优估计。

粒子滤波算法解算过程如下：

(1)参数初始化,即粒子数量Ns、递推迭代次数T、系统噪声方差Q、量测噪声方差R。

(2)初始化样本,即根据先验条件抽取随机初始样本和初始权值1/Ns(i＝1,2,…,Ns)。

(3)For k＝1 to T

由粒子样本代入系统方程,求取随机样本的一次预测样本

将一次预测样本代入量测方程,求得测量的一次预测再结合实际测量zk和重要性密度,求得样本的权值

利用重采样方法对一次预测样本以及权值进行更新,求得更新的粒子样本及权值

End for

(4)利用实现状态估计。

仿真结果：

粒子数Ns＝50时,粒子滤波估计均方根误差为4.188 2,仿真结果如图4.20(a)所示；粒子数Ns＝100时,粒子滤波估计均方根误差为3.212 2,仿真结果如图4.20(b)所示；粒子数Ns＝200时,粒子滤波估计均方根误差为2.716 1,仿真结果如图4.20(c)所示。

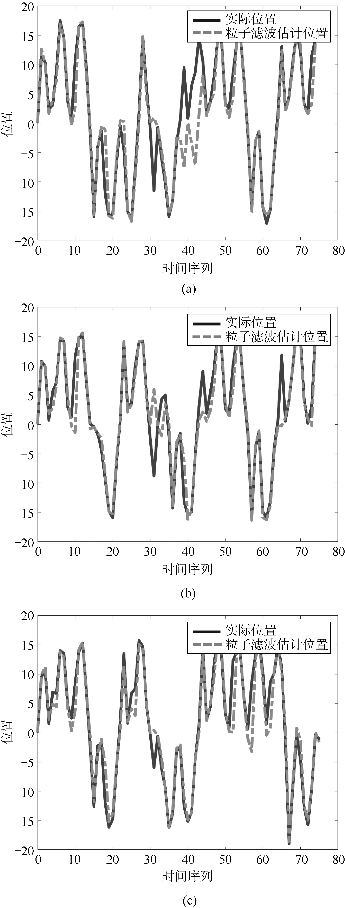
图4.20　粒子滤波仿真结果(书后附彩插)

(a)Ns＝50；(b)Ns＝100；(c)Ns＝200