无迹卡尔曼滤波的优化方法

对于非线性估计问题,传统思路是先对非线性函数进行近似,再进行线性估计,如前文提到的EKF方法。但是对于实际问题中的一些强非线性函数而言,线性化方法不但计算复杂、计算量大,而且不能保证精度。因此,Julier等提出“对概率分布进行近似要比对非线性函数近似容易得多”,从而提出了无迹卡尔曼滤波(Unscented Kalman Filtering,UKF)方法。

接下来,通过一个例子来简单介绍无迹卡尔曼滤波方法。

如图4.16所示,x符合高斯分布,y＝g(x)是非线性函数,通过蒙特卡洛法采样可得y的分布,并将其近似成高斯分布,但是该方法的计算量很大,特别是当维数增加时,采样点个数将呈指数增加。对无迹卡尔曼滤波(UKF)而言,只需选取有限个采样点,然后进行非线性变换,再通过加权统计变换后的结果的分布,如图4.17所示。可以看出,其分布与采用蒙特卡洛法采样得到的分布十分接近。因此,无迹卡尔曼滤波可以在减少采样粒子点数的同时保证逼近精度。

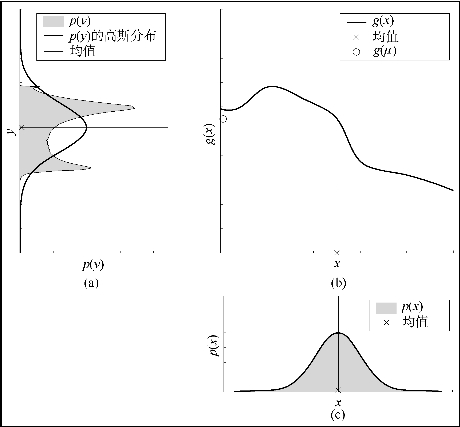
图4.16　蒙特卡洛法采样求取y的分布

(a)p(y)函数；(b)g(x)函数；(c)p(x)函数

因此,简单来说,无迹卡尔曼滤波需要经过3个步骤(图4.18)：首先,利用一定的采样规律从原分布中进行采样；然后,进行非线性变换；最后,对变换结果进行加权统计其分布特性。这一过程被称为UT(Unscented Transformation),它是UKF方法的核心和基础。

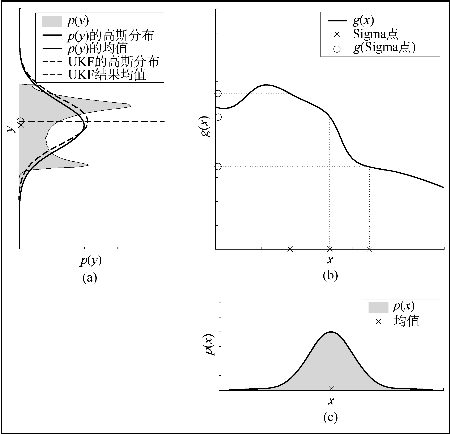
图4.17　UKF法采样求取y的分布

(a)p(y)函数；(b)g(x)函数；(c)p(x)函数

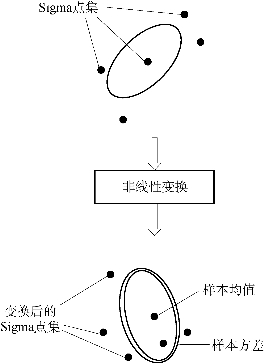
图4.18　UT变换示意

4.8.2.1　UT变换

假设x为n维随机变量,均值为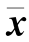,方差为Px,经过非线性变换y＝f(x)进行传递,得到y的统计特性(一般很难精确求解)。UT变换利用加权统计线性回归这一数学原理,计算随机变量的后验分布函数。

第1步,构造Sigma采样点集。采用对称采样策略,对于n维系统,采样点个数为2n＋1,则采样点分别为

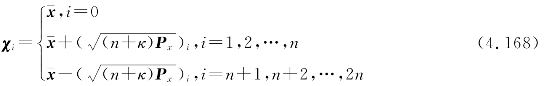
各采样点的一阶统计特性的权系数为Wmi,二阶统计特性的权系数为Wci,且满足

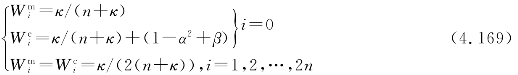
式中,κ——尺度参数,用于控制每个点到均值的距离,调整它可以提高逼近精度,κ＝α2(n＋λ)―n。

要想计算式(4．169),则需要确定参数α、β、λ。其中,α用于确定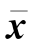周围采样点的分布,通常取一个很小的正数；β为状态分布参数；λ为第2个尺度参数；α、β、λ的具体取值可参考文献[147]。

第2步,将求得的采样点代入函数f(˙)。

y的均值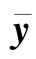和协方差Py可以通过以下公式进行计算：

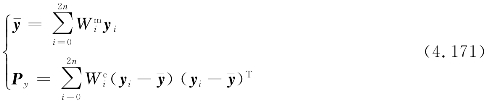
4.8.2.2　UKF算法

假设第k次量测时,非线性系统的状态方程和量测方程为

式中,xk——系统的n维状态量；

yk——系统的p维观测量；

wk——系统的m维过程噪声量；

vk——系统的l维观测噪声量。

vk和wk为互不相关的高斯白噪声,其协方差矩阵分别为Pv、Pw。

在式(4．172)中,过程噪声和测量噪声都隐含在系统内部,因此需要对状态变量进行扩展,定义n＋m＋l维增广状态为

(www.xing528.com)

均值和方差分别为

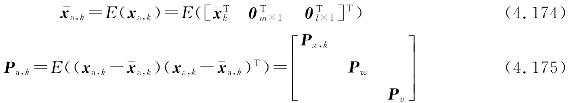
式中,Px,k——状态量xk的协方差矩阵。

下面介绍UKF算法的具体过程。

第1步,初始化。

假设初始状态的均值为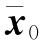,方差为P0,分别为

增广状态初始时刻的均值为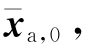,方差为Pa,0,可由式(4．174)、式(4．175)求得。

第2步,定义增广采样点为第k―1次量测时,增广采样点集为

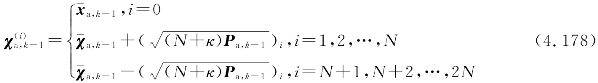
式中,N——增广状态的维数

然后,根据式(4．169)计算权值。

第3步,状态的时间更新。

状态的时间更新是指选定状态的所有采样点,利用UT变换来计算状态的后验均值和方差。由式(4.178)可知第k―1次量测时的采样点集,则第k次量测时,状态量x对应的采样点集的传递过程为

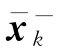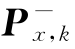状态量x的后验均值和方差为

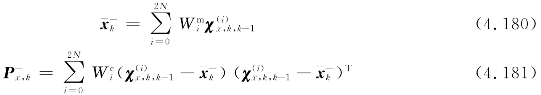
将采样点代入量测方程,记第k次量测时量测均值的预测为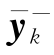,则有

第4步,量测值更新。

本步骤根据4．2节介绍的经典卡尔曼滤波进行量测更新,但是更新方程并不相同。

记第k次量测时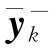的协方差矩阵为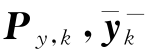与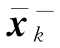之间的协方差矩阵为Pxy,k,则有

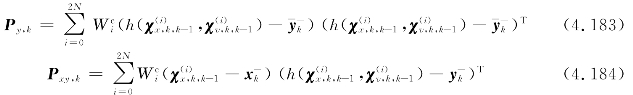
卡尔曼增益K为

状态估计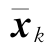及协方差矩阵Px,k分别为

4.8.2.3　应用实例

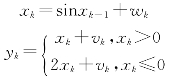
例4-2一维非线性随机系统为其中,系统噪声方差Q＝0.01,量测噪声方差为R＝0.09,利用UKF对状态量进行估计。

解：系统状态初值均值设为0,误差方差设为10,迭代次数为100次,得到的仿真结果如图4.19所示。

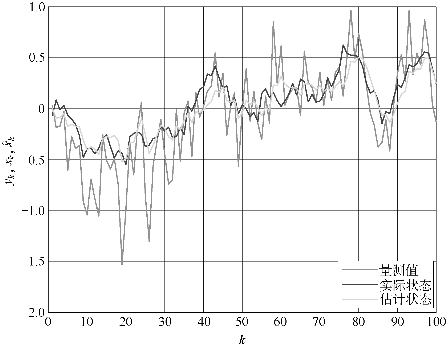
图4.19　UKF仿真结果(书后附彩插)