子滤波器相关的融合算法

假设各子滤波器的状态估计可表示为其中,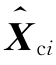是第i个子滤波器对各子滤波器中的公共状态Xc的估计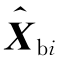则是对第i个子滤波器的特有状态的估计。此时,只需对公共状态的估计进行信息融合。

4.7.2.1　信息分配原则与全局最优估计

联邦滤波器是一种两级滤波结构,如图4.11所示。公共参考系统的输出既提供给主滤波器,又提供给子滤波器,但是子系统的输出只提供给子滤波器,主滤波器参考各子滤波器的状态估计值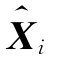和对应的误差协方差阵Pi进行信息融合,得到全局状态估计值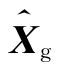和误差协方差阵Pg,这两个量又会反馈给子滤波器。值得注意的是,此时误差协方差阵Pg会被放大倍。而且,在主滤波器中,预测误差的协方差阵也会更新为Pg的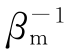倍。βi与βm称为信息分配系数。

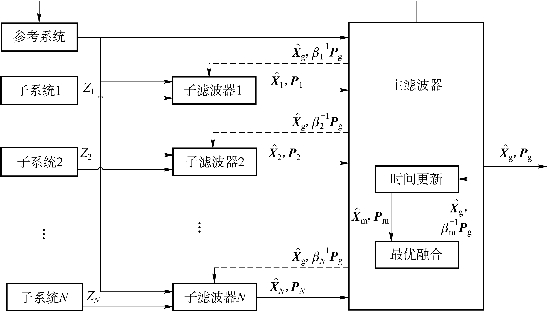
图4.11　联邦滤波器结构

在系统中,状态方程和观测方程的信息可以分别用过程噪声协方差的逆Q―1和观测噪声协方差的逆R―1来表示,状态初值的信息可以用初始状态估计的协方差阵的逆P―10来表示,此时状态方程的信息量可用P―1来表示。并且,公共状态的过程噪声包含在所有子滤波器和主滤波器中,而子系统的观测噪声只包含在对应的观测方程中,因此过程噪声会存在重复计算的问题,而观测噪声不存在此问题。

因此在计算时,将过程噪声信息量Q―1分配到各子滤波器和主滤波器中,即

假设状态估计的信息也按照该方法同样分配,即

并且状态估计初始信息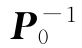也按上述方法分配。

需要注意的是,该方法是建立在各子滤波器的局部估计是不相关的假设下,即Pij＝0(i≠j)。

为了满足该假设,需要对滤波系统建立一个增广系统,它的状态向量是N个子滤波器和主滤波器的状态值,即

式中,Xi——第i个子系统的状态向量是各子滤波器的公有状态,Xbi是第i个子滤波器的专有状态。

容易看出,Xc是增广系统中冗余的状态量。

第k次测量时,增广系统的状态方程为

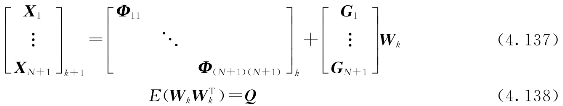
第i个子系统的观测方程为

式中,

增广系统的协方差阵可表示为

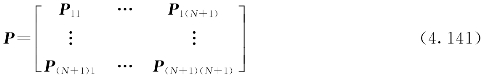
4.7.2.2　联邦滤波的时间更新

由经典卡尔曼滤波的时间更新方程可推得

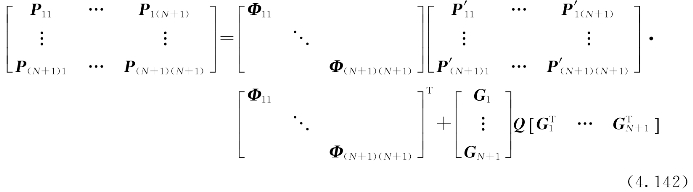
并定义

即

由该式可看出,在时间更新过程中会引入各子滤波器估计的相关。下面对这些相关进行消除。

由矩阵理论可知,(https://www.xing528.com)

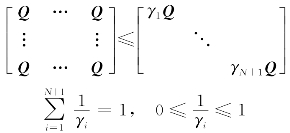
因此,式(4.144)可改写为

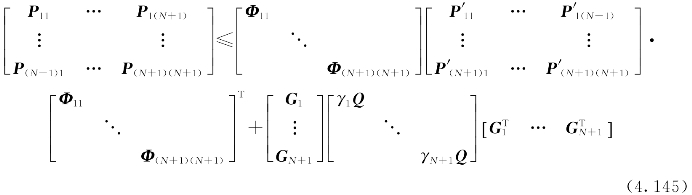
取保守估计的结果,即

式(4.147)说明,此时时间更新是在各子滤波器中独立进行的,子滤波器之间没有相关的运算。只要P′ji＝Pji(k―1)＝0,就可以推导出Pji＝Pji(k,k―1)＝0。即只要初始协方差矩阵非对角线元素Pji(0)＝0,就可以推导出Pji(1,0)＝0,并依次可得Pji(k―1)＝0和Pji(k,k―1)＝0。

按照该方法,将初始方差阵也进行放大,并可以忽略各子滤波器初始方差阵之间的关联项,即

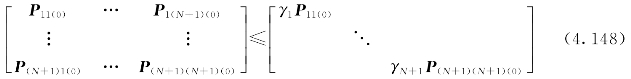
此时,Pji(0)＝0,可推出Pji(1,0)＝0,并依次可推得Pji(k―1)＝0和Pji(k,k―1)＝0。

上述方法得到的各子滤波器的估计是不相关的,但由于该方法对误差协方差阵进行了放大估计,因此此时各子滤波器的估计值不是最优的。并且,有关学者已经证明：局部估计是次优的,但是全局估计的结果是最优的。这是由于第i个滤波子系统的过程噪声方差矩阵Q放大为γiQ,即子滤波器在信息分配过程中只得到总信息量Q―1的γ―1i份,但由于在合成过程中信息量又会恢复到原来的值,所以合成之后的估计是最优的。

4.7.2.3　联邦滤波的观测更新

由上一小节可知,观测更新后的滤波误差方差矩阵Pii被放大了γi倍,则由初始估计误差方差阵Pii(0)和过程噪声方差阵Q被放大了γi倍,可以推得预测误差方差矩阵Pi(k,k―1)和估计误差方差矩阵Pi(k)都被放大了γi倍。

由观测更新方程可得

由式(4.149)可以看出,当Pi(k,k―1)放大γi倍时,Pi(k)并不会放大同等的倍数。因此,在联邦滤波算法中,可以采用全局滤波来对局部滤波值和滤波误差方差阵进行更新,即

更新后的滤波误差方差阵Pi(k)是Pg(k)的γi倍,并且由式(4.138)可推导出一步预测误差方差阵Pi(k＋1,k)也是Pg(k＋1,k)的γi倍,并且容易得到

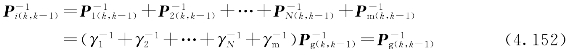
上式中的局部滤波最优误差方差矩阵也可写为

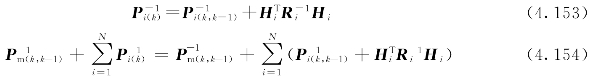
即

从上式可以看出,全局滤波器是利用融合各子滤波器的独立测量信息R―1i来进行最优观测更新的。需要注意的是,如果经过几次局部滤波才进行依次融合,那么全局估计将不是最优的。

根据前面的分析,子滤波器和主滤波器的状态向量都由公共状态Xc和专有状态Xbi(i＝1,2,…,N,m)组成,则子滤波器的协方差矩阵可以表示为

式中,Pcibi,Pbici——公共状态和子系统专有状态的耦合项。

4.7.2.4　联邦滤波器的设计步骤

根据上面的理论分析,对联邦滤波器的设计步骤总结如下：

(1)将子滤波器和主滤波器的初始估计误差方差阵放大γi倍,使子滤波器的初始估计协方差阵互不相关。

(2)将子滤波器和主滤波器的过程噪声方差阵放大γi倍,使子滤波器的过程噪声方差阵互不相关。

(3)对各子滤波器进行观测,获得局部估计值。

(4)得到子滤波器的局部估计和主滤波器的估计后,按照式(4.150)、式(4.151)进行融合。

(5)用全局最优滤波解来更新子滤波器和主滤波器的滤波值、估计误差方差阵。