扩展卡尔曼滤波的应用与优化

4.6.2.1　EKF算法

按照标称状态线性化的卡尔曼滤波方程存在以下问题：在实际情况中不能保证状态偏差ΔXk足够小；解算标称解较困难。因此,可以围绕滤波值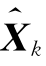将非线性函数f(˙)和h(˙)展开成泰勒级数,并略去二阶(及以上)项来进行线性化的方法,得到非线性系统的线性化模型。围绕滤波值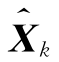进行线性化的滤波方法称为扩展卡尔曼滤波方法。由系统方程(4.91)中的状态方程,将非线性函数f(˙)围绕滤波值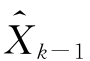展开成泰勒级数,并略去二阶(及以上)项,得

令

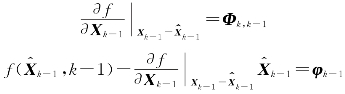
则状态方程为

与卡尔曼滤波基本方程相比,状态方程增加了非随机的外作用项φk―1。

针对式(4.91)中的观测方程,将非线性函数h(˙)围绕滤波值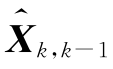展开成泰勒级数,并略去二阶(及以上)项,得

令

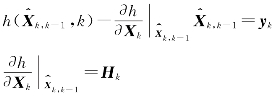
则观测方程为

容易看出,观测方程增加了非随机观测误差项yk。

由4.2.1节给出的离散型卡尔曼滤波的基本方程,可得离散型推广的卡尔曼滤波方程为

即

式中,

即

所以,有(www.xing528.com)

因此,离散型推广的卡尔曼滤波递推方程组为

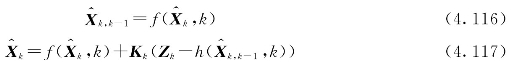
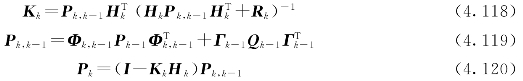
初始值为

式中,

需要指出的是,上述离散型卡尔曼滤波方程只有在滤波误差和一步预测误差都较小的情况下才适用。

EKF方法仍存在以下不足：

(1)由于必须求非线性函数的雅可比矩阵,因此对于模型复杂的系统,求解烦琐且容易出错。

(2)由于引入了线性化误差,因此对于非线性强度高的系统,容易导致滤波效果下降。

4.6.2.2　应用实例

例4-1考虑图4.9所示的例子,空中水平抛射的物体,初始水平速度vx(0)＝500m/s,初始水平位置为x(0)＝0,y(0)＝50m,空气阻力与速度平方成正比,水平和垂直阻尼系数kx＝0.1,ky＝0.5,且水平方向和竖直方向受到的零均值白噪声分别为干扰力δx、δy,方差分别为Rx＝1.5,Ry＝1.5；在原点处有一雷达观测设备,可测得物体距雷达的距离和角度,量测噪声均方差分别为10和0.01。用EKF估计目标位置。

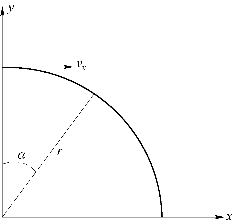
图4.9　EKF实例：空中水平抛射物体

解：系统模型为

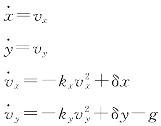
量测方程为

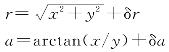
仿真结果如图4.10所示。

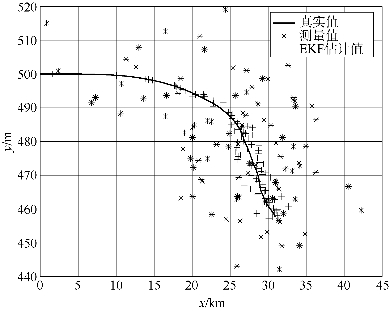
图4.10　EKF估计结果