离散卡尔曼滤波方程及分析详解

4.2.2.1　离散卡尔曼滤波的具体计算

离散卡尔曼方程可以分成两部分：第一部分是式(4.5)、式(4.6),它们是卡尔曼滤波方程；第二部分是式(4.7)～式(4.9),它们称为卡尔曼滤波方程的增益矩阵递推算式。因此,整个卡尔曼滤波的计算也可以分为两部分。

第一部分：卡尔曼滤波方程的计算。卡尔曼滤波方程的计算流程如图4.2所示。

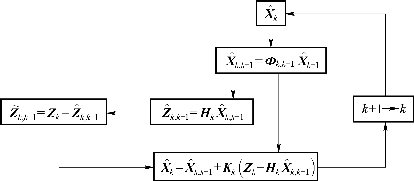
图4.2　卡尔曼滤波方程的计算流程

由于初始时无观测值,因此初始滤波值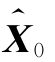可由下式确定：

第二部分：卡尔曼滤波方程的增益矩阵Kk的递推计算。该部分的计算流程如图4.3所示。

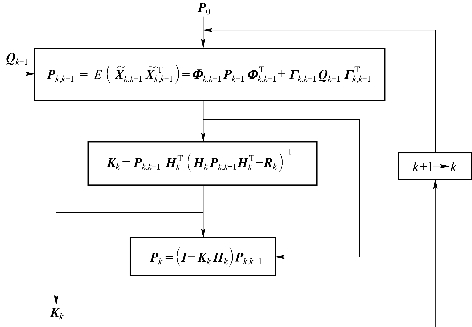
图4.3　卡尔曼滤波方程的增益矩阵递推计算流程

协方差矩阵初值的确定为

(www.xing528.com)

4.2.2.2　离散卡尔曼滤波的特点

离散系统的卡尔曼滤波器是一种线性无偏递推滤波器。线性性质是指状态估计值是观测值的线性函数；无偏性质是指状态估计值与真实值均值相等；递推性质表示任意一次估计值均可利用新的观测值去修正前一次的估计值来得到。递推性质对于在线实时估计是至关重要的。

离散系统的卡尔曼滤波器具有以下特点：

(1)卡尔曼滤波不仅适用于单输入单输出平稳序列的滤波,还适用于马尔可夫序列或高斯―马尔可夫序列的滤波,应用范围十分广泛。

(2)从卡尔曼滤波方程可以看出,其计算过程是一个不断进行“预测―修正”的过程,在求解时不需要存储大量数据,便于实时处理,易于计算机实现。

(3)由式(4.33)可知,滤波增益矩阵Kk与观测值无关,因此可以预先计算得到,以减少实时在线计算量。值得注意的是,在求时,其阶数取决于观测方程的维数m(通常为较小量)。

(4)Pk代表了滤波器的精度指标,其主对角线上的元素就是滤波误差向量各分量的方差,它表明了滤波估计的精度。

(5)增益矩阵Kk与初始误差方差矩阵P0、系统过程噪声方差矩阵Qk―1以及观测噪声方差矩阵Rk之间具有以下关系：

①由式(4.7)、式(4.8)可以看出,P0、Qk―1和Rk(k＝1,2,…)同时乘以一个相同的标量时,Kk值不变。

②由式(4.7)可得,当Rk增大时,Kk将变小。即当观测噪声增大时,观测信息的误差较大,滤波增益Kk就应取小一些,以减弱观测噪声对滤波值的影响。

③当P0和(或)Qk―1变小时,由式(4.8)可以看出,Pk,k―1将变小,而从式(4.9)可以看出,这时的Pk也变小,从而Kk变小。即Pk变小,表示状态估计的初始值具有较高的精度；若Qk―1变小,表示系统过程噪声变小,得到的状态估计值精度变化。于是,增益矩阵应取小一些,以便给予较小的修正。

综上所述,增益矩阵Kk与Qk―1成正比,而与Rk成反比。