离散卡尔曼滤波的数学模型解析

4.2.1.1　随机线性离散系统的数学模型

设离散化后第k时刻的系统状态方程和观测方程分别为

式中,Xk——系统的n维状态向量；

Zk——系统的m维观测向量；

Φk,k―1——n×n维非奇异状态转移矩阵；

Γk,k―1——n×p维系统过程噪声输入矩阵；

Hk——n×n维观测矩阵；

Wk——p维系统随机过程噪声序列；

Vk——m维系统随机观测噪声向量。

而且,关于随机线性离散系统噪声的假设和性质如下：

(1)卡尔曼滤波要求Wk和Vk是互不相关的零均值的白噪声序列,即

式中,Qk,Rk——Wk和Vk的方差矩阵,且Qk为对称非负定矩阵、Rk为对称正定矩阵；

δkj——克罗内克符号,其定义为

(2)系统的初始状态X0是某种已知分布的随机向量,其均值向量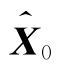和方差矩阵P0为

Wk、Vk与初始状态X0不相关。

4.2.1.2　随机线性离散系统的卡尔曼基本方程

随机线性离散系统的方程为式(4.1),且满足提出的各种假设,已获得在第k―1时刻Xk―1的最优估计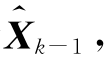,则对于在k时刻Xk的估计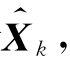,可按以下滤波方程求解：

状态预测：

状态估计：

滤波增益矩阵：

最优预测估计误差方差阵：

估计误差方差矩阵：

上述5式即随机线性离散卡尔曼滤波基本方程。只要给定初值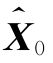和P0,则根据在k时刻的观测值Zk,就可以递推计算得到在k时刻的状态估计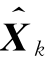(k＝1,2,…)。

4.2.1.3　随机线性离散卡尔曼滤波方程的直观推导

假如在k时刻已经得到观测值Z1,Z2,…,Zk,且找到了Xk―1的一个最优线性估计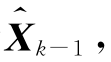即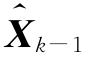是Z1,Z2,…,Zk的线性函数,那么如何得到在k时刻对状态量的估计值呢?简单看来,可用式(4.5)作为Xk的预测估计。由于Vk为零均值的白噪声,因此在k时刻对系统观测值的预测估计为为状态预测估计。当在k时刻获得观测值Zk时,它与预测估计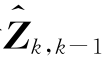之间有一定误差,将该误差定义为

在一般情况下,状态预测估计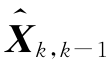与观测值Zk都可能有误差,为了得到在k时刻Xk的滤波值,可以利用预测误差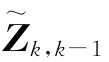来修正原来的状态预测估计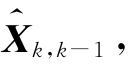,于是有

式中,Kk——待定的滤波增益矩阵。

同时,记获得观测值Zk前后对Xk的估计误差：

接下来要解决的问题是如何通过使目标函数最小来确定最优滤波增益矩阵Kk。

由式(4.1)、式(4.11)、式(4.12)可推得

又因为(www.xing528.com)

由于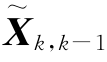是Z1,Z2,…,Zk―1的线性函数,故有

因此,滤波误差方差矩阵为

对式(4.16)做如下变换：

则可推得

该式前两项不含Kk因子,因此为使滤波误差方差矩阵Pk极小,应满足以下条件：

即

此时,误差方差矩阵Pk为

一步预测误差方差矩阵Pk,k―1为

Xk的状态预测估计误差可以表示为

根据式(4.1),进一步推得一步预测方程为

以上为离散卡尔曼方程的全部推导过程。

4.2.1.4　离散卡尔曼滤波方程的正交投影法推导

在第3章介绍线性最小方差估计时,曾引出过正交投影的概念。该概念是正交投影法推导的理论基础。

根据前k―1次的观测值得到的对Xk―1的线性最小方差估计值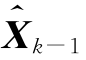为

则一步预测状态量为

由于过程噪声方差矩阵和测量向量不相关,所以式(4.27)可进一步写为

同样,根据前k-1次的观测值得到的对Zk的线性最小方差估计值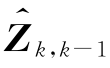为

将式(4.28)代入,可得

根据定义容易发现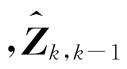是Zk在Zk―1上的正交投影向量。

下面进一步推导对状态量Xk的最优估计值。

根据式(4.26),可以写出

进一步展开,可得

根据更新信息定理,可以得到

并记

式中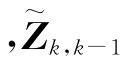——第k次观测量Zk的预测误差,由于它包含了第k次量测量Zk的信息,因此被称为“新息”。并且有

将式(4.31)、式(4.32)代入式(4.30),可得

令

则可得

其余方程的推导与直观推导的过程一致,不再赘述。