最小方差估计方法

当估计误差的方差阵达到最小时,求得的估计值称为最小方差估计。该方法需要知道被估随机变量的概率密度函数和数学期望。

假设X与Z之间的关系为Z＝Z(X)＋V,由于V是随机误差,因此X无法从Z的函数关系式中直接求取,而必须按统计意义的最优标准求取,其指标可表示为

在此省略推导过程,直接给出结论如下：

(1)随机向量X的最小方差估计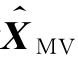(Z)是在观测向量为Z的条件下,X的条件数学期望,即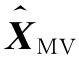(Z)＝E(X|Z)。

(2)最小方差估计是X的无偏估计,即E(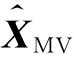(Z))＝E(X)。

(3)由于最小方差估计是无偏估计,所以估计的均方误差阵就是估计误差的方差阵,即

(4)若被估计向量和量测向量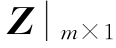都服从正态分布,且

则X的最小方差估计为

估计的均方误差为即满足正态分布的随机向量的最小方差估计,知道估计向量X和量测向量Z的一阶、二阶矩阵即可求得。

如果估计量和量测量存在以下线性关系：(www.xing528.com)

则可以进一步简化。

假定：E(V)＝0,Var(V)＝CV,E(X)＝mX,Var(X)＝CX,且X和V互不相关,则

或写为

例3-3设X为服从正态分布的随机量均值为mX方差为CX对X用m台仪器同时直接测量,测量误差都是服从正态分布的随机变量,均值为零,方差为CV,求X的最小方差估计和该估计的均方差。

解：根据题意,量测方程为

根据式(3.8),该状态量的最小方差估计为

该估计的方差为

无偏估计的误差均方差表示误差分布在0附近的密集程度,所以误差均方差也描述估计的精度质量。误差均方差越小,估计精度就越高。从上述结果可以看出,m越大(即测量仪器越多),估计精度就越高；CX、CV的值越小,估计误差的均方差就越小,这在直观上也易于理解。