最小二乘估计：理论与应用

最小二乘法是高斯(Gauss)在1795年提出的参数估计算法。相较于其他估计法则,该方法十分简单,不需要知道被估计量及量测值的任何统计信息。因此,当不知道X和Z的概率分布密度,也不知道它们的一、二阶矩时,就只能采用该方法进行估计。最小二乘估计以残差(估计量测值与实际量测值)的平方和为最小作为估计准则。

假设第i次测量X和Z之间的关系为

则指标函数为

即

在此省略具体推导过程,直接给出估计量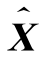的结论：

式中,R＝Var(V)。

使指标函数为最小的充分条件为

从式(3.5)中可以看出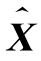是观测数据Z的线性函数,即最小二乘估计是线性估计。(https://www.xing528.com)

当观测噪声的均值为0时,E(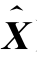)＝E(X),因此最小二乘估计是无偏估计。

高斯利用最小二乘法解决了天文学上的定轨问题,随后又有科学家提出了最小二乘法的其他形式,如加权最小二乘法、递推最小二乘法等。最小二乘法在实际中得到了广泛应用。

但是,最小二乘法有它本身的局限性,它没有考虑被估计参数和观测数据的统计特性,其最优指标只保证了量测的估计均方误差之和最小,而不能确保被估计量的估计误差达到最佳,所以最小二乘法不是一种最优估计方法。此外,这种估计方法在实时计算中需要把所有观测数据储存起来进行统一处理,因此计算量很大。

例3-1为精密测定3种电容器的电容x1、x2、x3,进行了等权、独立、无系统误差的测量,测量结果为1号电容值y1＝0.3,2号电容值y2＝―0.4,1号和3号并联电容值y3＝0.5,2号和3号并联电容值y4＝―0.3。试用最小二乘法求x1、x2、x3的最优估计。

解：列出观测量与被估计量的函数关系：

根据最小二乘法的结论,可得

其中,