【摘要】：本节将对这些最优估计准则进行介绍。估计理论是许多信息融合算法的基本理论。那么,估计问题就是在时间区间[t0,t1]内对X进行观测,在得到观测数据Z＝{Z(τ),t0≤τ≤t1}以后,构造一个观测数据的函数去估计X,称是X的一个估计量,或称X的估计为。并且,当是Z的线性函数时,为线性估计。当需要观测的状态值为X时,这成为预测(外推)问题；当需要观测的状态值为X时,这成为平滑(内插)问题。
组合导航系统中的信息融合技术在估计状态量时,需要利用一定的最优估计准则。估计准则就是用于衡量估计值接近于实际值的程度,常用的估计准则有最小二乘准则、最小方差准则、线性最小方差准则、极大似然准则、极大验后准则等。当估计准则确定后,估计值在某种统计意义上达到最优时,即最优估计。因此,最优估计是针对某一估计准则而言的,即最优估计不唯一。本节将对这些最优估计准则进行介绍。
估计理论是许多信息融合算法的基本理论。假设被估计量X(t)是一个n维向量,而m维向量Z(t)是其观测量,并且观测量与被估计量之间具有如下关系：
式中,h(˙)——已知的m维向量函数,由观测方法决定；
V(t)——观测误差,通常为一个随机过程。(www.xing528.com)
那么,估计问题就是在时间区间[t0,t1]内对X(t)(t＝t1)进行观测,在得到观测数据Z＝{Z(τ),t0≤τ≤t1}以后,构造一个观测数据的函数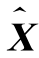
(t)去估计X(t),称
是X(t)的一个估计量,或称X(t)的估计为
。并且,当
是Z的线性函数时,为线性估计。
当需要观测的状态值为X(t)(t＞t1)时,这成为预测(外推)问题；当需要观测的状态值为X(t)(t＜t1)时,这成为平滑(内插)问题。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
