欧拉角法：坐标系变换的最直观表示方法

2.3.2.1　欧拉角的定义

从一个坐标系到另一个坐标系的变换可以通过依次绕不同坐标轴的3次连续转动来定义,欧拉角法是表示这三次转动的最直观的方法,尤其是在表示载体坐标系与导航坐标系之间的变换时。3次转动可以用数学方法表述成3个独立的方向余弦矩阵。从参考坐标系到载体坐标系的变换过程如图2.12所示。

图2.12　从参考坐标系到载体坐标系的变换过程

绕―z轴转动ψ角(偏航角),有

绕x轴转动θ角(俯仰角),有

绕y轴转动γ角(滚转角),有

因此,从参考坐标系R到载体坐标系b的变换矩阵可以由下式给出：

需要注意的是,在使用欧拉角法时,旋转次序不能改变,即欧拉角旋转不具有互换性。(www.xing528.com)

在分析问题时,常对很小的时间段内的运动进行解算,此时可以认为载体的转动角度都很小,因此有

忽略小角度的转动,则通过欧拉角转动所表示的方向余弦矩阵可近似简化为斜对称阵形式,即

该矩阵可以用于表示估计的方向余弦矩阵的误差,以及用于表示姿态连续更新之间发生的微小变化。

2.3.2.2　欧拉角微分方程

载体坐标系b相对于参考坐标系R的转动角速度在载体坐标系b下的投影可表示为

它和三个欧拉角的角速度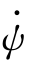˙的关系为

式(2.34)可以整理成如下分量形式：

式(2.35)可在捷联系统中进行解算,用来更新载体相对于所选参考坐标系的欧拉转动。然而,当θ＝±90°时,欧拉角的变换存在奇异值,所以该式的使用会受到限制。因此,在姿态解算的过程中很少使用欧拉角。