利用方向余弦求解问题

2.3.1.1　方向余弦矩阵的定义

图2.11　坐标系示意

如图2.11所示,假设OxRyRzR为任意参考坐标系,沿各坐标轴单位矢量为iR、jR、kR；Oxbybzb为刚体固联坐标系,沿各坐标轴单位矢量为ib、jb、kb,则ib、jb、kb与iR、jR、kR之间的关系可以表示为

其用矩阵形式表示为

假设三维向量V在Oxbybzb坐标系中表示为V＝xbib＋ybjb＋zbkb,在OxRyRzR坐标系中表示为V＝xRiR＋yRjR＋zRkR,则

将式(2.16)代入式(2.17),可得

即

令

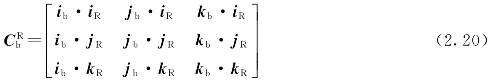
即CRb为从b系到R系的坐标变换矩阵。在式(2.20)中,iR、jR、kRib、jb、kb均为单位矢量。所以CRb中的各项即相应坐标轴之间夹角的余弦值。CRb中的各项元素的计算方式如表2.4所示。

表2.4　CRb中的各项元素

(www.xing528.com)

所以,CRb又称为方向余弦矩阵。

根据定义可得,方向余弦矩阵具有以下性质：

(1)CRb的列向量是b系中的单位矢量在R系中的投影。

(2)CRb＝(CbR)T。

(3)方向余弦矩阵是单位正交矩阵。

(4)根据方向余弦矩阵的正交性可得：

在方向余弦矩阵中,有9个元素、6个约束方程,只含有3个独立变量。

2.3.1.2　方向余弦矩阵微分方程

假设t时刻,由动坐标系b至参考坐标系R的方向余弦矩阵为CRb(t),设坐标系b在Δt时间间隔内相对坐标系R向前旋转小角度矢量,分别绕x、y、z轴转动Δθ、Δγ、Δψ(当时间间隔Δt很小时,转动次序变得不重要),则在t＋Δt时刻的变换矩阵为CRb(t＋Δt),即CRb(t＋Δt)＝CRb(t)A(t),其中A(t)表示b系从t＋Δt时刻到t时刻的方向余弦矩阵。根据2.3.1.1节提出的方向余弦矩阵的推导过程,并且利用小角度原理,可以得到

下面对CRb求导：

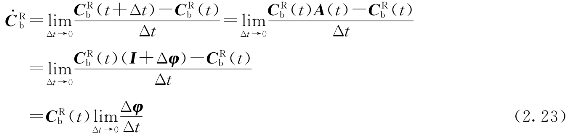
在Δt趋近于0时,Δφ/Δt是载体坐标系相对参考坐标系的转动角速率在载体坐标系中的矢量ωbRb＝[ωxωyωz]T的斜对称矩阵形式,即

可得

式(2.25)可以在捷联式惯性导航系统的计算机中进行解算,以跟踪载体相对于参考坐标系的姿态。