测量系统动态特性优化方法

由前面的分析可知，一阶系统的特性参数是时间常数τ，二阶系统的特性参数是固有角频率ω0与阻尼比ξ。知道这些特性参数的值，就可以建立系统的数学模型，再通过适当的数学运算，就可以计算出系统对任一输入信号的输出响应。尽管这些特性参数取决于系统本身的固有特性，可以有理论设定，但最终必须由实验测定，称动态标定。为了便于统一比较和容易获取，标定时通常选定两种输入形式的输入信号，即正弦信号和阶跃信号，相应地，测定动态特性的表述也有两种形式，即时域阶跃响应特性和频域频率特性。

（1）测量系统的时域特性

以阶跃信号激励为例，分析一阶和二阶传感器的动态特性。

1）一阶测量系统的时域特性。

设一阶测量系统的传递函数为

当输入一个单位阶跃信号时，系统的输出信号为

相应的响应曲线如图1-5所示。由图可见，一阶测量系统存在惯性，阶跃响应不能立即复现输入的阶跃信号，而是从零开始按指数规律上升，输出信号初始上升斜率为1/τ。显然时间常数τ是衡量一阶测量系统动态响应速度的重要参数，τ越小，响应速度越快，也即测量系统的惯性越小。

根据测量系统的输出特性曲线，可以选择以下几个特征时间点作为动态性能指标。

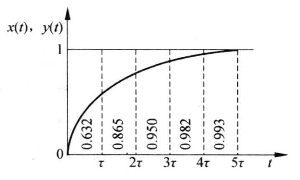
图1-5　单位阶跃响应曲线

时间常数τ：输出y（t）由零上升到稳态值ys的63%所需的时间。

调节时间ts：输出y（t）由零上升到并保持在与稳态值ys的偏差的绝对值在±2%或±5%的范围内所需的时间。

延迟时间td：输出y（t）由零上升到并保持在稳态值ys的一半所需的时间。

•上升时间tr：输出y（t）由10%ys上升到90%ys所需的时间。

对于一阶测量系统，时间常数是非常重要的性能指标，显然时间常数越大，系统到达稳态的时间就越长，其动态性能就越差。因此，应尽可能减小时间常数，以减小系统的动态误差。

2）二阶测量系统的时域特性。

设二阶测量系统的传递函数为

当输入为单位阶跃函数时，系统的输出与固有角频率ω0及阻尼比ξ密切相关。固有频率ω0由系统结构参数决定，ω0越大，测量系统响应速度越快；当ω0为常数时，系统响应速度取决于阻尼比ξ。图1-6为二阶测量系统的单位阶跃响应曲线，阻尼比直接影响系统输出信号的振荡次数及超调量。ξ=0时，为临界阻尼，超调量为100%，产生等幅振荡；ξ＞1时，为过阻尼，无超调，也无振荡，但达到稳态输出所需的时间比较长；ξ＜1时，为欠阻尼，产生衰减振荡，输出达到稳态值所需的时间随ξ的增加而减小；ξ=1时，达稳态输出所需的时间最短。工程中通常取ξ=0.6～0.8，此时最大超调量为2.5%～10%，其稳态响应时间也较短。

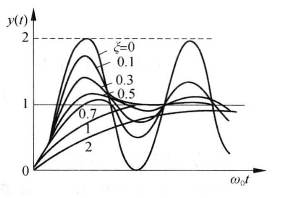
图1-6　二阶系统的阶跃响应曲线

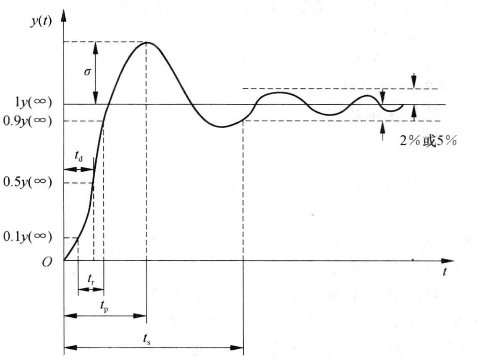
图1-7为表示二阶测量系统性能指标的单位阶跃响应曲线，二阶系统的主要性能指标如下。

(www.xing528.com)

图1-7　表示二阶测量系统性能指标的单位阶跃响应曲线

•上升时间tr。

•延迟时间td。

•峰值时间tp：响应曲线达到超调量的第一个峰值所需要的时间。

•调节时间ts：响应曲线达到并永远保持在一个允许误差范围内所需的最短时间。用稳态值的百分数（通常取5%或2%）做误差范围。

•超调量σ：输出响应的最大偏离量y（tp）与终值y（∞）之差的百分比，即

式中，y（tp）为输出的最大值；y（∞）为输出的稳态值。

上升时间和峰值时间用来评价系统的响应速度；调节时间是同时反映响应速度和阻尼程度的综合性指标；而超调量则是评价系统的阻尼程度。

（2）测量系统的频域特性

当系统输入的激励信号为正弦信号时，则按系统的频率响应特性研究其动态特性。

1）一阶系统的频域响应。

一阶系统频域响应特性曲线如图1-8所示。

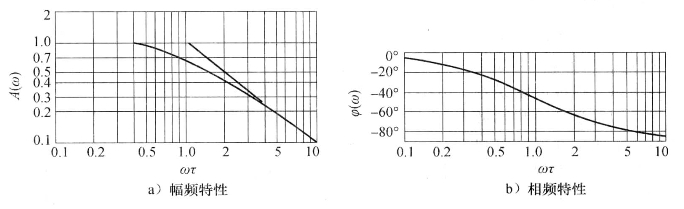
图1-8　一阶系统频率响应特性

由此可见，时间常数τ越小，频率响应特性越好；当ωτ＜＜1时，A（ω）≈1，φ（ω）≈0，表示系统输出与输入呈线性关系，且位差很小，输出能真实反映输入的变化规律。

2）二阶系统的频域响应。

二阶系统频率响应特性曲线如图1-9所示，二阶测量系统频率响应特性的好坏主要取决于系统的固有频率ω0和阻尼比ξ：ξ＜1、ω0＞＞ω时，A（ω）≈1、φ（ω）很小，幅频特性平直，输出与输入呈线性关系，此时测量系统的输出能真实再现输入信号。通常设计测量系统时，使其阻尼比ξ＜1，固有频率ω0至少应大于被测信号频率ω的3～5倍。若被测信号为多频谐波信号时，系统的固有频率理论上应高于输入信号谐波中最高频率ωmax的3～5倍；考虑到在整个频谱内，频率越高，幅值越小，灵敏度越低，因而固有频率的选择应根据测量需要综合考虑。

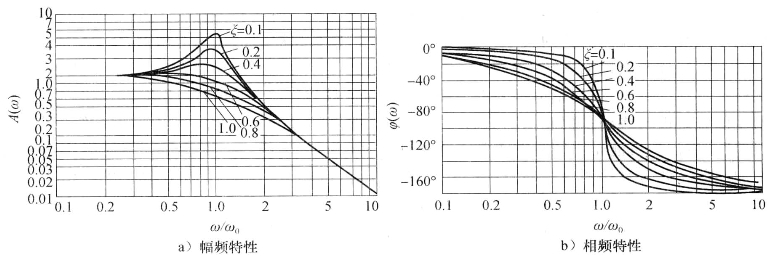
图1-9　二阶测量系统频率响应特性曲线

3）频域特性指标。

衡量测量系统对正弦信号激励响应的频域特性指标主要如下。

•通频带：是系统输出量保持在一定值（幅频特性曲线上相对与幅值衰减3dB）内所对应的频率范围。

•工作频带：系统输出幅值误差为±5%（或±10%）时所对应的频率范围。

•相对误差：在工作频带范围内输出量的相位偏差应小于5°（或10°）。