轮系在各种机械中的应用十分广泛，其功用可概括为以下几个方面

轮系在各种机械中的应用十分广泛，其功用可概括为以下几个方面。

例7.5　实现大传动比传动的轮系分析。

当两轴之间需要较大的传动比时，如果仅用一对齿轮传动，必然使两轮的尺寸差距过大，如图7.13中虚线所示。这样将使传动机构的外廊尺寸庞大，所以两轴间需要较大的传动比时，就可以利用定轴轮系的多级传动来实现，如图7.13中实线所示，这样便可克服上述缺点。

图7.13　实现大传动比的定轴轮系

图7.14　大传动比行星轮系

为了获得大的传动比，也可以采用周转轮系或复合轮系。如图7.14所示的行星轮系中，若各轮的齿数分别为z1=100，z2=101，z2′=100，z3=99，则输入构件H对输出构件1的传动比iH1=10000。可见，根据需要，行星轮系可获得很大的传动比。

例7.6　实现换向传动的轮系分析。

在主轴转向不变的条件下，利用轮系可改变从动轴的转向。如图7.15所示为车床上走刀丝杆的三星轮换向机构。齿轮2、3铰接在刚性构件a上，构件a可绕轮4的轴线回转。如图7.15（a）所示位置，主动轮1的运动经中间轮2及3传给从动轮4，从动轮4与主动轮1转向相反；如转动构件a，使其处于图7.15（b）所示的位置，则齿轮2不参与传动，这时主动轮的运动就只经过中间轮3而传给从动轮4，故从动轮与主动轮1的转向相同。

图7.15　走刀丝杆的三星轮换向机构

例7.7　实现变速传动的轮系分析。

如图7.16所示的轮系中，轴Ⅰ和Ⅱ分别为主动轴和从动轴，齿轮1′与2′固定在轴Ⅰ上，齿轮1与2为双联齿轮，与轴Ⅱ用导向键相连，可在轴Ⅱ上滑动。当操纵控制手柄使双联滑移齿轮分别形成1′与1或2′与2啮合时，就可得到两种不同的传动比。

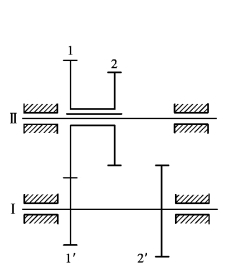
图7.16　定轴轮系变速传动

图7.17　周转轮系变速传动

变速传动也可利用周转轮系来实现，周转轮系变速器如图7.17所示。通过制动器A、B固定不同的中心轮3、6而得到轮系不同的传动比，从而在主动轮转速不变的条件下，可使从动轴H得到两种不同的转速。与定轴轮系变速器比较，周转轮系变速器较复杂，但操纵方便，可在运动中变速。

例7.8　实现结构紧凑的大功率传动的轮系分析。

用作动力传动的周转轮系通常都采用具有多个行星轮的结构，如图7.18所示。各行星轮均匀分布在中心轮的四周，这样，载荷由多对齿轮承受，以减小齿轮尺寸。同时又可使各个啮合处的径向分力和行星轮公转所产生的离心惯性力各自得以平衡，以减小主轴承内的作用力，增加运转的平稳性，实现大功率传动。

例7.9　实现较远距离传动的轮系分析。

主动轮和从动轮间的距离较远时，如果仅用一对齿轮来传动，如图7.19中双点画线所示，齿轮的尺寸就很大，即占空间，又费材料，而且制造、安装都不方便。若改用轮系来传动，如图7.19中单点画线所示，则可以大大改善上述缺点。(www.xing528.com)

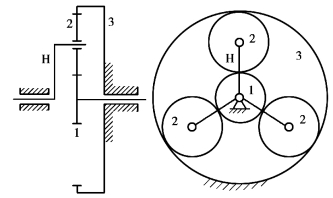
图7.18　大功率传动的周转轮系

图7.19　相距较远的两轴传动

例7.10　实现分路传动的轮系分析。

当输入轴的转速一定时，利用轮系可将输入轴的一种转速运动同时传到几根输出轴上，获得所需的各种转速。如图7.20为滚齿机上实现轮坯与滚刀范成运动的传动简图，轴I的运动经过圆锥齿轮1、2传给滚刀，经齿轮3、4、5、6、7和蜗杆8、9传给轮坯。

图7.20　分路传动

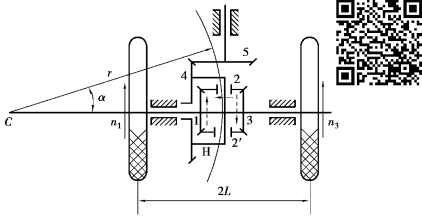
图7.21　汽车后桥差速器

例7.11　实现运动的合成与分解的轮系分析。

由于差动轮系有两个自由度，利用差动轮系的这一特性，不仅能将两个独立的运动合成为一个运动，而且可以将一个主动构件的运动按所需的可变比例分解为两个从动构件的不同运动。如图7.21所示为装在汽车上的差动轮系（常称差速器）。发动机通过传动轴驱动齿轮5，齿轮4与齿轮5啮合并在齿轮4上固连着行星架H，其上装有行星轮2、齿轮1、2、3及行星架H组成一差动轮系。

在该轮系中，z1=z3，nH=n4，故根据式（7.3），有

故

由于左、右两车轮分别与轴1、3固联，因此当汽车直线行驶时两个车轮所走过的路程相同，即要求齿轮1、3转速相等，n1=n3=n4，即齿轮1、2、3和行星架H之间没有相对运动，整个差动轮系相当于同齿轮4固联成一个整体，随齿轮4一起转动，此时行星轮2相对于行星架没有转动。

当汽车转弯时，由于左右两车轮行驶的路程不相等，所以轮1和轮3的转速不同。由于路面摩擦力的作用，当车轮在路面上做纯滚动使汽车向左转弯时，处于弯道内侧的左车轮走的是一个小圆弧，而处于弯道外侧的右车轮走的是一个大圆弧，即要求两车轮所走的路程不相等，因此要求齿轮1、3具有不同的转速。设两车轮中心距为2L，弯道平均半径为r，由于两车轮的转速应与弯道半径成正比，故由图可得

联立解式（7.4）、式（7.5），可求得此时汽车两车轮的转速分别为

此时行星轮除随H一起公转外，还绕其自身轴线自转。公转转速n4通过差动轮系分解成n1和n3两个不同的转速，转速的大小随弯道半径的不同而改变。