周转轮系传动比计算方法优化

通过对周转轮系和定轴轮系的观察和比较就会发现，它们之间的根本差别就在于周转轮系中有转动的行星架，从而使得行星轮既有自转又有公转。由于这个差别，周转轮系的传动比不能直接用定轴轮系传动比的做法来计算。如何能够解决这个问题呢？如果以行星架为参照系，这样就可发现，行星轮只有自转而没有公转，整个周转轮系演化成了定轴轮系。

实际处理的方法称为“反转法”，即给整个周转轮系加上一个大小与行星架转速相等，但方向相反的公共转速“-nH”，使之绕行星架的固定轴线回转，这时各构件之间的相对运动仍保持不变，而行星架的转速变为nH-nH=0，行星架“静止不动”了。这种转化所得的假想的定轴轮系称为原周转轮系的转化轮系。于是周转轮系的问题就可以用定轴轮系的方法来解决了。

下面以图7.11（a）为例，通过转化轮系传动比的计算，得出周转轮系中各个构件之间转速的关系，进而求得该周转轮系的传动比。当对整个周转轮系加上一个公共转速“-nH”以后，周转轮系演化成图7.11（b）所示的转化轮系，各构件的转速的变化如表7.1所示。

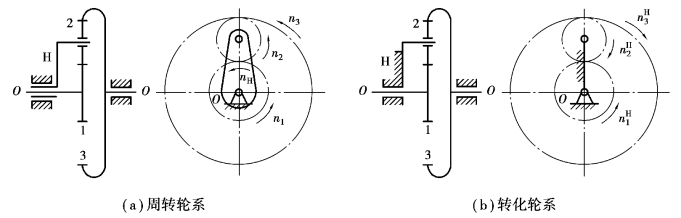
图7.11　周转轮系及其转化轮系

表7.1　周转轮系和转化轮系的转速

在表7.1中，转化轮系中各构件的转速的右上角都带有上标H，表示这些转速是各构件对行星架的相对转速。因为，所以该周转轮系已经转化为定轴轮系，即该周转轮系的转化轮系。三个齿轮相对于行星架H的转速即为它们在转化轮系中的转速，于是转化轮系的传动比可计算如下：

式（7.2）中齿数比前的负号表示在转化轮系中齿轮1与齿轮3的转向相反，即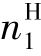与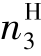的方向相反。应注意区分i13和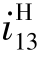，前者是两轮真实的传动比，而后者是假想的转化轮系中两轮的传动比。

根据上述原理，不难得出计算周转轮系的一般关系式。设周转轮系中的两个齿轮分别为G、K，行星架为H，则其转化轮系的传动比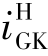可表示为

应用上式时，应注意：

①该公式只适用于齿轮G、K和行星架H的回转轴线重合或平行。

②应视G为起始主动轮，K为最末从动轮，中间各轮的主从地位应按这一假定在转化轮系中去判断。

③等号右侧的“±”的判断方法同定轴轮系。如果只有平行轴圆柱齿轮传动，可由（-1）m来确定。如果含有圆锥齿轮传动或蜗杆传动，则用画虚箭头的方法来确定。若齿轮G和K的箭头方向相同时为“+”，相反时为“-”。

④代入各个构件实际转速时，必须带有“±”。可先假定某一个已知构件的转向为正向，其他构件的转向与其相同时取“+”，相反时取“-”。

例7.3　如图7.11（a）所示的周转轮系中，已知齿轮齿数z1=40，z3=60，两中心轮同向回转，转速n1=100r/min，n2=200r/min，求行星架H的转速nH。

解：由式（7.2）得(https://www.xing528.com)

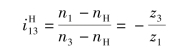
齿数比前的“-”表示在转化轮系中轮1与轮3转向相反。由题意可知，轮1和轮3同向回转，故n1和n3以同号代入上式，则有

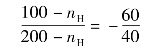
解得

经计算nH为正，故行星架H与齿轮1转向相同。

例7.4　如图7.12所示圆锥齿轮组成的行星轮系中，各轮的齿数为：z1=20，z2=30，z2′=60，z3=80。已知n1=90r/min。求行星架H的转速nH。

解：在该轮系中，齿轮1、3和行星架的轴线重合，所以可用式（7.3）进行计算

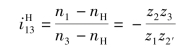
上式等号右边的负号，是由于在转化轮系中画箭头（见图7.12中虚线箭头）后，1、3两轮的箭头方向相反。

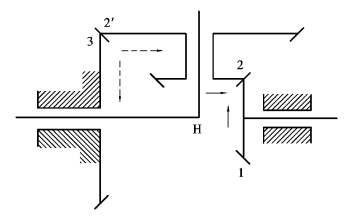
图7.12　周转轮系及其转换轮系

设n1的转向为正，且齿轮3与机架固定，代入得

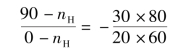
解得

正号表示nH的转向与n1的转向相同。

注意，本例中行星齿轮2和2′的轴线与齿轮1、3及行星架的轴线不平行，所以不能利用公式（7.3）来计算n2。