定轴轮系传动比的计算方法

传动比是指输入轴与输出轴的角速度之比，而轮系的传动比则指轮系中首、末两个构件的角速度之比。轮系的传动比包括传动比的大小和首、末两构件的转向关系两方面的内容。

首先分析最简单的只有一对齿轮的轮系。设主动轮1的转速和齿数为n1、z1，从动轮2的转速和齿数为n2、z2，从前面章节中已知其传动比大小为

圆柱齿轮传动的两轮轴线互相平行，如图7.5（a）所示的外啮合传动，两轮转向相反，传动比用负号表示；如图7.5（b）所示的内啮合传动，两轮转向相同，传动比用正号表示。因此，两轮的传动比可写成

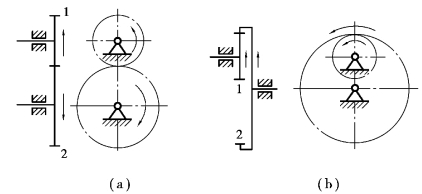
图7.5　一对平行轴圆柱齿轮的转向关系

两轮的转向关系也可在图上用箭头来表示，如图7.5所示，箭头方向表示齿轮可见侧的运动方向。用相反的箭头（箭头相对或相背）表示外啮合时两轮转向相反，同向箭头表示内啮合转向相同。

两圆锥齿轮的轴线相交，其转向关系不能用传动比的正负来表示，只能在图上用箭头表示，根据主动轮和从动轮的受力分析可知，表示两轮转向的箭头必须同时指向节点或同时背离节点，如图7.6所示。

如图7.7所示平面定轴轮系的传动比，齿轮1和2为一对外啮合圆柱齿轮；齿轮2和3为一对内啮合圆柱齿轮；齿轮4和5、齿轮6和7又是两对外啮合圆柱齿轮。设齿轮1为主动轮（首轮），齿轮7为从动轮（末轮），则此轮系的传动比为

图7.6　圆锥齿轮的转向关系

轮系中各对啮合齿轮的传动比依次为

另外，齿轮3和齿轮4同轴，齿轮5和齿轮6同轴，所以n3=n4，n5=n6。

由图7.7可见，主动轮1到从动轮7之间的传动，是通过上述齿轮的依次传动来实现的。因此，为了求得轮系的传动比i17，可将上列各对齿轮的传动比连乘起来，得

图7.7　平面定轴轮系

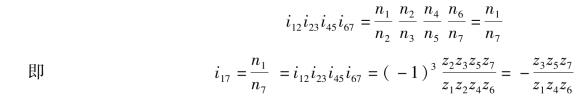(www.xing528.com)

上式表明：

①定轴轮系的传动比大小等于组成该轮系的各对啮合齿轮传动比的连乘积；也等于各对啮合齿轮中所有从动齿轮齿数的连乘积与所有主动齿轮齿数的连乘积之比。

②对于各种定轴轮系，主动轮与从动轮的转向关系都可以用箭头法判定。对于各齿轮轴线相互平行的平面定轴轮系，还可以用符号法判定，具体方法是在齿数比的基础上乘以（-1）m，m为轮系中齿轮外啮合次数。

③齿轮2在轮系中既是从动轮，又是主动轮，这种齿轮称为惰轮。惰轮的齿数对传动比的大小没有影响，但是改变了转向关系。

综上所述，定轴轮系传动比的计算可写成通式：

式中，m为轮系中外啮合的齿轮对数。

例7.1　如图7.7所示轮系中，已知各个齿轮的齿数分别为：z1=30，z2=30，z3=90，z4=25，z5=36，z6=20，z7=45，求轮系的传动比i17。

解：该轮系是一个平面定轴轮系，根据式（7.1）得

经计算，传动比i17为负值，表示齿轮7与齿轮1转向相反。

例7.2　如图7.8（a）所示，已知z1=18，z2=54，z2′=20，z3=80，z3′=21，z4=63，z4′=20，z5=90，若n1=800r/min，求轮5的转速及各轮的转向。

解：该传动系统是由圆柱齿轮和圆锥齿轮组成的空间定轴轮系，由于两圆锥齿轮的轴线相交，其转向关系不能用传动比的正负来表示，只能在图上用箭头表示。

①传动比大小根据式（7.1）计算

②各轮的转向

各轮的转向按画箭头的方法确定，如图7.8（b）所示。

图7.8　定轴轮系传动比计算