计算平面机构自由度的注意事项优化建议：平面机构自由度计算的注意事项

在计算机构的自由度时，如遇到以下几种情况时必须加以注意，否则将会出现结果与机构的实际运动不吻合的情况。

（1）复合铰链

两个以上的构件在同一处以转动副相连接，所构成的运动副称为复合铰链。如图2.15（a）所示，有3个构件1、2、3在A处汇交成复合铰链，图2.15（b）所示为它的俯视图。由图2.15（b）可以看出，这3个构件组成两个转动副。以此类推，K个构件汇交而成的复合铰链有（K-1）个转动副。在计算机构自由度时，应注意识别复合铰链，以免把复合铰链的个数算错。

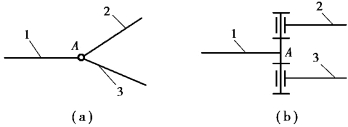
图2.15　复合铰链

例2.4　试计算图2.16所示钢板剪切机传动系统的自由度。

解：由图可知，机构中有5个活动构件n=5，B处是3个构件汇交成的复合铰链，有两个转动副，O、A、C各处分别有一个转动副，滑块5与机架6之间组成一个移动副，故低副个数PL=7，高副个数PH=0。由式（2.1）得机构的自由度

该机构的自由度与原动件数相等，故具有确定的运动。当原动件1转动时，滑块5沿机架6上下移动。

（2）局部自由度

机构中常出现一种与输出构件运动无关的自由度，称为局部自由度或多余自由度，在计算机构自由度时应予以排除。

例2.5　试计算图2.17（a）所示滚子从动凸轮机构的自由度。

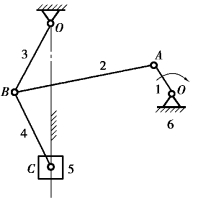
图2.16　钢板剪切机

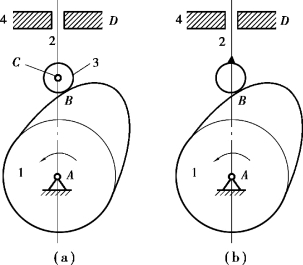
图2.17　局部自由度

解：由图可知，当原动件凸轮1转动时，通过滚子3驱使从动件2以一定运动规律在机架4中往复运动。从动件2是输出构件。不难看出，在这个机构中，无论滚子3绕其轴线是否转动或转动快慢，都不影响输出构件2的运动，因此，滚子3绕其轴线转动，是一个局部自由度，在计算机构的自由度时应排除这个局部自由度，如图2.17（b）所示，设想将滚子3与从动件2焊成一体（转动副C也随之消失）。此时，n=2，PL=2，PH=1。

由式（2.1）得机构的自由度(www.xing528.com)

虽然滚子3的局部自由度不影响整个机构的运动，但它可使高副处的滑动摩擦变成滚动摩擦，减少了磨损，所以实际机械中常有局部自由度出现。

（3）虚约束

在运动副引入的约束中，有些约束对机构自由度的影响是重复的，这种重复而对机构运动不起独立限制作用的约束称为虚约束或消极约束。在计算机构的自由度时应将虚约束除去不计。

虚约束是构件间几何尺寸满足某些特殊条件的产物。平面机构中的虚约束常出现在下列场合：

①两个构件之间组成多个移动副，且导路相互平行或重合时，如不考虑构件的受力，仅从运动方面考虑，其中只有一个移动副起约束作用，其余都是虚约束。如图2.18（a）所示机构的导路平行和如图2.18（b）所示机构的导路重合时，D、E两个移动副中，其中之一是虚约束。

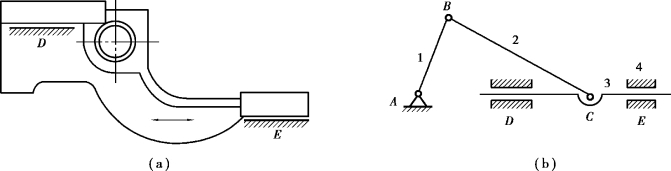
图2.18　移动副虚约束

②两个构件之间组成多个转动副，且轴线重合时，只有一个转动副起约束作用，其余都为虚约束。如图2.19所示，两个轴承支撑一根轴，该机构的A、B两个转动副中，其中之一是虚约束。

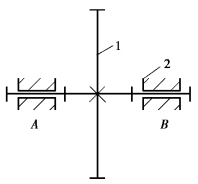
图2.19　转动副虚约束

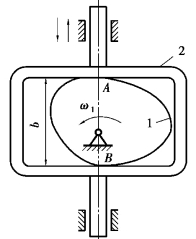
图2.20　高副虚约束

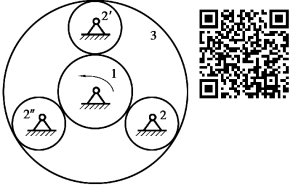
图2.21　对称结构虚约束

③两个构件之间组成多个高副，且各高副接触点处公法线重合时，只考虑一处高副引入的约束，其余都为虚约束，如图2.20所示，该机构中A、B两个高副，其中之一是虚约束。

④机构中对运动不起限制作用的对称部分，其对称部分可视为虚约束。如图2.21所示的行星轮系中，中心轮1通过对称布置的3个完全相同的行星齿轮2、2′和2″驱动内齿轮3，其中有两个行星齿轮对传递运动不起独立作用，是虚约束。此处采用3个完全相同的行星轮对称结构，目的是改善构件的受力。

在实际机构中，虚约束虽对机构的运动不起约束作用，但它可以保证机构顺利运动，增强机构的刚性或改善构件的受力。因此，虚约束的应用相当广泛。在计算机构的自由度时，应认真分析机构中是否有虚约束，如有虚约束，应先除去，然后再进行自由度计算。