优化二维微执行器的拓扑结构

二维微执行器的拓扑优化设计区域如图9.5所示。该问题的设计目标为：当输入力F1作用在设计区域的左侧中点时，输出端要产生与输入力F1方向相反的动作；当输入力F2作用在设计区域的下部中点时，输出端要产生与输入力F2方向相反的动作。当然，输入力的方向和输出端的位移方向还有其他的组合方式。

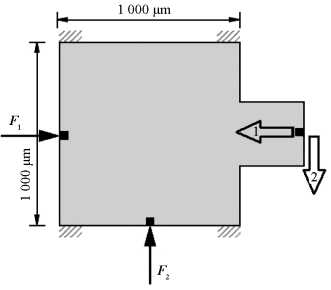
图9.5　二维微执行器的拓扑优化设计区域

这是个多工况优化问题，首先采用第3章柔性机构的互能模型分别建立F1和F2单独作用时的目标函数，需要6个载荷工况，如图9.6所示，其中FV是虚拟的单位载荷。

当F1单独作用时，计算互能模型的目标函数需要图9.6（a）～图9.6（c）所示的载荷工况。

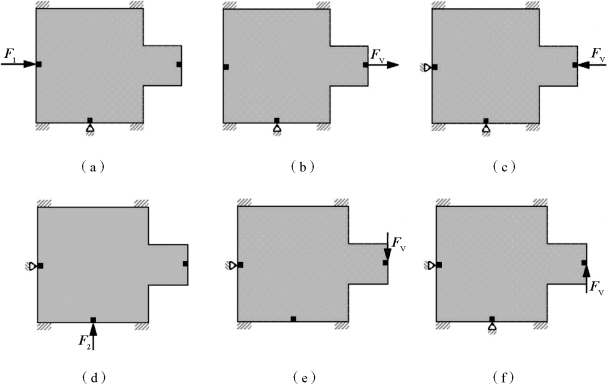
图9.6　计算二维微执行器所需的载荷工况

（a）工况1；（b）工况2；（c）工况3；（d）工况4；（e）工况5；（f）工况6

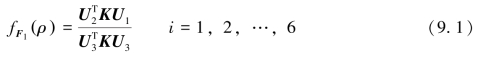
式中，K为整体刚度矩阵；Ui为各工况下的节点位移阵；Fi为各工况下的节点载荷阵。

同理，当F2单独作用时，计算互能模型的目标函数需要图10.6（d）～图10.6（f）所示的载荷工况。

这样二维微执行器优化问题的目标函数就是式（9.1）和式（9.2）的加权和，权因子是根据各工况的贡献大小来决定的。对于本问题而言，二者同样重要，因此，权因子ω1和ω2都取0.5，其拓扑优化的数学模型为

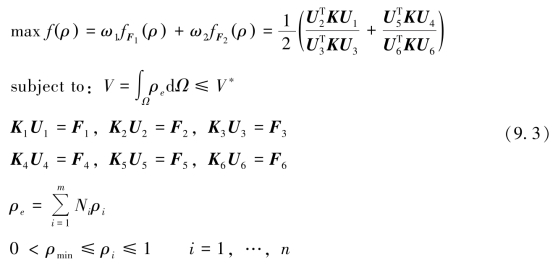(www.xing528.com)

此问题所用材料是电铸镍，其弹性模量为E=200 GPa，泊松比ν=0.31，体积约束为30%。采用节点密度法得到的拓扑优化结果如图9.7（a）所示，对其二值化处理后的拓扑优化结果如9.7（b）所示。

图9.7　二维微执行器的拓扑优化结果

（a）采用节点密度法得到的；（b）二值处理后的结果

采用有限元方法计算二值化处理后的模型在各工况下的位移结果，如图9.8所示。

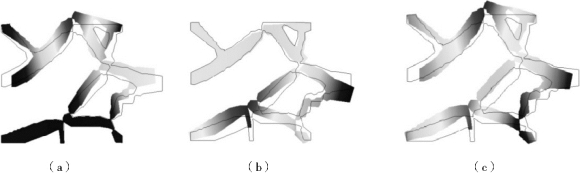
图9.8　在各工况下的位移结果

（a）单独施加F1的位移结果；（b）单独施加F2的位移结果；（c）F1和F2共同作用的位移结果

本书设计的二维微执行器以电热式V型致动器作为驱动源，其结构示意图如图9.9所示，它是利用V型悬臂梁在两端电极施加电压负载后，电流流经V型悬臂梁时产生焦耳热，导致V型悬梁因热膨胀而伸长，使得V型悬臂梁尖端往前变形产生位移。一般电热式V型致动器大多使用硅作为结构材料，但本书的电热式V型致动器所用材料是镍，因镍具有较大的电阻系数、热膨胀系数与较小的热传导率，所以在电热变形上有较好的表现。采用6个V型悬臂梁串联的组合形式可以获得较大的输出力。

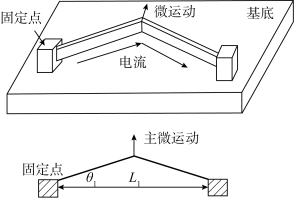
图9.9　电热式V型致动器结构示意

最后，本书以拓扑优化结果为基础，综合考虑工艺流程等因素的影响，得到了该二维微执行器的整体结构形式，如图9.10所示。

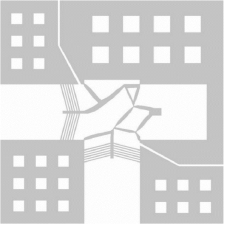
图9.10　二维微执行器的整体结构形式