弹性热应力有限元方程求解

当物体内部温度发生变化时，物体由于热变形将产生线应变α（φ-φ0），其中α是材料的线膨胀系数，φ是弹性体内任一点当前的温度值，φ0是初始温度值。如果物体各部分的热变形不受任何约束，则物体发生变形将不会引起应力。但是如果物体受到约束或者各部分的温度变化不均匀，使得物体的热变形不能自由进行时，则会在物体中产生应力，即热应力。如果知道弹性体内部的温度场，就可以求出弹性体各部分的热应力。

物体由于热膨胀只产生线应变，而剪切应变为0。这种由于热变形产生的应变可以看作是物体的初应变ε0。对于二维问题，ε0的表达式[110]为

ε0=α(φ-φ0)T　(7.1)

式中，α是材料的线膨胀系数；φ0是物体的初始温度场；φ是物体的稳态或瞬态温度场。φ可由单元节点温度φi通过插值求得，即

式中，Ni是单元的形函数。在物体中存在初应变的情况下，应力与应变的关系可表示成如下。

根据虚位移原理[507]，有

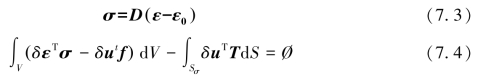
可得到包括温度应变在内的用于求解热应力问题的最小位能原理，它的泛函表达式（其中为温度T的共轻矩阵）为

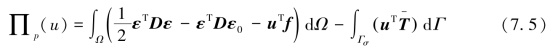
将求解域Ω进行有限元离散，从δ∏p=Ø，将可得到有限元求解方程为(www.xing528.com)

KU=F　(7.6)

与不包含温度应变的有限元方程相比，载荷向量F中包括了由温度应变引起的温度载荷项为

F=Ff+FT+Fε0　(7.7)

式中，Ff、FT分别是体积载荷和表面载荷引起的载荷项；Fε0是温度应变引起的载荷项，即

式中，B，D分别是应变矩阵和弹性矩阵，对于平面应力问题，应变矩阵B的分块矩阵Bi和弹性矩阵D的表达式分别为

式中，E是材料的弹性模量；ν是泊松比。

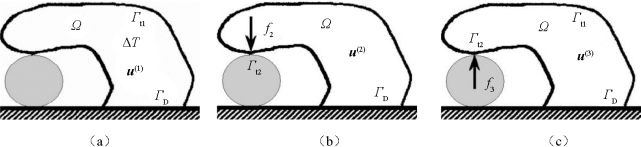
图7.2　微热致动器拓扑优化问题的载荷工况

（a）工况1；（b）工况2；（c）工况3