1.设计目标
简化的INTELSAT-Ⅲ卫星舱布局设计问题可描述如下[441]:在如图6.1(a)所示的INTELSAT-Ⅲ卫星舱内,设置有两个大小相同的垂直于舱的中心轴线的圆形隔板,需要装载的仪器、设备称为待布物。要求将给定的n个待布物合理地布置于圆形隔板上下两侧,使得全舱总体布局满足以下技术要求:
(1)各待布物之间不得发生干涉,即互不重叠;
(2)待布物的任何部分不得超出给定的布局空间,即不得与舱体发生干涉;
(3)整个系统的静稳定性误差,即包含所有待布物的全舱实际质心位置与期望位置(如压心)的误差,应小于给定许用值;
(4)整个系统的主惯性夹角误差,即全舱的惯性主轴与星体坐标轴方向的夹角,应小于给定许用值;
(5)整个系统的惯量特性应尽可能优;
(6)整个系统的空间利用率尽可能高。
2.设计变量
根据问题的实际情况,参考我国航天工业标准[442],本章设计参数所在的相关坐标系定义如下(参见图6.1和图6.2):
(1)Oxyz为全局参考坐标系,其中:
O——坐标原点,选在卫星的对接面或安装测量基准面的几何中心上;
z轴——卫星纵向对称轴,发射瞬时向上为正;
x轴——垂直于纵轴平面,发射瞬时指向为正;
y轴——与x轴、z轴构成右手直角坐标系。
应用全局参考坐标系计算卫星的质心坐标、确定各待布物的布局安装位置等。
(2)O′x′y′z′为星体坐标系(卫星舱质心坐标系),其中:
O′——坐标原点,位于卫星的质心处;
z′轴——卫星纵向对称轴,与z轴平行或重合;
x′轴、y′轴——分别与x轴、y轴平行。
卫星质量特性中的转动惯量、惯量积的数值用星体坐标系给出。
(3)O″x″y″z″为计算单元自身坐标系(待布物质心坐标系),其中:
O″——坐标原点,位于各计算单元(待布物)的质心处,一般选在简化的几何图形的形心上;
x″轴、y″轴、z″轴——计算单元的几何对称轴;在一般情况下,z″轴与z轴平行,而x″轴与x轴,y″轴与y轴呈夹角αi(逆时针方向为正)。
计算单元自身坐标系用于求得各待布物相对于其自身轴的转动惯量。
以上各坐标系及其相互间的关系如图6.2所示。
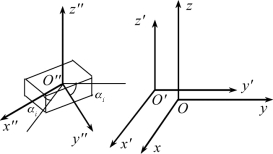
图6.2 各坐标系及其相互间的关系
设待布物集合OBJ={Obj1,Obj2,…,Objn},n为待布物总数。本章中各待布物均简化为质量分布均匀的长方体或圆柱体包围盒。待布物Obji可描述为:Obji(pi,Ψi,di),其中pi=(xi,yi,zi)T∈R3为位置参考点坐标,本章均取质心为待布物位置参考点;Ψi=(α1,βi,χi)T∈R3为Obji在相对于全局参考坐标系Oxyz的三个坐标轴z、x、y的方向角,逆时针为正。di∈R3为待布物的几何尺寸向量。对长方体待布物,di=(ai,bi,hi)T,其中ai、bi、hi分别为底面长、短边长和高度;对圆柱体待布物,di=(ri,0,hi)T,其中ri、hi分别为底面半径和高度。为叙述方便,以下将所有舱体固定件整体视为一个物体,包括舱体壁、圆形隔板和舱内支撑立柱等,记为Obj0。在布局问题中,一般情况下待布物的几何尺寸是已知的,故最终要确定的是待布物的位置参考点位置和放置方向。则一般性卫星舱整体布局方案(设计变量)可表示为
![]()
对于本章中的卫星舱布局问题,由于待布设备安装在圆形隔板上,圆形隔板基面与全局参考坐标系Oxyz的xOy平面平行,因此,对于任意一个待布设备Obji,其相对于坐标轴x、y的方向角βi=χi=0,对圆柱体待布物,αi=0;对长方体待布物,αi为其底面长边与参考平面xOz的夹角,即长方体绕全局参考坐标系Oxyz的z轴旋转的角度,αi∈[0,π]。则本章的卫星舱整体布局方案(设计变量)可表示为(https://www.xing528.com)
![]()
3.数学模型
根据航天器舱的技术性能要求,分析上述设计目标和设计变量的分析,则本章卫星舱布局问题的优化数学模型可描述如下[69]。
求布局方案Xi∈R4n,即
![]()
不干涉条件为
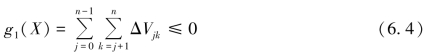
静稳定性(质心位置)误差条件为
g2(X)=|x′-xe|-δxe≤0
g3(X)=|y′-ye|-δye≤0
g4(X)=|z′-ze|-δze≤0 (6.5)
主惯性夹角条件为
g5(X)=|θx|-δθx≤0
g6(X)=|θy|-δθy≤0
g7(X)=|θz|-δθz≤0 (6.6)
上面几个式子中,D为变量Xi可行域;Ixx、Iyy、Izz为全舱(含所有待布物、舱体壁及舱内圆形隔板等其他固定件)对星体坐标系的转动惯量,其计算公式采用我国航天工业标准[442],计算公式为式(6.7)~式(6.9),ΔIxx、ΔIyy、ΔIzz为转动惯量的工程许用值;ΔVjk为待布物j、k的干涉体积,干涉量计算方法见Adamowicz(1976)和ESRO(2007)的文献;O′(x′,y′,z′)为卫星舱质心位置的真实值,(xe,ye,ze)为卫星舱质心位置的期望值,(δxe,δye,δze)为卫星舱质心位置误差许用值,则有
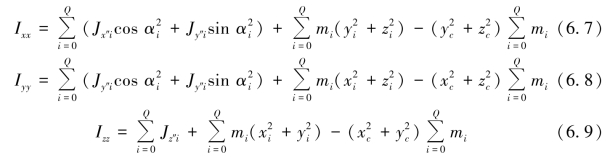
卫星舱的质心坐标可按下式计算,即
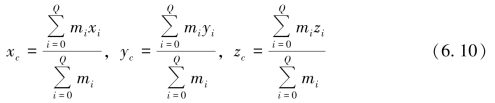
Jx″i、Jy″i和Jz″i分别表示第i个待布物绕其自身坐标系x″轴、y″轴和z″轴的转动惯量,其含义参见图6.3,计算方法如下。
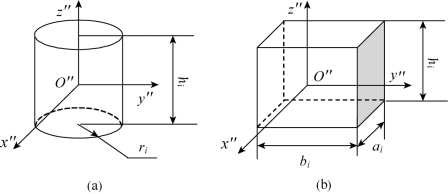
图6.3 待布物在待布物质心坐标系下绕各坐标轴转动惯量的计算
(a)圆柱体待布物;(b)长方体待布物
对于圆柱体待布物i,有
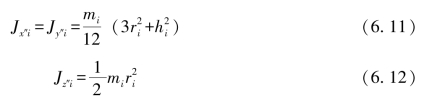
对于长方体待布物i,有
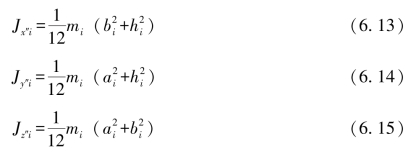
δθx、δθy、δθz为舱体主惯性夹角的许用值,θx、θy、θz分别为舱体惯性主轴与星体坐标系x′、y′、z′坐标轴方向的夹角,计算方法为
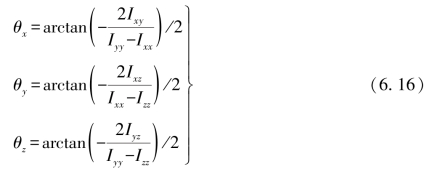
式中,Ixy、Ixz、Iyz为全舱相对于星体坐标系的惯性张量,计算方法为
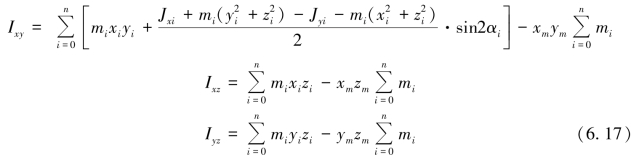
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




