柔性机构的增益模型：机械增益与几何增益的定义与应用

设计机械装置的目的在于把施加的能量转变为最有用的形式，或转变为有效的机械功。输出力和输出位移是评价机构性能的两个最为重要的指标。机构设计中有两个重要概念，分别是机械增益（Mechanical Advantage，MA）和几何增益（Geometrical Advantage，GA）[489]。

机械增益定义为输出力与输入力之比，如图5.3（a）所示，其表达式为

几何增益定义为输出位移与输入位移之比，如图5.3（b）所示，其表达式为

图5.3　柔性机构的机械增益与几何增益

（a）机械增益；（b）几何效益

因此，当设计目标是要求柔性机构具有最大的输出力时，就把机械增益作为目标函数，这时柔性机构具有致动器的功能。反之，当设计目标是要求柔性机构具有最大的输出位移时，就把几何增益作为目标函数，这时柔性机构就是一个理想传递运动的机构。

1.机械增益

假设与柔性机构接触的工件是刚性的，那么柔性机构的输出力可以用其对工件的反作用力表示[如图5.4（a）所示]，即

Uout=-R　(5.22)

因为图5.4所示的三种工况下的位移场属于同一个允许位移空间V={v：v∈H1（Ω），v=0 onΓD}，所以它们的平衡状态方程可由虚功原理[式（5.1）]表达为

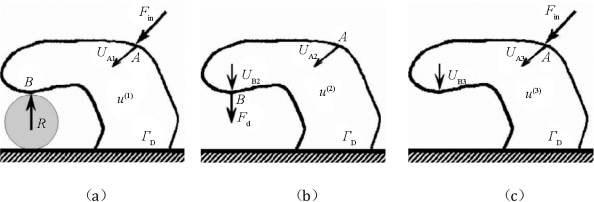
图5.4　计算机械增益所需的载荷工况

（a）工况1；（b）工况2；（c）工况3

对于工况1，设虚位移δu=u（2），则有

α(u(2),u(1))=Fin·UA2+R·UB2　(5.23)

对于工况2，设虚位移δu=u（2），则有

α(u(2),u(2))=Fd·UB2=|UB2|　(5.24)

式中，Fd是个单位载荷，其方向与R相反，所以(www.xing528.com)

R=-|R|Fd　(5.25)

如果设虚位移δu=u（1），则有

α(u(1),u(2))=0　(5.26)

对于工况3，设虚位移δu=u（2），则有

α(u(2),u(3))=Fin·UA2　(5.27)

合并式（5.23）和式（5.26）后，再代入式（5.27）整理得

R·UB2=-α(u(2),u(3))　(5.28)

再由式（5.24）可得工件反作用力大小的表达式为

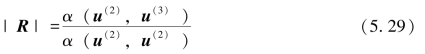
最后，将式（5.29）代入式（5.20）得到机械增益的计算式为

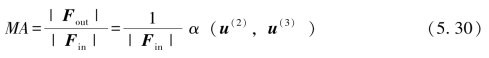
2.几何增益

同计算机械增益的方法类似，对于图5.5（a）和图5.5（b）所示的两种工况，根据式（5.3）可得

α(u(1),u(1))=Fin·u(1)　(5.31)

α(u(2),u(1))=Fd·u(1)　(5.32)

因此几何增益的计算式为

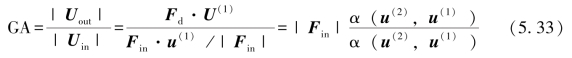
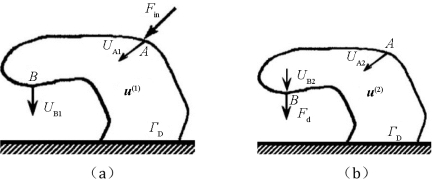
图5.5　计算几何增益所需的载荷工况

（a）工况1；（b）工况2

由上述分析可以看到，互能模型的目标函数式（5.11）与机械增益式（5.30）、几何增益式（5.33）在形式相近，只是具体计算时所考虑的边值条件不同。本章主要采用互能模型求解柔性机构的拓扑优化。