柔性机构的互能模型及载荷分析

柔性机构要具备运动功能，即柔性机构能产生一定的变形以满足其设计目标的运动要求；同时其还要具备结构功能，即柔性机构必须具有一定的刚性，以便把输入端的作用力传递给输出端的物体上。例如，当设计一个微型夹持机构时，为了夹持工件，机构输出端必须要有足够大的输出位移，当柔性机构夹持住工件后，会受到工件的反力，为承受外加载荷，保持其形状不变，机构必须具有一定的刚性。

柔性机构的柔性可采用输入端和输出端之间的互能（Mutual Potential Energy，MPE）来表征。如图5.1所示，弹性体分别受到两个不同载荷作用，但是其他边界条件相同，这意味着这两种工况下的位移场属于同一个允许位移空间V={v：v∈H1（Ω），v=0 onΓD}，它是Hilbert空间的一个闭子集。引入能量公式的双线性形式为

式中，u（i），u（j）∈V是两个允许位移函数。外载荷的线性形式为

α(u(j),u(i))=L(i)u(j)　(5.2)

L(i)(u(j))=∫f(i)·u(j)dΓD　(5.3)

图5.1　柔性机构的互能模型

（a）实际载荷作用于机构；（b）虚拟载荷作用于机构

对于图5.1所示的两种情况，根据虚功原理，如果f1是实际载荷，f2是单位虚拟载荷，则由式5.3可以得到

式（5.4）表示当f1作用在边界Γt1上时，在边界Γt2上沿着f2方向上的变形大小。由式（5.3）可知，双线性形式α（u（1），u（2））=L（1）（u（2））=u（1）|Γt2则是图5.1（a）所示实际载荷在边界Γt2引起的位移测度。因此，式（5.1）可以用于表征柔性机构设计中机构的柔性。实际上这就是互能的表达式，它是由Prager提出的。因此，柔性机构的互能越大说明柔性越大，机构受力作用时越容易产生形变。如果柔性机构的设计要求是当外力f1作用于输入端Γt1处，在输入端Γt2要产生尽可能大位移输出，那么柔性机构的设计目标可表述为

max L(1)(u(2))　(5.5)

由式（5.2），可将式（5.5）改写为

maxα(u(1),u(2))　(5.6)

其有限元离散形式为

式中，U1为f1作用于柔性机构时得到的节点位移阵：U2为f2作用于柔性机构时得到的节点位移阵，K为柔性机构的整体刚度矩阵。

柔性机构的刚性要求，通常采用系统的应变能（Strain Energy）来衡量结构刚度的大小，应变能是指结构受到外加荷载作用发生变形时，系统内部产生的弹性能。为了能够模拟柔性机构受到的反力，采用如图5.2所示工况来计算系统的应变能，其中输入端Γt1处的自由度被约束，输出端Γt2处的作用力f3是与f2方向相反的虚拟载荷。这样柔性机构对刚性的要求为

由式（5.1）可知上式等效为

minα(u(3),u(3))　(5.9)(www.xing528.com)

其有限元离散形式为

图5.2　柔性机构的刚性要求

上述分析可知，柔性机构的运动功能和结构功能是两个相互对立的目标。如果柔性机构的设计只追求输出端形变量，柔性本身可能由于刚性太差而不能承受额定的载荷。相反，若柔性机构的设计为提高传递力而只注重于提高结构的整体刚性，则为达到设计所需的形变量必须施加以较大的输入力，导致机构的效率很低。例如，当设计一个夹持机构时，为接触到工件，构件本身必须产生足够大的形变。当柔性机构接触到工件后，其自身应具有足够的刚性以把输入力传递到工件上。因此柔性机构的设计是一个多目标优化问题，柔性机构的拓扑优化就是找出这两个相互对立要求的最佳平衡点。多目标优化问题的优化结果称为帕累托最优（Pareto Optimum），它对目标函数的表达方式有强烈的依赖性[488]。目前有3种典型的方法用于多目标优化问题的求解：加权法、ε约束法和目标规划法。加权法是将多个目标函数线性组合成一个单目标函数，此方法比较简单，但是各个目标函数的权值不易确定，而且各个目标函数的数值最好在同一量级上。ε约束法是将k个目标中的k-1个目标转化成约束条件，剩余的一个目标作为目标函数。这样就将原问题转化成一个单目标优化问题。同样如何确定适当ε值也是一个很困难的问题。目标规划法是为每个目标定义一个目标值（goal），然后关于这个目标值进行优化，此时的优化过程就相当于单目标优化。

为了能够得到一个合理的Pareto（帕累托）最优解，采用加权法将柔性机构的两个设计目标，即式（5.6）和式（5.9）组合成如下比值形式，即

式（5.11）将柔性机构的柔度和刚度赋予了相同的权值。当需要赋予柔度和刚度不同的权值时，可以采用式（5.12）计算，即

max f=Wlg(α(u(1),u(2)))+(1-W)lg(α(u(3),u(3)))　(5.12)

式中，W是权值。当W=0.5时，式（5.12）和式（5.11）是等效的。实际上对于柔性机构的拓扑优化，式（5.11）是一个自然且合理的选择，因为它平衡了机构的柔度和刚度两方面的要求。因此，基于互能的柔性机构拓扑优化数学模型为

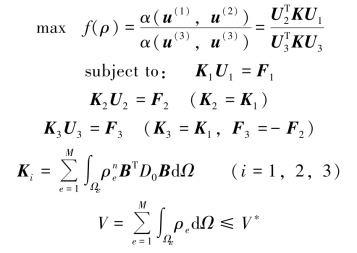
式中，Ki为柔性机构的整体刚度矩阵；Ui为柔性机构的节点位移阵；Fi为柔性机构的节点载荷阵。式（5.13）中目标函数的敏度为

通常情况下，柔性机构的驱动力f1[如图5.1（a）所示]是与设计变量无关的。同样，虚拟载荷f2和f3也是与设计变量无关。由此可得

因此，互能函数关于设计变量的敏度为

同理，应变能函数关于设计变量的敏度为

将式（5.18）和式（5.19）代入式（5.14）即可得到目标函数关于设计变量的敏度。