考题算例与数学模型分析

算例1～算例3（一类已知最优解的带性能约束的圆集packing考题，待布物数量N分别为9、17和25）：算例1～算例3引自黄文奇（1999）的研究成果，是一类以航天器舱布局设计为背景的已知最优解并且带性能约束的packing布局问题（无性能约束的packing由黄文奇给出[411]）。该问题可描述如下：在给定的一个圆形承载板上摆放N个圆形待布物（这里将承载板简化为圆盘，将待布物简化为图元，待布物规模N分别为9、17和25，设圆盘半径R=105 mm，各图元的半径、质心坐标、质量分别为ri，（xi，yi）和mi，具体数据见表4.2。

表4.2　算例1～算例3中待布物的初始数据

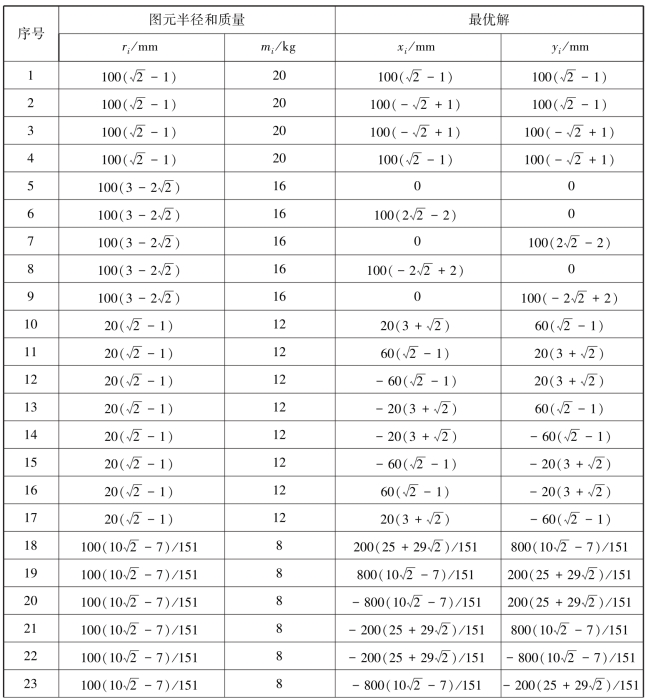
续表

该问题的设计目标为布局空间利用率最大化，要求所有待布物尽量向圆盘中心聚集，即包含所有图元的最小外包络圆半径Rs应尽量小。同时，要求满足下述约束条件：待布物间不发生干涉；待布物与圆盘之间不发生干涉；整体布局的静平衡量小于许用值[δJ]=25 kg·mm。其中，静平衡量为

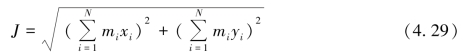
设i，j∈I，i≠j，I={1，2，…，N}，N为圆形待布物的数量，则根据上述布局设计问题建立的数学模型为

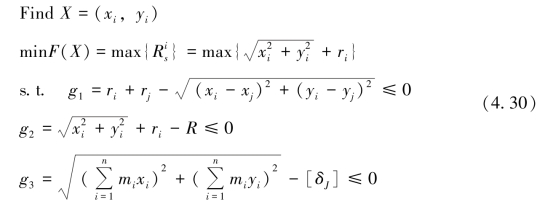
式中，X为各待布物质心位置坐标组成的编码串；g1为待布物间的干涉约束条件；g2为待布物与圆盘间的干涉约束条件；g3为静平衡约束条件；Ris为第i个待布物的外包络圆半径，计算公式为

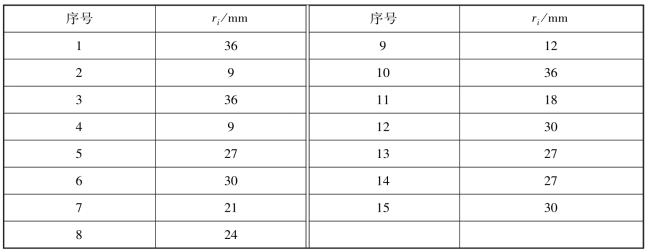
算例4（一类未知最优解的具有邻接位置要求的圆形待布物布局问题，待布物数量N=15）：算例4引自Cahlon（1991）的研究成果。该问题可描述为：在二维布局空间放置N=15个圆形待布物，具体数据见表4.3。设待布物间的权值为ωi，j，ωi，j表示待布物在布局空间中亲密度（或表征距离）的物理量，即ωi，j值越大，两待布物之间越应相互靠近；否则应相互远离。所有待布物形成的权值矩阵W为

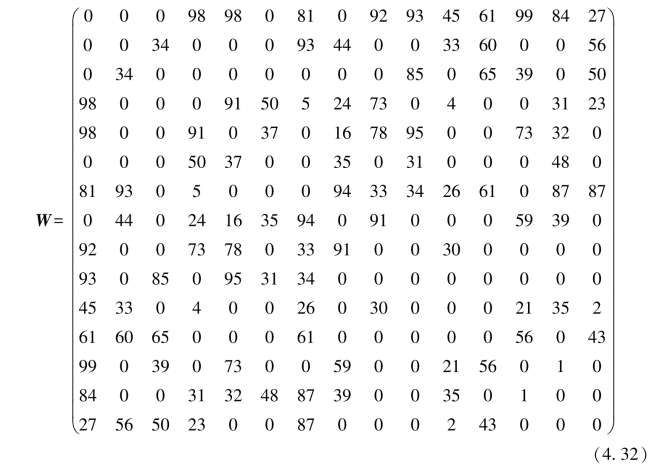
布局设计的目标为：

①加权距离（或权距积）应尽量小，即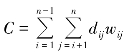的数值应尽量小，亦即权重值较大的待布物应尽量相互聚集，其中dij为两待布物间的距离。

②包含所有待布物的最小外包络矩形面积应尽量小，同时应满足不干涉约束条件，即各待布物之间不发生干涉。

表4.3　算例4中待布物的初始数据

设i，j∈I，i≠j，I={1，2，…，N}，N为待布物的数量，则该布局设计问题的数学模型可描述为(www.xing528.com)

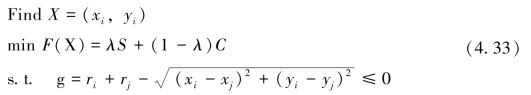
式中，X为问题的解，表示各待布物的质心坐标；S为所有待布物构成的包络矩形的面积；λ为目标间的权重因子；C为权距积，是衡量待布物间邻接位置优劣的物理量；g为待布物间的干涉约束条件。

算例5（一类未知最优解的圆形、矩形待布物混装的带性能约束packing问题，待布物数量N=20）：算例5引自Teng等（2001）的研究成果。该问题可描述为：在一圆形容器内混合放置圆形和矩形待布物，待布物规模N=20。设圆形容器半径R=1 800 mm，矩形待布物12个，可以水平或垂直放置。设矩形长边与x坐标轴的夹角为αi，若水平放置，αi=0；若垂直放置则αi=π/2。圆形待布物8个。设各待布物的质心、质量、长（矩形）、宽（矩形）、半径（圆形）分别为（xi，yi）、mi、ai、bi和ri，具体数据见表4.4。静平衡量的许用值为[δJ]=2.5 kg·mm。该布局设计问题的设计目标和约束条件与算例1～算例3相同，此处不再详述。

表4.4　算例5中待布物的初始数据

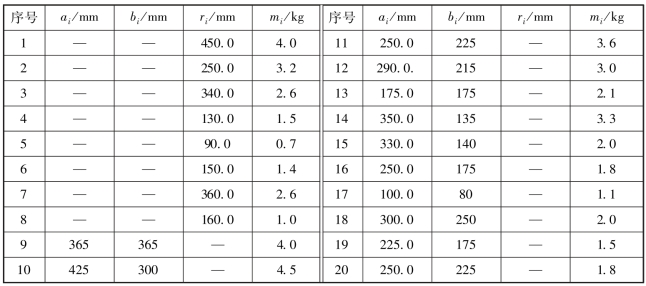
该算例数学模型本质上与算例1～算例3的数学模型一致，只是该算例除圆形待布物外还含有矩形待布物。设i，j∈I，i≠j，I={1，2，…，N}，N为所有待布物数量，则由算例5建立的数学模型为

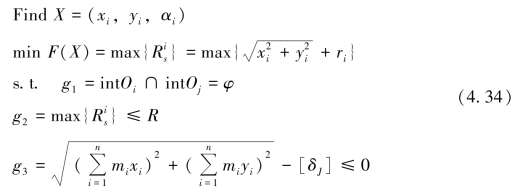
式中，X表示布局问题的解，为各待布物的质心坐标和方向夹角；Oi表示第i个待布物；αi∈[0，π/2]为第i个待布物的方向角，对矩形待布物而言，αi为x轴正方向与矩形长边或其延长线的夹角，逆时针方向为正；圆形待布物的方向角αi为0；g1表示待布物间的干涉约束条件；g2为待布物与容器间的干涉约束条件；g3为静平衡约束条件；为第i个待布物的外包络圆半径。若待布物为圆形，其计算公式同式（4.31）；若为矩形，设矩形i的4个顶点分别为，k=1，2，3，4，代表矩形的各顶点到坐标原点的距离，则为

式中，的计算方法如下。设矩形i各顶点的坐标向量为，矩形i的形心坐标向量为Xi=（xi，yi）T，则

其中，各字母的计算公式为

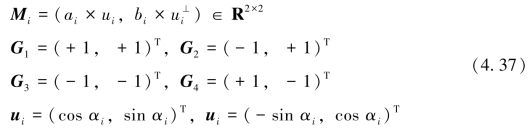
求得矩形i的各顶点坐标后，就可用两点间的距离公式计算的值，从而得出该矩形的外包络圆半径。

至此，为验证本书带启发式协调机制的协同进化算法求解复杂布局设计问题的能力，本书给出了上述以航天器舱布局设计为背景的一组典型测试问题。由其数学模型可知，这类问题实质是一类带性能约束的多目标或单目标优化问题。

目前多目标优化处理方法主要有聚合权重法、目标规划法、按字典顺序优化法、基于Pareto解集法、物理规划法等。对于上述布局算例，以及本书第7章的工程实例问题，本书主要采用工程上常用的聚合权重法将多目标转化为单目标优化问题，关于多目标处理方法的研究非本书重点。本书的具体做法是：以算例4及其数学模型为例，这是一个多目标优化问题，本书将其各子目标函数fi（X）赋予不同的权重系数λi（常数），并将各子目标函数的线性加权作为该问题的评价函数，由此将多目标优化问题转化为单目标优化问题。对约束条件的处理，通常以静态惩罚函数法将其转化为无约束形式，以算例1～算例3为例，原数学模型可转化为无约束形式，即

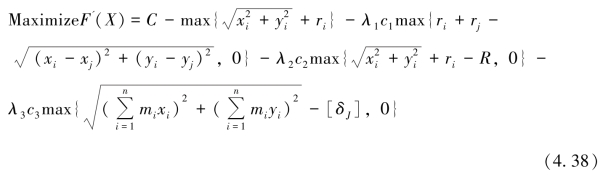
式中，C为常数；λ1、λ2和λ3为各惩罚项的权重（或称为惩罚系数）；c1、c2、c3则代表各项的正规化因子（或归一化因子）。