基于启发式规则的协调机制优化方案

启发式方法基于人类经验建立算法的搜索规则，因此在求解某些特定类型设备布局问题较有效，计算速度较快，可以将人类某些专业领域的经验与计算机相结合，更高效地求解复杂问题。而协同进化算法是以多群体的演化算法为算法基础，因此较易出现在协同进化后期收敛速度慢的缺陷，同时由于协同进化算法首先是将原问题分解为多个子问题，然后进行求解，因此就会出现如何通过多个子问题的求解方案最终确定原问题方案的问题。而针对复杂布局问题，国内外众多学者针对启发式方法求解布局问题进行了丰富的研究，给本书研究启发式方法的启发式协调机制提供很多的参考。基于此，本书研究基于启发式规则的启发式协调机制，主要目的有两个：一是加快各个子问题搜索后期的收敛速度；二是缓解协同进化中各个子问题之间耦合复杂性，确定原问题方案。根据上述目的，本书研究两种启发式方法：基于待布对象的扩展模式局部搜索方法和原问题布局方案的组合-旋转启发式方法。

1.基于待布对象的扩展模式局部搜索方法

相对于传统的确定性搜索方法，演化算法以其隐含的群体并行性、全局性等特点在求解复杂布局问题方面具有一定的优势，但从整体上讲，当布局问题规模较大或者性能约束条件较复杂时，演化算法仍存在早熟、后期收敛速度慢等缺陷，而本书研究的协同进化算法仍然是基于演化算法，因此在算法优化后期，很可能找到一个较优解，仍具有进一步被优化的潜力，但由于演化算法是一种概率性的随机搜索方法，局部搜索能力不强，很难对此较优解进一步优化，而陷入不断的随机搜索过程中，因此会出现后期收敛速度慢的状态，而此时若采用具有局部搜索能力的确定性启发式方法，则有可能进一步快速地发掘此较优解的潜力，使得算法在优化后期快速收敛且保持一定的持续优化能力。

基于上述分析，本书研究基于待布对象的扩展模式局部搜索方法来加强算法的局部搜索能力。Su Yin（2000）研究的求解三维设备布局问题的扩展模式搜索方法对本书提供了很好的借鉴和启发，其中扩展模式搜索方法伪代码如图4.2所示。它对基本模式搜索算法作了以下五点扩展：

（1）待布物和模式方向探索次序随机选择；

（2）正常情况下探索步长逐渐减小，但允许小概率增大以充分搜索解空间；

（3）只有当平移和旋转均无法找到更优解时，尝试待布物位置交换；

（4）搜索方向的构造反映布局问题的特定约束条件；

（5）用于干涉检验的八叉树模型精度随步长动态变化。

将基于待布对象的扩展模式局部搜索方法应用于布局设计问题，计算结果显示，此方法得到相同或相当质量布局方案所需的计算时间比传统的模拟退火算法缩短1～2个数量级，为目前最有效的布局方法之一。本书采用局部搜索方法的目的为：在协同进化搜索后期采用，提高收敛速度；搜索对象是演化子群体中若干个较优的个体，而不是Su Yin（2000）所涉及的单个解；在不改变当前作用的布局方案中待布物之间位置关系的前提下，进行局部搜索。要实现上述的几个目的，完全采用Su Yin（2000）研究的方法是很难实现的，因此，本书基于Su Yin（2000）的扩展模式搜索方法，对其进行如下的几方面的改进：

（1）算法同时对多个解进行搜索，即从群体中选择多个较优的个体，然后采用扩展模式搜索方法同时对这些个体进行局部搜索；

（2）为提高搜索速度，离散化待布物的移动方向且同时对所有待布物进行并行探索；

（3）不进行待布物的旋转和位置交换，以保持当前布局方案中待布物位置关系。

本书将待布物的位置调整离散化为沿有限可行方向以适当步长进行多次移动的过程。以二维布局问题为例，设待布物i当前位置为pi（t）=（xi（t），yi（t））T∈R2，则其下一位置pi（t+1）的候选集合可表示为

图4.2　扩展模式搜索方法伪代码

式中，δi为移动步长。式（4.11）将可行的位置调整限定为以当前位置为中心，在二维平面上以给定步长δi沿均匀分布的q个方向的移动（图4.3所示为8个可移动方向的圆形待布物示意），分别记为方向1、方向2、……、方向q。考虑到待布物i可能选择保持当前位置不变，记为方向0，则每一个待布物下一步可能的位置调整方案共有q+1种。

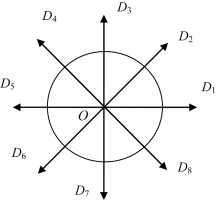
图4.3　8个可移动方向的圆形待布物示意

设具有n个待布物的当前布局方案为LS（t），经一次局部布局模式变换（LLT）得到的布局方案为LS（t+1），即LS（t+1）=LLT（LS（t），e），则该过程可定义为

式中，ei为待布物i的位置调整方向，e=（e1，e2，…，en）T即为布局变换参数。如果式（4.12）中δi是变化的且可以足够小，则任一待布物i经过有限次移动可以以足够的精度进行局部搜索。基于上述待布物位置调整的有限可行方向的定义，可列出本书采用的基于待布对象的扩展模式局部搜索方法伪代码，如图4.4所示。

图4.4　基于待布对象的扩展模式局部搜索方法伪代码

2.原问题布局方案的组合-旋转启发式方法

协同进化中的各个布局子问题协同进化完成之后，下一步是如何根据各个子问题解得到原问题解，由于协同进化中各个子群体仅仅通过几种简单的个体合作方式进行子群体之间协同进化，因此对于具有相互冲突的目标函数和约束条件的复杂布局问题往往出现得到的原问题解虽然逼近优化结束准则但还未达到优化结束准则，尚需进一步优化，而且不能保证各子种群中最好解的合并解是原问题的最好解，例如对于本书的卫星舱布局问题，经常很难同时满足转动惯量、干涉约束和惯性夹角的约束要求，而且对于诸如卫星舱的复杂布局问题，根据工程技术要求的不同，问题的多个优化目标或者约束条件可能存在本质上的串行或者阶段层次的关系，因此若能很好利用此种层次关系，将存在层次关系的约束从原布局问题优化模型中分离出来，进行单独的求解，则一方面可以降低协同进化中子问题之间的目标和约束之间的复杂关系，另一方面可以对原问题的布局方案进行进一步的优化，保持了整体求解的持续优化能力。而孙治国（2000）研究的用于卫星舱布局问题的初始布局的构造的启发式约束魔方变换法为本书提供了很好的启示。

针对上述问题，参考启发式约束魔方变换法[198]，本书提出原问题布局方案的组合-旋转启发式方法来确定最终的原问题布局方案。具体过程主要分为组合和旋转两步。

（1）组合。利用协同进化算法求解得到各个子问题的s个优化布局方案，按照图4.5所示的方式排列，其中第i行第j列元素Xij表示第j个布局子问题的第i个优化布局方案，然后从每一列（即每一个布局子问题的s个优化布局方案）中随机选取一个优化解作为最终布局子方案，经过有限次的上述排列组合，最终从每一个布局子问题中选取一个子布局方案，然后将所有布局子方案组合成为原问题布局方案。对于布局子问题，i选取的最终子布局方案为，则原问题的布局方案X∗可为式（4.13）。

（2）旋转。借鉴启发式约束魔方变换法中的旋转策略[198]，对上述组合之后的布局方案，在保持布局子方案中待布物的相对位置关系的前提下，将各个布局子方案中的所有待布物绕全局自定义坐标系的z轴整体旋转一个角度来调整布局问题约束（如卫星舱的惯性夹角、转动惯量和质心等），得到最后的原问题布局方案，本书中卫星舱布局问题的旋转示意图如图4.6所示。

图4.5　子布局方案组合过程

图4.6　卫星舱布局问题的旋转示意

需要说明的是：本书原问题布局方案的组合-旋转策略中的旋转思想虽然来源于启发式约束魔方变换法中的旋转策略，但两种旋转策略的作用有所不同，启发式约束魔方变换法主要是用来确定卫星舱的初始布局方案，且主要针对某些特殊的承载板进行操作，这些承载板上仅有一个或两个位置固定尺寸较大的、相对于全局参考坐标系x、y轴具有对称几何外形的待布物，本书则是在各个布局子问题协同进化之后，采用原问题布局方案的组合-旋转策略确定原问题布局方案。

设本书采用遗传算法进行原问题布局方案的旋转求解，若具有N个布局子问题，则一旋转方案的编码方式可表示为θ=（θ1，θ2，…，θN），θi∈[-π，π]，该原问题布局方案的组合-旋转策略伪代码如图4.7所示。

如上所述，在求解原问题的布局方案时采用本书给出的基于布局子问题的旋转策略。一方面，可以将整体求解模型分解为两阶段问题，缩小了问题求解规模，如在各个布局子问题进行协同进化求解时，设计变量中可以暂时不考虑待布物的方向变量，等到进行原问题布局方案设计时再考虑；另一方面，通过旋转策略降低了协同进化中子问题之间的目标和约束之间的复杂关系，如在布局子问题进行协同进化求解时可以不用考虑耦合关系较复杂惯性夹角约束，而等到原问题布局方案设计时再考虑，并且由于此旋转策略是对于整个布局子问题的整体旋转，因此可以不用考虑布局子空间内的干涉约束。最后旋转策略还可对组合后的原问题布局方案进行进一步优化，保持整体求解的持续优化能力。为进一步探讨此旋转策略的力学特性，本书以航天器舱布局问题为例，基于旋转策略对航天器舱布局问题的优化目标、约束条件进行重定义，并分析了各个布局子问题之间基于旋转变量的耦合关系，为本书启发式旋转策略的实现奠定基础。

图4.7　原问题布局方案的组合-旋转启发式方法伪代码

3.基于旋转策略的航天器舱布局设计问题重定义及定性关系分析

若具有N个布局子问题，则一旋转方案的编码方式可表示为θ=（θ1，θ2，…，θN），θi∈[-π，π]，θi表示第i个布局子问题所有待布物旋转的角度，设第i个布局子问题中待布物的数量为Qi，书中设逆时针旋转方向为正，由于本书的旋转策略是对布局子问题中包含的所有待布物进行整体旋转，因此在旋转前后各个布局子问题内的待布物之间的相对位置关系保持不变，旋转后第i个布局子问题中待布物j的位置坐标为旋转变量θi的函数，设待布物j的旋转前的初始位置坐标为（xj，yj，1），旋转后待布物j的位置坐标为，则根据计算机图形学的旋转变换关系，有如下的关系，即(www.xing528.com)

则以旋转后可表示为

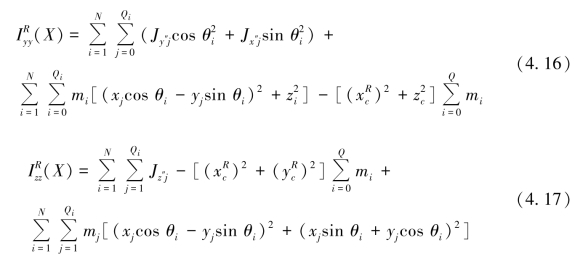
式中，为旋转后系统的质心位置，由于仅绕全局参考坐标系z轴进行旋转，因此旋转前后系统的质心zc不变，质心可按下式计算，即

为了分析旋转前后各个技术性能的变化量，首先计算旋转前后各个技术性能的差异值。对于转动惯量，为方便计算，本书计算旋转前后绕3个坐标轴的转动惯量之和的差异值ΔIR，即ΔIR可表示为

可得到

则旋转前后3个坐标轴惯性积的差异值可表示为

由式（4.21）可以看出，旋转前后转动惯量的差异仅与系统的质心差值有关。转动惯量的大小与待布物自身的转动惯量之和、待布物自身的坐标位置，以及系统的质心位置有关，因此式（4.21）的值的变化范围的数量级相对于系统三个坐标系转动惯量之和的数值很小，即在旋转前后整个系统的转动惯量的数值仅发生较小的变化，即本书的旋转策略对详细设计阶段得到的整体方案的优化目标数值（转动惯量的大小）几乎不产生影响，在接下来的数值实验中也进一步验证了上述想法。

同理，由式（4.22）可以看出，旋转前后惯性积的变化量大小不仅与系统的质心位置有关，而且与待布物的位置、待布物自身的转动惯量有关，同时根据经验，对于本书构型的航天器来说，惯性积的数量级一般很小，而旋转前后惯性积的变化量大小与其计算公式中的每一项都有关系，因此，在旋转前后惯性积的变化量相对于本身的数量级将发生较大的变化，所以本书的旋转策略对整个系统的惯性积的大小影响很大，同样本书将进行数值实验来验证上述的想法。

可以看出，航天器舱布局问题的惯性夹角约束与系统的转动惯量、惯性积的大小有关，通过上述分析，本书的旋转策略可以在不改变系统转动惯量大小的前提下，通过改变惯性积的大小来调整系统的惯性积夹角的大小，并最终在不改变系统优化目标大小的前提下，使得惯性夹角满足要求。

为进一步验证本书的旋转策略，进行如下的数值实验，选取20个详细设计阶段得到的原问题布局方案，作为研究对象，对这些布局方案中的布局子问题进行旋转测试，研究此旋转对整体布局方案的各个技术性能的影响，本书分别进行两个数值测试：一是仅对布局方案中的一个布局子问题中的所有待布物绕参考坐标系的z轴进行整体旋转；二是对布局方案中的两个布局子问题中的所有待布物绕参考坐标系的z轴进行整体旋转。测试的旋转范围为[0，2π]，测试一中转动惯量、惯性积、惯性夹角变化曲线如图4.8、图4.9、图4.10所示。测试二中转动惯量、惯性积、惯性夹角变化曲线如图4.11、图4.12～图4.13所示。

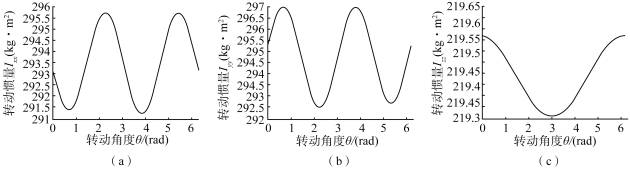
图4.8　测试一中转动惯量变化曲线

（a）转动惯量Ixx；（b）转动惯量Iyy；（c）转动惯量Izz

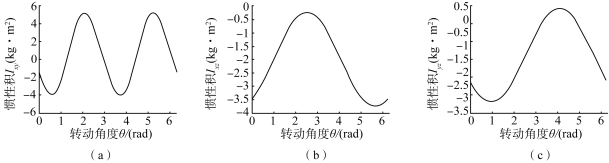
图4.9　测试一中惯量积变化曲线

（a）惯量积Ixy；（b）惯量积Ixz；（c）惯量积Iyz

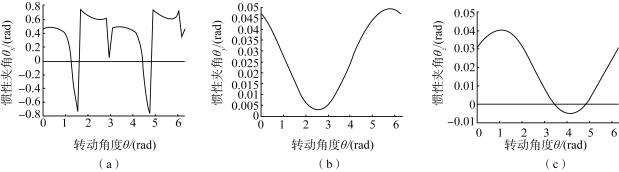
图4.10　测试一中惯量夹角变化曲线

（a）惯量夹角θx；（b）惯量夹角θy；（c）惯量夹角θz

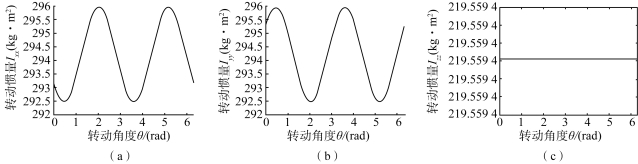
图4.11　测试二中转动惯量变化曲线

（a）转动惯量Ixx；（b）转动惯量Iyy；（c）转动惯量Izz

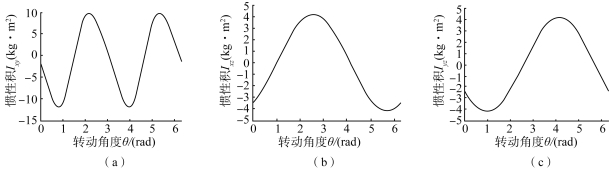
图4.12　测试二中惯量积变化曲线

（a）惯量积Ixy；（b）惯量积Ixz；（c）惯量积Iyz

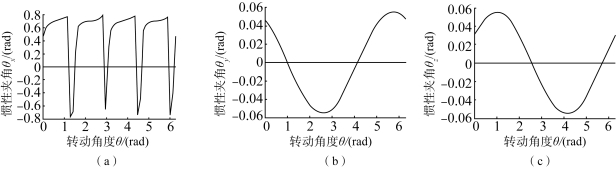
图4.13　测试二中惯量夹角变化曲线

（a）惯量夹角θx；（b）惯量夹角θy；（c）惯量夹角θz

由图4.8～图4.13可以看出，对于本书的两个数值测试，在旋转过程中，转动惯量Ixx的最大变化范围为291.5～295.7 kg·m2，变化量数值占转动惯量Ixx的比率为δ=[（295.7-291.5）/295.7]×100%=1.42%；转动惯量Iyy的最大变化范围为292.5～297 kg·m2，变化量数值占转动惯量Iyy的比率为δ=[（297-292.5）/297]×100%=1.52%；转动惯量Izz的最大变化范围为219.3～219.57 kg·m2，变化量数值占转动惯量Izz的比率为δ=[（219.57-219.3）/219.57]×100%=0.12%；惯性积Ixy的最大变化范围为-12～10 kg·m2，变化量数值占惯量积Ixy的比率为δ=[（10+12）/12]×100%=183.33%；惯性积Ixz的最大变化范围为-4～4 kg·m2，变化量数值占惯量积Ixz的比率为δ=[（4+4）/4]×100%=200%；惯性积Iyz的最大变化范围为-4～4 kg·m2，变化量数值占惯量积Iyz的比率为δ=[（4+4）/4]×100%=200%；惯性夹角θx的最大变化范围为-0.75～0.75 rad，变化量数值占惯量夹角θx的比率为δ=[（0.75+0.75）/0.75]×100%=200%；惯性夹角θy的最大变化范围为-0.05～0.05 rad，变化量数值占惯量夹角θy的比率为δ=[（0.05+0.05）/0.05]×100%=200%；惯性夹角θz的最大变化范围为-0.05～0.05 rad，变化量数值占惯量夹角θz的比率为δ=[（0.05+0.05）/0.05]×100%=200%。

从对比中可以看出，在各个布局子问题旋转的过程中，整个系统的转动惯量数值变化很小，仅为其本身量值的1%左右，而整个系统的惯性积、惯性夹角数值变化量很大，最大变化量可达到本身量值的200%，即本书的旋转策略对整个系统的转动惯量的影响很小，而对惯性积、惯性夹角的影响很大，与上述定性分析的想法相一致。因此，可以在原问题布局设计阶段采用本书的旋转策略在不改变系统优化目标数值的前提下（转动惯量），快速调整惯性夹角的约束。

当然，也可以在详细布局设计阶段在优化待布物位置时考虑待布物的旋转方向，而本书的旋转策略是在详细设计阶段不考虑待布物的旋转方向，而在原问题设计时通过旋转策略整体对各个布局问题中的待布物进行旋转来调整惯性夹角要求，相对于在详细设计阶段考虑待布物旋转方向的方法，本书的方法具有以下特点：

①由于可以在详细设计阶段不考虑待布物的旋转方向，因此可降低详细设计阶段变量的维数；

②由于本书旋转策略可以调整系统的惯性夹角的约束，因此可以在详细设计阶段不考虑惯性夹角的约束要求，缓解了详细设计阶段优化目标与约束之间的冲突，降低了详细设计阶段问题求解困难；

③本书的旋转是对布局子问题中的所有待布物进行整体旋转，因此待布物之间的相对位置不发生变化，在进行旋转时可以不必进行待布物之间的干涉计算，这缩短了旋转策略的计算时间；

④本书的旋转策略可以在不改变详细设计阶段优化目标大小的前提下，对系统的惯性夹角进行快速调整；

⑤本书给出的这种组合-旋转策略仅适用于求解具有多个承载板的航天器舱布局设计问题，并不适用于求解仅有一个承载面的航天器舱布局设计问题。