改进满意度函数的方法

各性能指标的相同偏好区间的满意度设定为相同值的情况下，满意度函数曲线A到B所代表的性能指标间折衷态度的差异，体现为对应偏好区间的改变。其改进策略为：若决策者愿意接受某性能指标d=d0时的不利或有利结果，则减小或增大s（d0）的值。如图3.4所示，在偏好区间满意度不变的情况下，性能指标d的满意度函数形式由s（d）改变为s′（d）代表了dp相对重要性的整体增加。比较s′（d）和s（d）的偏好区间可知，较满意区间范围增大，而较不满意的区间减小。此时，性能指标间的折衷关系体现为各偏好区间比例的变化。

图3.4　满意度函数间的折衷关系

根据这一规律，可构造反映性能指标间的折衷关系的偏好区间比例。若已知各性能指标的权重系数为wp，定义折衷系数为

设由（q-1）个区间组成的整个偏好区间长度为L，一般以性能指标理想的最好解和最劣解为偏好区间边界值t1和tq，有

令

(www.xing528.com)

对进行规范化处理，得到各偏好区间的长度，即

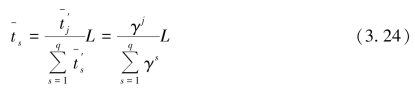
则各偏好区间的边界值可表示为γ的函数，对单调增型满意度函数为

可以证明，γ=1表示决策者对该性能指标持中立的折衷态度，由ts确定的满意度函数s（d）可表示为曲线A；当γ＞1时，s（d）可表示为曲线B；当γ＜1时，s（d）可表示为曲线C。性能指标间的相对重要程度越显著，所建满意度函数的非线性程度越高。若决策者无法给出确定的权重值，折衷系数γp可通过性能指标间相对重要性比例尺度换算。双目标满意优化问题中，性能指标重要性与折衷系数的关系如表3.1所示。

表3.1　性能指标重要性与折衷系数的关系

经过上述改进，满意优化模型的折衷系数为γp，不同γp代表了决策者对性能指标间折衷性能的偏好。