利用偏好区间构造满意度函数的具体方法

物理规则的偏好函数是利用偏好区间边界值进行分段样条曲线拟合建立的，该方法的特点是：仅需较小偏好信息量即可构造非线性函数形式，在数学处理上比较容易；与决策者主观设定的线性函数形式相比，更接近决策者真实偏好结构。对于决策者能够给出几个可能目的值满意度的情况，因此可基于该建模思想构造满意度函数。

对于多目标优化问题，给定性能指标dp的一组满意程度区间边界值tpj，j=1，2，···，q及其对应的满意度函数值spj，spj∈[0，1]，其中，sp1=1，spq=0。令

设

则第s段满意度函数的表达式为

式中，a、b、c、d的取值范围与βj值有关，详细推导公式参见文献（Messac，2002）。

以单调增函数为例，上述方法建立的满意度函数的形式如图3.2所示。

图3.2　基于偏好区间的满意度函数的不同形式

对于相邻两段满意度函数，若恒有kpj=kp，j-1时，为A曲线；kpj＜kp，j-1时，为B曲线；kpj＞kp，j-1时，则属于C曲线；D曲线为B、C形式曲线的组合。决策者能够提供的已知点数tpj越多，满意度函数形式越接近决策者的真实偏好结构。kpj（0＜kpj＜1）的取值与各满意区间边界值及其满意度函数值有关，基于满意区间的满意度函数的结构控制参数向量为（tpj，Spj）。其中，tpj值的物理意义明确，决策者可根据实际情况设置；Spj值可通过对模糊语义进行量化来确定。

当所有性能指标的满意度函数形式均给定后，各性能指标间的折衷关系也随即确定。图3.2中各曲线所表示的决策者折衷态度如下：(www.xing528.com)

（1）曲线A：该满意函数与满意解呈线性关系，表示决策者对性能指标持中立态度，或是认为该决策的后果对大局没有重大影响，或是认为该决策可以重复进行，从而获得平均意义上的成果。因此，不必对决策的某项不利后果特别关注。

（2）曲线B：满意解改进增量与其满意度增量的关系，和满意解在可行区间的位置有关。某性能指标在较优区间的改进被认为对综合性能的提高贡献较大。

（3）曲线C：某性能指标在较差区间的改进被认为对满意解综合性能的提高贡献较大。

（4）曲线D：是曲线B、C的组合，表明不同环境下决策者心态的改变。

曲线B、C、D与曲线A间偏离的大小表明性能指标间的折衷程度。

综上所述，上述方法建立的满意度函数的控制参数向量（tpj，Spj）的不同取值即代表决策者对各性能指标的满意偏好，也体现了其对满意解间的折衷偏好。因此，当（tpj，Spj）值确定后，决策者无须再提供性能指标间的权重信息。与常见满意度函数形式[见式（3.7）～式（3.12）]相比，（tpj，Spj）的取值符合决策者的思维特点，易于工程设计人员使用。

基于偏好区间的满意优化设计过程如下。

（1）建立满意程度区间语义集，根据决策者给定的语义规则建立各满意程度区间到论域U=[0，1]的映射，确定各偏好区间边界值的满意度。

（2）设定各偏好区间边界值，计算各区间边界上的满意度的一阶导数，分段样条曲线拟合获得整个性能指标取值范围上的满意度函数。

（3）考虑各性能指标间的折衷关系，建立综合满意度函数。当各性能指标满意度对应的偏好区间基于相同语义规则确定时，各性能指标满意度可采用物理规划方法集结。设各性能指标的满意度函数为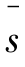（dp），综合满意度函数为s（d），则

（4）建立多目标满意优化模型，进行优化计算，得到最满意设计方案。